数据仓库建模(数据立方体和三种模式)
1.数据立方体(data cube)
(1)常用概念
数据立方体:数据立方体允许以多维对数据建模和观察。实际是N维结构,可以简单看做3-D集合结构
维:一个单位想要记录的透视或者实体
例如:一个数仓sales记录商店的销售设计维time、item、branch和location
维度表:每个维都可以有一个与之相关联的表,里面会有相关的属性(字段)该表称作维表,用来描述维,
基本方体(base cuboid):存放最低层汇总的方体
顶点方体:(apex cuboid)存放最高层的汇总,通常用all标记
举例:
二维:温哥华每个季度(Q1—Q4)的产品销量
三维:多个城市每个季度的产品销量
四维:再在上面维度基础上添加一个维度
2.星形、雪花形和事实星座(多维数据模型)
最流行的数仓模型是多维数据模型。分为星形模式、雪花模式和事实星座模式(1)星形模式
星形模式:(star schema)最常见,数仓包括两部分
一个大的中心表(事实表):包含大批数据并且不含冗余;一
组小的附属表(维度表):每维一个(类似是主表的一个属性)这个模式像星光四射,维表显示在围绕中心表的射线上。
这种模式图很像星光四射,维度表显示在围绕中心表的射线上。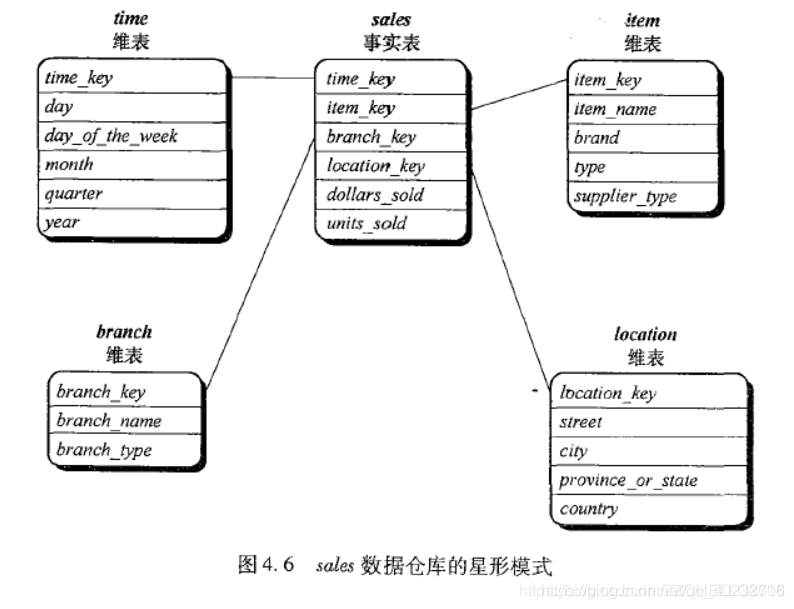
【注意】
在星形模式中,每个维只能用一个表表示,而每个表包含一组属性。这种限制可能造成某些冗余。
(2)雪花模式(snowflake schema)
雪花模式:是星形模式额变种星形模式的某些维表被规范化,把数据进一步分解到附加表中。类似于雪花形状
雪花模式和星形模式的区别:
维度表可能是规范化形式,以便减少冗余。这种表易于维护,并节省存储空间。
由于执行查询需要更多的连接操作,雪花结构可能降低浏览的效率。影响系统的性能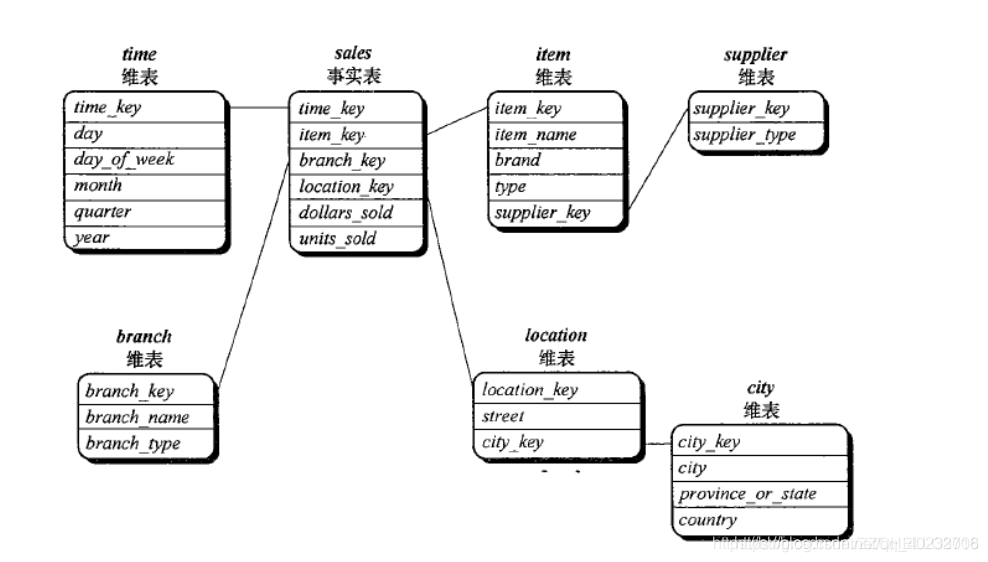
(3)事实星座
事实星座(星系模式):负载的应用可能需要多个事实表共享维表。可以看做是星形模式的汇集
【总结】:在建立数仓式,数仓和数据集市之间是有区别的。
数仓收集了关于整个组织的主题信息(例如:顾客、商品、销售、资产和员工),因此是企业范围的;数仓通常使用星座模式,这样可以对多个相关的主题建模。
数据集市是数仓的一个部门子集,他针对选定的主题,因此是部门范围的。通常采用星形或者雪花模式,更适合对的那个主题建模。
3.维:概念分层的作用
概念分层定义一个映射序列,将低层概念集映射到较高层,更一般的概念。概念分层可以由系统用户、领域专家、知识工程师人工提供或者根据数据分布的统计分析自动的产生。
4.度量的分类和计算
数据立方体空间的多维点可以用‘维-值对’的集合来定义(例如:time=“Q1”,location=“温哥华”,item=“计算机”)
数据立方体度量(measure)是一个数值函数,该函数可以对数据立方体的空间的每个点求值。
通过对给定点的各‘维-值对’聚集数据,计算改点的度量值。
度量根据其所用的聚集函数可以分成三类:
(1)分布的:
一个聚集函数如果能用如下分布方式进行计算,则它是分布的:
假设数据被划分为n个集合,将函数用于每一部门,得到n个聚集值。如果将函数用于n个聚集值得到的结果与将函数用于整个数据集(不划分)得到的结果一样,则该函数可以用分布方式计算。
例如:对于立方体,sum()可以分布计算:首先将立方体划分成子立方体划分成子立方体的集合。对每个子立方体计算sum(),然后对这些子立方体得到的值求和,因此sum()是分布聚集函数。同理count(),min(),max()也是分布聚集函数。
(2)代数的:一个聚集函数如果能够用一个具有M个参数的代数函数计算(其中M是有界正整数)
而每一个参数都可以用一个分布聚集函数求得,则它是代数的。例如avg()可以用sum()/count()计算。
(3)整体的:一个聚集函数 如果描述它的子聚集所需要的存储灭有一个常数界,则它是整体的。也就是说,不存在一个具有M个参数的但是函数进行这一计算。一个度量如果是由整体聚集函数得到的,则它是整体的。
大部分数据立方体需要有效的计算分布的和代数的,相比直线有效的计算整体度量是比较困难的。5.典型的OLAP操作
上卷(上钻):沿一个维的概念分层向上攀登或者通过维归约在数据立方体上进行聚集。street<city<province<country
下钻:上卷的逆操作,它由不太详细的数据到更详细的数据。day<month<quarter<year
切片和切块(slice;dlice):切片操作在给定的立方体的一个维上进行;切块在两个或者多维进行
转轴:转轴是一种目视操作,它转动数据的视角,提供数据的替代表示。
其他OLAP操作
钻过:执行多个事实表的查询
钻透:操作使用关系SQL机制,钻透到数据立方体的底层,到后端关系表