相关性分析
相关分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个因素的的相关密切程度,相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。
1、 如何利用相关系数判断数据之间的关系
(1) 绘制散点图
判断数据是否具有相关关系,最直观的方法就是绘制散点图
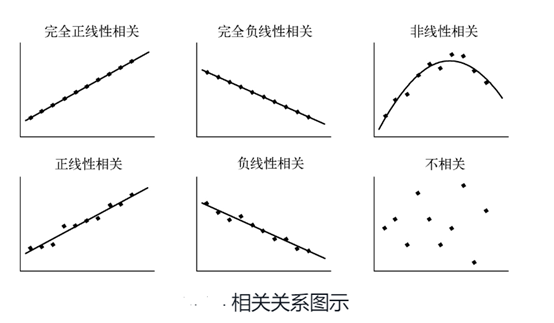
如何要判断多个数据的之间的关系,散点图的绘制就会显得比较繁琐,这时候要选择绘制散点矩阵
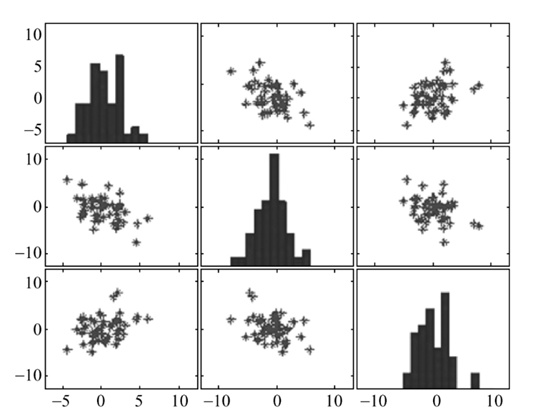
(2) 相关系数
相关系数衡量了两个变量的统一程度,范围是-1~1,‘1’代表完全正相关,‘-1’代表完全负相关。
比较常用的是Pearson‘皮尔逊’相关系数、Spearman‘斯皮尔曼’相关系数。
a) Pearson相关系数
也称皮尔森积矩相关系数,一般用于分析,两个连续变量之间的关系,是一种线性相关系数,公式为:

补充:
|r|<= 0.3 不存在线性相关
0.3<=|r|<= 0.5 低度线性关系
0.5<=|r|<= 0.8 显著线性关系
|r| > 0.8 高度线性关系
b) Spearman相关系数
Pearson相关系数要求连续变量的取值服从正态分布,不服从正态分布的变量、分类或等级变量之间的关联性可采用Spearman秩相关系数,也称等级相关系数来描述。公式:
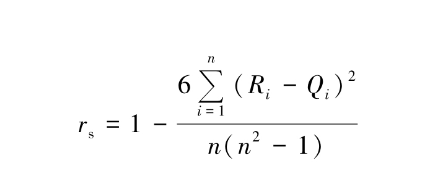
对两个变量成对的取值分别按照从小到大(或者从大到小)顺序编秩,Ri代表xi的秩次,Qi代表yi的秩次,Ri-Qi为xi、yi的秩次之差。
在实际应用计算中,上述两种相关系数都要对其进行假设检验,使用t检验方法检验其显著性水平以确定其相关程度。研究表明,在正态分布假定下,Spearman秩相关系数与Pearson相关系数在效率上是等价的,而对于连续测量数据,更适合用Pearson相关系数来进行分析。
3)判定系数。
判定系数是相关系数的平方,用r2表示;用来衡量回归方程对y的解释程度。判定系数取值范围:0≤r2≤1。r2越接近于1,表明x与y之间的相关性越强;r2越接近于0,表明两个变量之间几乎没有直线相关关系。
2、 应用场景
(1) 利用相关系数来发觉数据间隐藏的联系。
经典相关分析案例是‘啤酒与尿不湿的故事’,这是大家耳熟能详的分析案例了。因为啤酒与尿不湿呈现了明显了正相关性,改变了超市的摆货策略。
但是,这个只是用来说明的案例,在实际中并不存在,尿不湿属于婴儿产品,啤酒属于酒类,没有超市会摆放在一起。在理解相关性分析同时,也要注意现实中的实际情况。现在还有很多书中在引用这个案例,希望大家警惕这样的案例。
(2) 利用相关系数来减少统计指标。
当业务指标繁杂,叙述笼统,给报告制作,分析解读带来巨大的成本的时候。根据相关系数删减指标是方法之一,一般来说相关性大于0.8的时候可以选择其一。
也请大家注意‘相关性’与‘因果性’之间的区别,这两者很容易混淆。在报告中一定要说明情况,避免带来错误的决策。
(3) 利用相关系数来挑选回归建模的变量。
在建立多元回归模型前,需要解决把那些数据放入模型作为自变量。最常规的方式就是先计算所有字段与因变量的相关系数,把相关系数较高的放入模型。然后计算自变量间的相关系数。若自变量间的相关系数高,说明存在多重共线性,需要进行删减。
(4) 利用相关系数来验证主观判断,这或许是现实业务中最有使用必要的。
决策层或者管理层经常会根据自己的经验,主观地形成一些逻辑关系。最典型的表述方式就是“我认为这个数据会影响到那个数据”。到底有没有影响?可以通过计算相关系数来判断。相关系数的应用能够让决策者更冷静,更少地盲目拍脑袋。虽然相关系数不能表达因果关系,但有联系的两件事情,一定会在相关系数上有所反映。
3、代码详解
'''
# 图示初判 散点图
# (1)变量之间的线性相关性
# 创建三个数据:data1为0-100的随机数并从小到大排列,data2为0-50的随机数并从小到大排列,data3为0-500的随机数并从大到小排列
data1 = pd.Series(np.random.rand(50)*100).sort_values()
data2 = pd.Series(np.random.rand(50)*50).sort_values()
data3 = pd.Series(np.random.rand(50)*500).sort_values(ascending=False)
#可知data1与data2呈正线性相关,data1与data3呈正线性相关
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(data1,data2)
plt.grid(linestyle='--')
ax2 = fig.add_subplot(1,2,2)
ax2.scatter(data1,data3)
plt.grid(linestyle='--')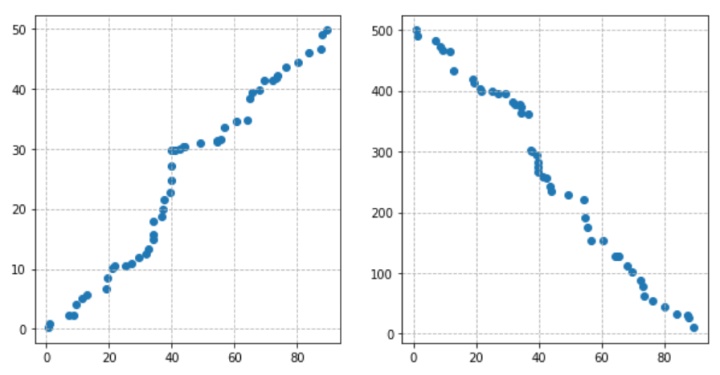
#散点矩阵
data = pd.DataFrame(np.random.randn(200,4)*100,columns=['A','B','C','D'])
pd.plotting.scatter_matrix(data,figsize=(10,6),
c = 'b',
marker = '+',
diagonal='hist',
hist_kwds={'bins':50,'edgecolor':'k'},
alpha = 0.5,
range_padding=0.1)
data.head()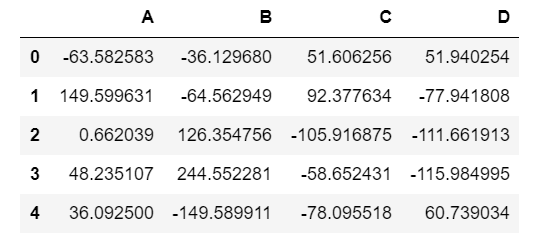

# Pearson相关系数
data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
'value2':data2.values})
print(data.head())
print('------')
# 创建样本数据
u1,u2 = data['value1'].mean(),data['value2'].mean() # 计算均值
std1,std2 = data['value1'].std(),data['value2'].std() # 计算标准差
print('value1正态性检验:n',stats.kstest(data['value1'], 'norm', (u1, std1)))
print('value2正态性检验:n',stats.kstest(data['value2'], 'norm', (u2, std2)))
print('------')
# 正态性检验 → pvalue >0.05
data['(x-u1)*(y-u2)'] = (data['value1'] - u1) * (data['value2'] - u2)
data['(x-u1)**2'] = (data['value1'] - u1)**2
data['(y-u2)**2'] = (data['value2'] - u2)**2
print(data.head())
print('------')
# 制作Pearson相关系数求值表
r = data['(x-u1)*(y-u2)'].sum() / (np.sqrt(data['(x-u1)**2'].sum() * data['(y-u2)**2'].sum()))
print('Pearson相关系数为:%.4f' % r)
# 求出r
# |r| > 0.8 → 高度线性相关value1 value2
0 0.678218 0.264657
1 0.683882 0.322216
2 1.050526 1.070748
3 1.647541 1.266555
4 4.637911 1.311668
------
value1正态性检验:
KstestResult(statistic=0.06715860692623049, pvalue=0.776789229095759)
value2正态性检验:
KstestResult(statistic=0.09553536914391403, pvalue=0.3024936582605874)
------
value1 value2 (x-u1)*(y-u2) (x-u1)**2 (y-u2)**2
0 0.678218 0.264657 1203.715631 2501.023716 579.335298
1 0.683882 0.322216 1200.701088 2500.457191 576.567800
2 1.050526 1.070748 1154.741738 2463.923902 541.180870
3 1.647541 1.266555 1131.250617 2405.011158 532.108949
4 4.637911 1.311668 1060.192849 2120.652561 530.029717
------
Pearson相关系数为:0.9949
# Pearson相关系数 - 算法
data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
'value2':data2.values})
print(data.head())
print('------')
# 创建样本数据
data.corr()
# pandas相关性方法:data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson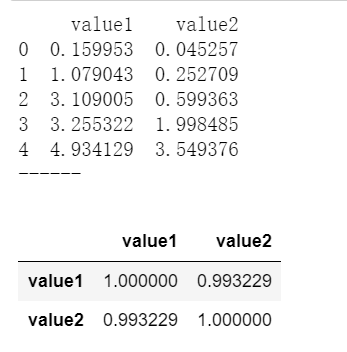
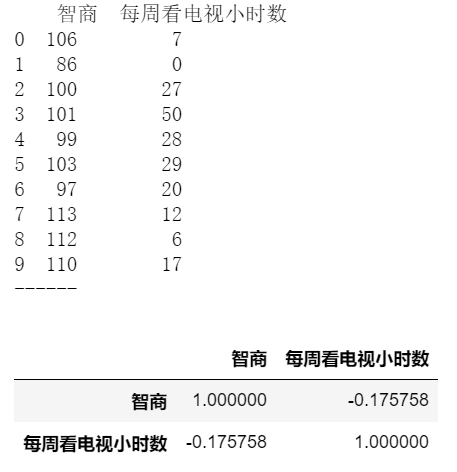
# Sperman秩相关系数
data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
'每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据
data.sort_values('智商', inplace=True)
data['range1'] = np.arange(1,len(data)+1)
data.sort_values('每周看电视小时数', inplace=True)
data['range2'] = np.arange(1,len(data)+1)
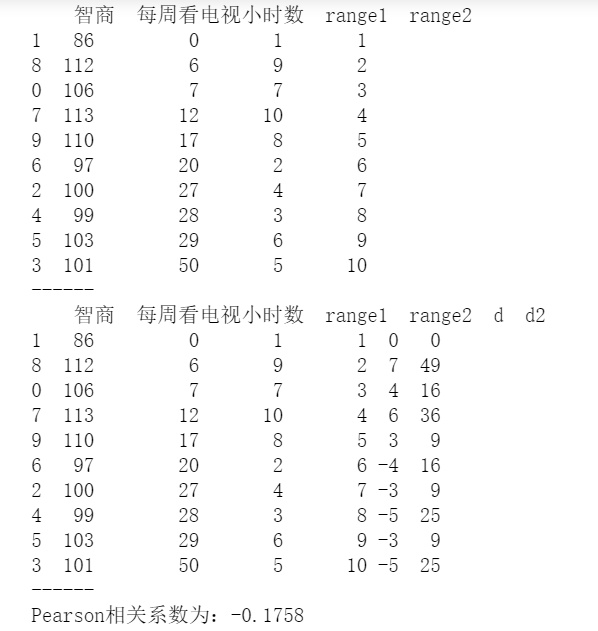
print(data)
print('------')
# “智商”、“每周看电视小时数”重新按照从小到大排序,并设定秩次index
data['d'] = data['range1'] - data['range2']
data['d2'] = data['d']**2
print(data)
print('------')
# 求出di,di2
n = len(data)
rs = 1 - 6 * (data['d2'].sum()) / (n * (n**2 - 1))
print('Pearson相关系数为:%.4f' % rs)
# 求出rs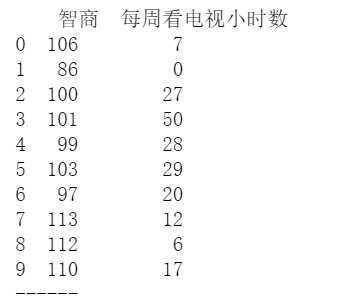
# Pearson相关系数 - 算法
data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
'每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据
data.corr(method='spearman')
# pandas相关性方法:data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson