系列文章目录

这学期选修了学习机器课程，希望记录下相关笔记和实验，小伙伴们可以跟随我的系列文章一起学习，系统深入地了解机器学习。
学习笔记：
【机器学习】第一章——机器学习分类和性能度量
【机器学习】第二章——EM（期望最大化）算法
【机器学习】第六章——概率无向图模型

实战系列：
【机器学习】实战系列一——波士顿房价预测（一文学会）
【机器学习】实战系列二——梯度下降（一文学会）
【机器学习】实战系列三——支持向量机（一文学会）
【机器学习】实战系列四——聚类实验（一文学会）
【机器学习】实战系列五——天文数据挖掘实验（天池比赛）

一、背景介绍

• 当有数据确实的时候，EM算法能够迭代地做参数估计

• 两个关键步骤：
  1. 期望步（Expectation）
  2. 最大化步（Maximization）

• 可以解决大量实际问题

二、Jessen不等式

• 推导过程可以采用归纳法证明，具体推导可以参考这个视频
• 如果f是严格的凹函数，则E[f(x)] <= f(E[x])

EM算法推导过程

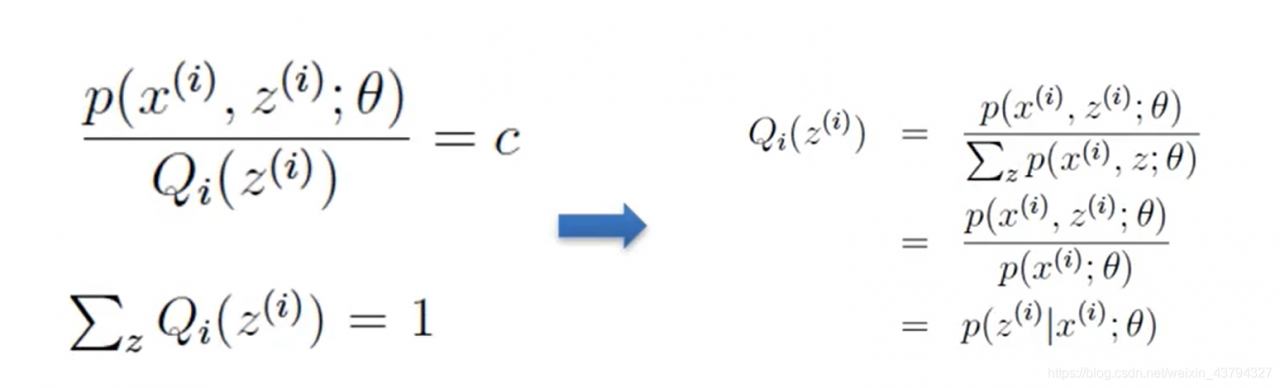
这一步推导时可以把Qi(Z(i))挪到等号右侧，再对Z(i)求和，这样容易推导出图片右侧的式子。

• E步就是求Q(i)
• M步是为了求得似然函数下界的最大值
• 如此循环直到收敛位置，我们就能求出对应的参数θ

EM函数的收敛性

如何证明EM函数是收敛的？
如果他是收敛的，那么似然的值就会逐渐增大，这就是我们要证明的内容：l(θ(t)) <= l(θ(t+1))
证明过程如下：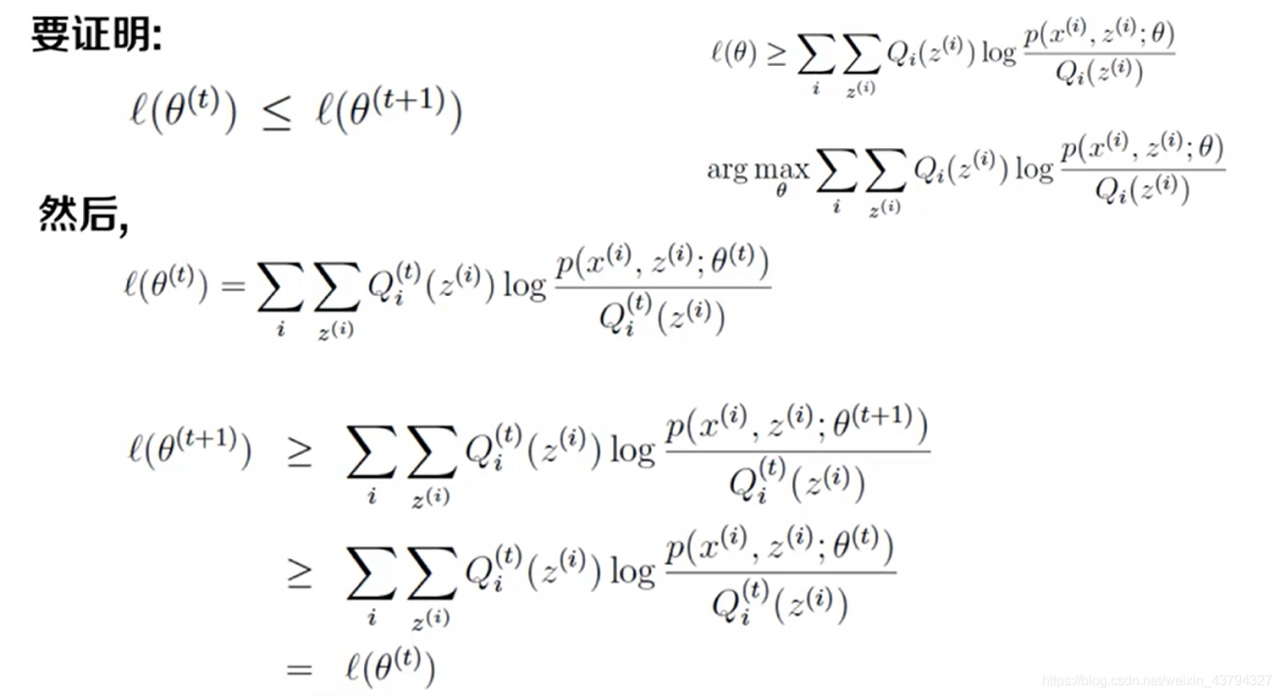

EM算法的应用

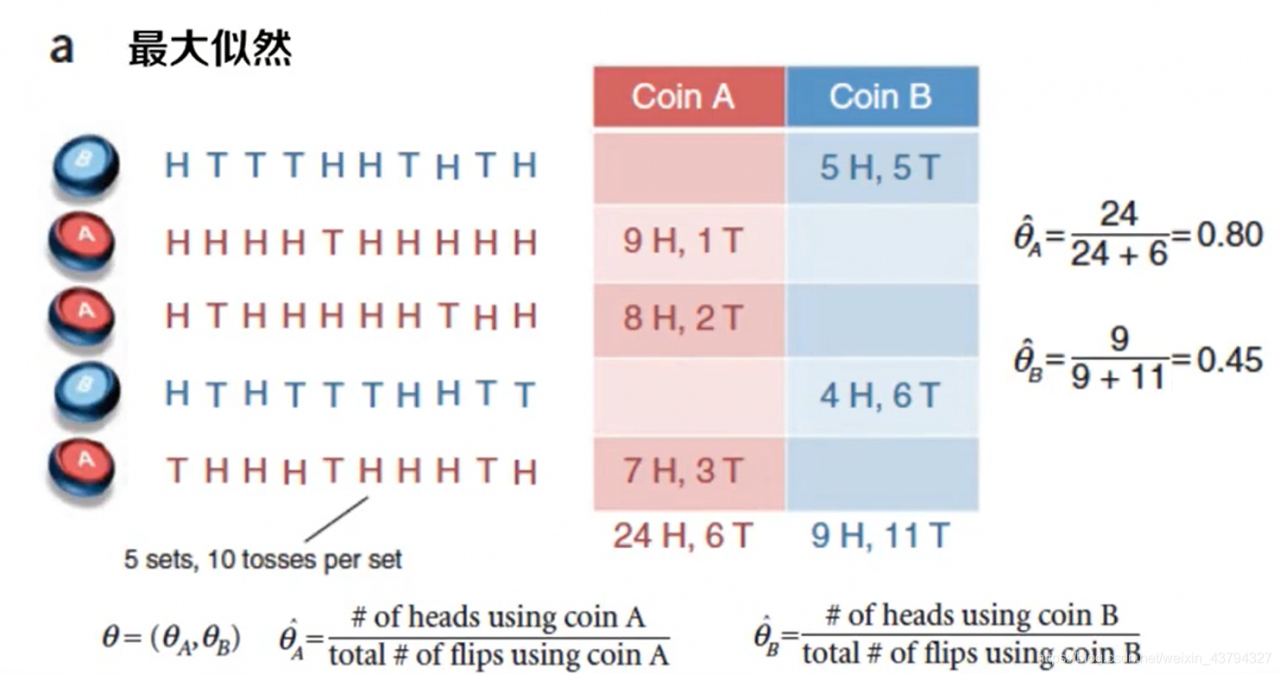
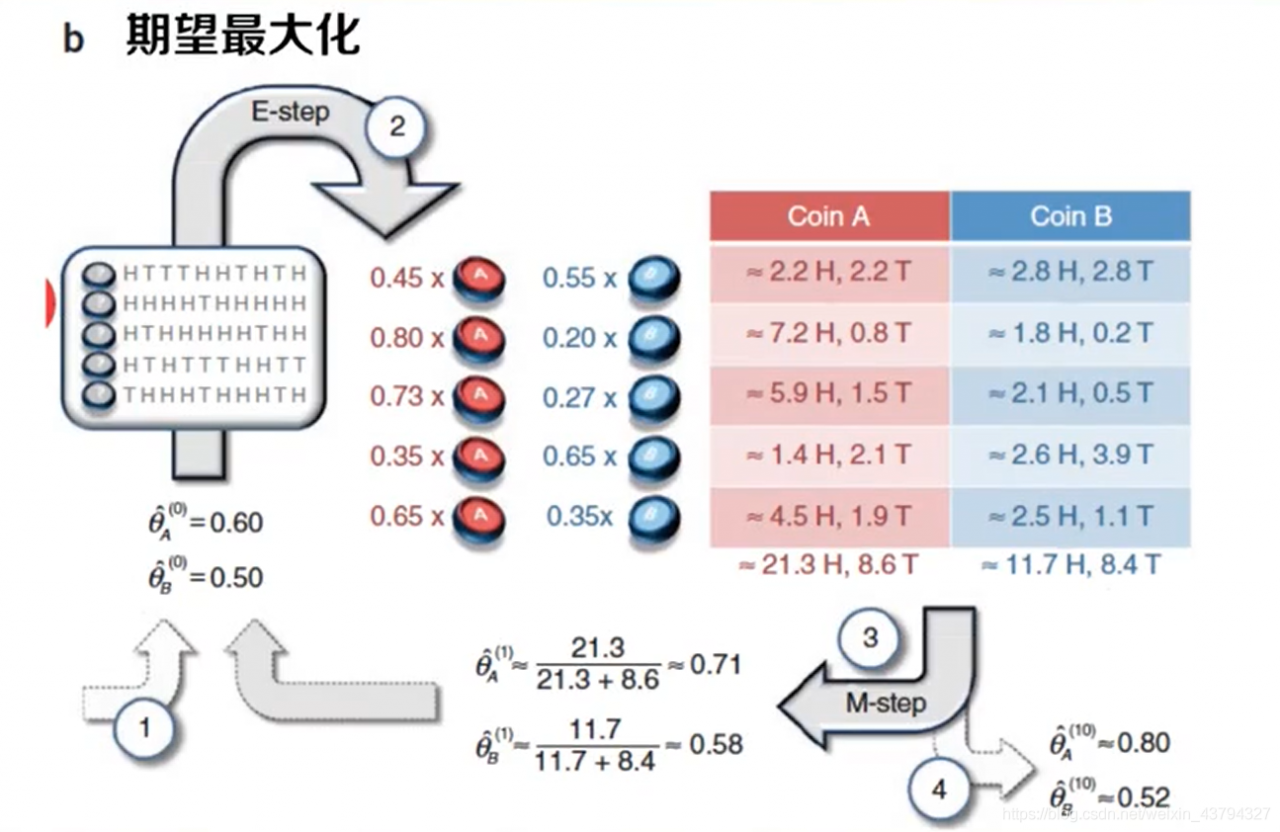
实践问题

初始化

• 数据的平均值+随机
• K-Means

终止条件

• 最大迭代次数
• 参数变化情况
• log-likelihood情况

收敛

• 局部最大，并不能找到全局最大值
• 模拟退火
• 生灭过程

数值问题

• 在协方差矩阵中引入噪音可以防止算法崩溃
• 单点可能给无穷似然

组建的数量

• 开放问题
• 采用贝叶斯方法

局限性

1. 不能够确定模型的结构
2. 不能确保找到全局最优解
3. 不能总是有很好的升级形式
4. 不能避免计算的问题（并不一定很快，或者计算量很小）

优势

1. 没有设置优化步长的问题（不像SGD要设置步长)
2. 能够直接在参数空间中工作
3. 一般训练速度很快