一. 自注意力机制

1. 自注意力机制

在深度学习中，经常使用卷积神经网络（CNN）或循环神经网络（RNN），自注意力机制对序列进行编码。使用自注意力机制将词元序列输入注意力池化中，以便同一组词元同时充当查询、键和值。具体来说每个查询都会关注所有的键－值对并生成一个注意力输出。由于查询、键和值来自同一组输入，因此被称为自注意力（self-attention）也被称为内部注意力（intra-attention） 。

2. 公式描述

给定一个由词元组成的输入序列${\mathbf{x}}_1,\dots ,{\mathbf{x}}_n$，其中任意${\mathbf{x}}_i\in {\mathbb{R}}^d$（$1\le i\le n$）。该序列的自注意力输出为一个长度相同的序列${\mathbf{y}}_1,\dots ,{\mathbf{y}}_n$，其中：

$${\mathbf{y}}_i=f({\mathbf{x}}_i,({\mathbf{x}}_1,{\mathbf{x}}_1),\dots ,({\mathbf{x}}_n,{\mathbf{x}}_n))\in {\mathbb{R}}^d$$

根据定义的注意力池化函数 ?表明自注意力机制输出张量的形状为（批量大小，时间步的数目或词元序列的长度，$d$），输出与输入的张量形状相同。

3. 比较卷积神经网络、循环神经网络和自注意力

比较下面几个架构，目标都是将由$n$个词元组成的序列映射到另一个长度相等的序列，其中的每个输入词元或输出词元都由$d$维向量表示。具体来说将比较的是卷积神经网络、循环神经网络和自注意力这几个架构的计算复杂性、顺序操作和最大路径长度。注意顺序操作会妨碍并行计算，而任意的序列位置组合之间的路径越短，则能更轻松地学习序列中的远距离依赖关系，如下图所示。

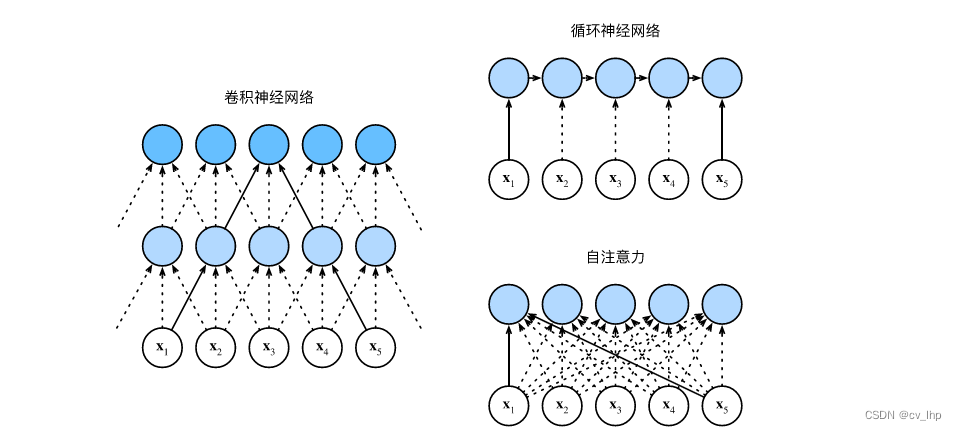
考虑一个卷积核大小为$k$的卷积层，由于序列长度是$n$，输入和输出的通道数量都是$d$，所以卷积层的计算复杂度为$\mathcal{O}(kn{d}^2)$。卷积神经网络是分层的，因此为有$\mathcal{O}(1)$个顺序操作，最大路径长度为$\mathcal{O}(n/k)$。例如${\mathbf{x}}_1$和${\mathbf{x}}_5$处于卷积核大小为3的双层卷积神经网络的感受野内。

当更新循环神经网络的隐状态时，$d\times d$权重矩阵和$d$维隐状态的乘法计算复杂度为$\mathcal{O}(d^2)$。由于序列长度为$n$，因此循环神经网络层的计算复杂度为$\mathcal{O}(n{d}^2)$。有$\mathcal{O}(n)$个顺序操作无法并行化，最大路径长度也是$\mathcal{O}(n)$。

在自注意力中，查询、键和值都是$n\times d$矩阵。考虑缩放”点－积“注意力，其中$n\times d$矩阵乘以$d\times n$矩阵。之后输出的$n\times n$矩阵乘以$n\times d$矩阵。因此，自注意力具有$\mathcal{O}(n^{2}d)$计算复杂性。每个词元都通过自注意力直接连接到任何其他词元。因此，有$\mathcal{O}(1)$个顺序操作可以并行计算，最大路径长度也是$\mathcal{O}(1)$。

因此卷积神经网络和自注意力都拥有并行计算的优势，而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方，所以在很长的序列中计算会非常慢。

4. 小结

• 在自注意力中，查询、键和值都来自同一组输入。
• 卷积神经网络和自注意力都拥有并行计算的优势，而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方，所以在很长的序列中计算会非常慢。

5. 相关链接

注意力机制第一篇：李沐动手学深度学习V2-注意力机制
注意力机制第二篇：李沐动手学深度学习V2-注意力评分函数
注意力机制第三篇：李沐动手学深度学习V2-基于注意力机制的seq2seq
注意力机制第四篇：李沐动手学深度学习V2-自注意力机制之位置编码
注意力机制第五篇：李沐动手学深度学习V2-自注意力机制
注意力机制第六篇：李沐动手学深度学习V2-多头注意力机制和代码实现
注意力机制第七篇：李沐动手学深度学习V2-transformer和代码实现