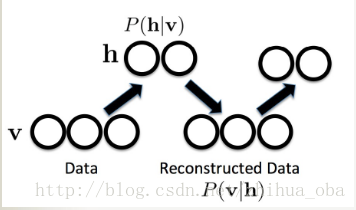
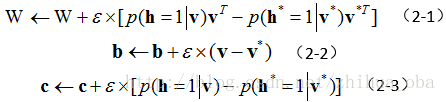受限玻尔兹曼机(RBM)+对比散度算法(CD-k) 主要内容: 受限玻尔兹曼机(RBM)基本原理 受限玻尔兹曼机(RBM)训练过程——对比散度算法(CD-k) 1. 受限玻尔兹曼机(RBM)基本原理 v h v h
受限玻尔兹曼机是一种基于能量的模型,可视层神经元向量
v 和隐藏层神经元向量
h 联合配置的能量函数为:
( 1 − 1 ) 其中,
b 为可视层偏置向量,
c 为隐藏层偏置向量,
W 为连接可视层神经元与隐藏层神经元的权重矩阵。
联合似然为:
( 1 − 2 )
条件似然函数为:
( 1 − 3 )
隐藏层各神经元的条件概率为:
( 1 − 4 )
可视层各神经元的条件概率为:
( 1 − 5 ) s i g m o i d
若 b c W x i = ( x i , 1 , x i , 2 , . . . , x i , n ) x i , j v j x i x ′ i b c W
2. 受限玻尔兹曼机(RBM)训练过程——对比散度算法(CD-k)
v v ∗ v ∗ h ∗ ε W b c v h v ∗ v v ∗ h v v v ∗
对于初学者来讲,在训练RBM的过程中,并不了解如何根据样本点 x i = ( x i , 1 , x i , 2 , . . . , x i , n ) v S ( x 1 , x 2 , . . . , x N ) j m a x i ∈ N ( x i , j ) m i n i ∈ N ( x i , j ) x i , j − m i n i ∈ N ( x i , j ) m a x i ∈ N ( x i , j ) − m i n i ∈ N ( x i , j ) δ j , 1 δ j , 2 δ j , 1 δ j , 2 δ j , 1 δ j , 2
参考文献 : 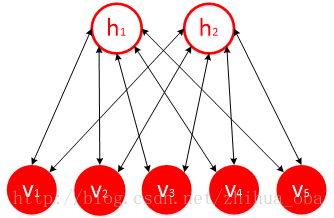
 (1−1)
(1−1)