决策树原理与代码

本文整理自《统计学习方法》第二版

1. 决策树模型与学习

定义5.1（决策树）：分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型：内部结点和叶结点，内部结点表示一个特征或属性，叶结点表示一个类。
用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点：这时，每个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分到叶结点的类中。
决策树与条件概率分布：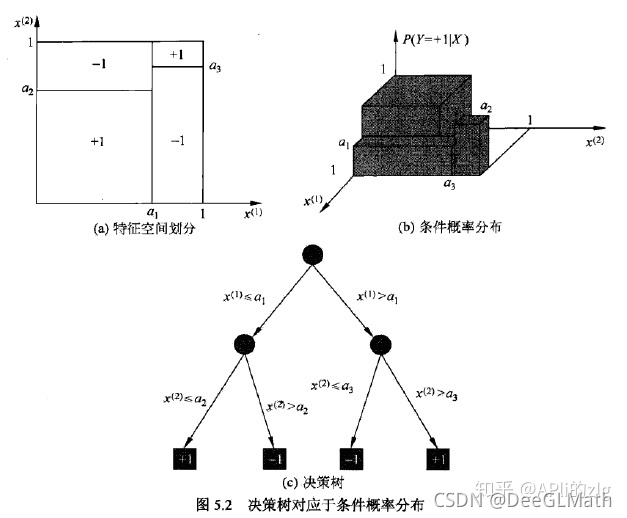

决策树学习：
假设给定训练数据集：
$$D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\text{\hspace{1em}(1)}$$
其中，$x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)}{)}^T$为输入实例（特征向量），$n$为特征个数，$y_i\in \{1,2,...,K\}$为类标记，$i=1,2,...,N$，$N$为样本容量。决策树学习的目标是根据给定的训练数据集构建一个决策树模型，使它能够对实例进行正确的分类。

决策树的本质上是从训练样本数据集中归纳出一组分类规则。与训练数据集不相矛盾的决策树（即能对训练数据进行正确分类的决策树）可能有很多个，也可能一个都没有。我们需要的是一个与训练数据矛盾较小的决策树，同时具有很好的泛化能力。我们选择的条件概率模型应该不仅对训练数据由很好的拟合，而且对未知数据有很好的预测。

2. 特征选择

特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果没有很大差别，则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。
通常，特征选择的准则是信息增益或信息增益比。
给出一个示例：（贷款申请训练数据表）

+----+--------+-----------+-------------+--------------+----------+
| ID | Age    | job_state | house_state | credit_state | category |
+----+--------+-----------+-------------+--------------+----------+
|  1 | 青年   | 否        | 否          | 一般         | 否       |
|  2 | 青年   | 否        | 否          | 好           | 否       |
|  3 | 青年   | 是        | 否          | 好           | 是       |
|  4 | 青年   | 是        | 是          | 一般         | 是       |
|  5 | 青年   | 否        | 否          | 一般         | 否       |
|  6 | 中年   | 否        | 否          | 一般         | 否       |
|  7 | 中年   | 否        | 否          | 好           | 否       |
|  8 | 中年   | 是        | 是          | 好           | 是       |
|  9 | 中年   | 否        | 是          | 非常好       | 是       |
| 10 | 中年   | 否        | 是          | 非常好       | 是       |
| 11 | 老年   | 否        | 是          | 非常好       | 是       |
| 12 | 老年   | 否        | 是          | 好           | 是       |
| 13 | 老年   | 是        | 否          | 好           | 是       |
| 14 | 老年   | 是        | 否          | 非常好       | 是       |
| 15 | 老年   | 否        | 否          | 一般         | 否       |
+----+--------+-----------+-------------+--------------+----------+

表的创建及插入数据

希望通过所给的训练数据学习一个贷款申请的决策树，用以对未来的贷款申请进行分类，即当新的客户提出贷款申请时，根据申请人的特征利用决策树决定是否批准贷款申请。

2.1 信息增益

熵的含义：表示随机变量不确定性的度量。
设$X$是一个取有限个值得离散随机变量，其概率分布为：
$$P(X=x_i)=p_i,i=1,2,...,n\text{\hspace{1em}(2)}$$
则随机变量$X$的熵定义为：
$$H(X)=-\sum _{i=1}^n{p}_i\log (p_i)\text{\hspace{1em}(3)}$$
对于上式，有如下特殊的规定：
若$p_i=0$，则定义$0\log 0=0$。通常情况下，式$(3)$中的对数以2为底数或以$e$为底（自然对数），这时熵的单位分别为比特（bit）或纳特（nat）。由定义知，熵只依赖于$X$的分布，而与$X$的取值无关，所以也可将$X$的熵记作$H(p)$，即：
$$H(p)=-\sum _{i=1}^n{p}_i\log (p_i)\text{\hspace{1em}(4)}$$
熵越大，随机变量的不确定性就越大。从定义可验证：
$$0\le H(p)\le \log (n)\text{\hspace{1em}(5)}$$
设有随机变量$(X,Y)$，其联合概率分布为：
$$P(X=x_i,Y=y_j)=p_{ij},i=1,2,...,n;j=1,2,...,m\text{\hspace{1em}(6)}$$
条件熵$H(Y|X)$表示在已知随机变量$X$的条件下随机变量$Y$的不确定性。随机变量$X$给定的条件下随机变量$Y$的条件熵$H(Y|X)$，定义为$X$给定条件下$Y$的条件概率分布的熵对$X$的数学期望：
$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)\text{\hspace{1em}(7)}$$
这里，$p_i=P(X=x_i),i=1,2,...,n$。

（信息增益）特征$A$对训练数据集$D$的信息增益$g(D,A)$，定义为集合$D$的经验熵$H(D)$与特征$A$给定条件下$D$的经验条件熵$H(D|A)$之差，即：
$$g(D,A)=H(D)-H(D|A)\text{\hspace{1em}(8)}$$
差值越大，代表选择该特征值更好

设训练数据集为$D$，$|D|$表示其样本容量，即样本个数。设有$K$个类$C_k$，$k=1,2,...,K$，$|C_k|$表示属于类$C_k$的样本个数，${\sum }_{i=1}^K|C_k|=|D|$。设特征$A$有$n$个不同的取值$\{a_1,a_2,...,a_n\}$，根据特征$A$的取值将$D$划分为$n$个子集$D_1,D_2,...,D_n$，$|D_i|$为$D_i$的样本个数，${\sum }_{i=1}^n|D_i|=|D|$。记子集$D_i$中属于类$C_k$的样本的集合为$D_{ik}$，即$D_{ik}=D_i\cap C_k$，$|D_{ik}|$为$D_{ik}$的样本个数。信息增益的算法如下：

输入：训练数据集$D$和特征$A$；
输出：特征$A$对训练数据集$D$的信息增益$g(D,A)$。

1. 计算数据集$D$的经验熵$H(D)$：
   $$H(D)=-\sum _{i=1}^n\frac{|C_k|}{|D|}{\log }_2\frac{|C_k|}{|D|}\text{\hspace{1em}(9)}$$
2. 计算特征$A$对数据集$D$的经验条件熵$H(D|A)$：
   $$H(D|A)=\sum _{i=1}^n\frac{|D_i|}{|D|}H(D_i)=-\sum _{i=1}^n\frac{|D_i|}{|D|}\sum _{i=1}^K\frac{|D_{ik}|}{|D_i|}{\log }_2\frac{|D_{ik}|}{|D_i|}\text{\hspace{1em}(10)}$$
3. 计算信息增益：
   $$g(D,A)=H(D)-H(D|A)\text{\hspace{1em}(11)}$$

2.2 信息增益比

特征$A$对训练数据集$D$的信息增益比$g_R(D,A)$定义为其信息增益$g(D,A)$与训练数据集$D$关于特征$A$的值的熵$H_A(D)$之比，即：
$$g_R(D,A)=\frac{g(D,A)}{H_A(D)}\text{\hspace{1em}(12)}$$
其中，$H_A(D)=-{\sum }_{i=1}^n\frac{|D_i|}{|D|}{\log }_2\frac{|D_i|}{|D|}$，$n$是特征$A$取值的个数。
代码：（采用贷款申请训练数据表）

# 定义信息熵函数
def empirical_entropy(data):
    p_i = pd.value_counts(data) / len(data)
    return sum(np.log2(p_i) * p_i * (-1))

# 定义条件熵函数
def empirical_conditional_entropy(data,strA,strD):
    a = data.groupby(strA).apply(lambda x: empirical_entropy(x[strD]))
    b = pd.value_counts(data[strA]) / len(data[strD])
    c = sum(a*b)
    return c

# 定义信息增益函数
def information_gain(data,strA,strD):
    return empirical_entropy(data[strD]) - empirical_conditional_entropy(data,strA,strD)

# 定义信息增益比函数
def information_gain_ratio(data,strA,strD):
    return information_gain(data,strA,strD) / empirical_entropy(data[strA])

# 选择最优特征
K = 'category'
Ai = list(df.columns[1:5])
for i in Ai:
    print('g(D,',i,'): ',information_gain(df,i,K)) # 偏向于选择取值较多的特征的问题
    # print('gR(D,',i,'): ',information_gain_ratio(df,i,K))

3. ID3、C4.5与CART算法

ID3、C4.5与CART算法 详细理论推导