Key Concepts on Deep Neural Networks

1. What is the “cache” used for in our implementation of forward propagation and backward propagation?

• We use it to pass $Z$ computed during forward propagation to the corresponding backward propagation step. It contains useful values for backward propagation to compute derivatives.
• It is used to cache the intermediate values of the cost function during training.
• It is used to keep track of the hyperparameters that we are searching over, to speed up computation.
• We use it to pass variables computed during backward propagation to the corresponding forward propagation step. It contains useful values for forward propagation to compute activations.

2. Which of the following are “parameters” of a neural network? (Check all that apply.)

• $L$ the number of layers of the neural network.
• $W^{[l]}$ the weight matrices.
• $g^{[l]}$ the activation functions.
• $b^{[l]}$ the bias vector.
  （注意，W和b为参数，L和g为超参数，二者为不同的概念）

3. Which of the following is more likely related to the early layers of a deep neural network?(只提供正确答案)
   
4. Vectorization allows you to compute forward propagation in an L-layer neural network without an explicit for-loop (or any other explicit iterative loop) over the layers l=1, 2, …,L. True/False?

• False
• True

5. Assume we store the values for $n^{[l]}$ in an array called layer_dims, as follows: layer_dims = [$n_x$, 4,3,2,1]. So layer 1 has four hidden units, layer 2 has 3 hidden units and so on. Which of the following for-loops will allow you to initialize the parameters for the model?(只提供正确答案)

• for i in range(1, len(layer_dims)):
  parameter[‘W’ + str(i)] = np.random.randn(layer_dims[i], layer_dims[i-1]) * 0.01
  parameter[‘b’ + str(i)] = np.random.randn(layer_dims[i], 1) * 0.01

6. Consider the following neural network:
   
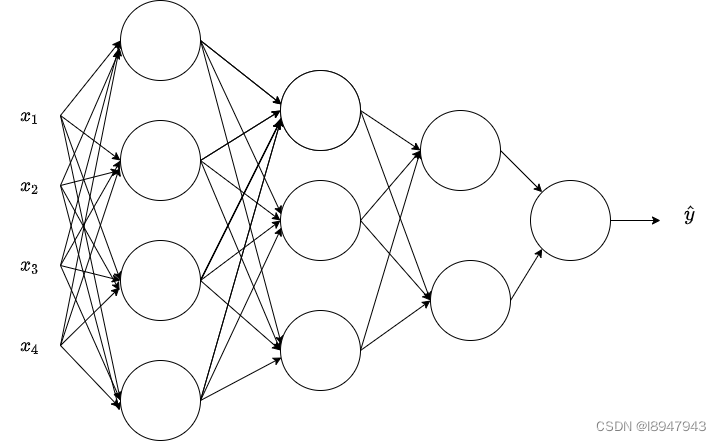
   What are all the values of $n^{[0]}$, $n^{[1]}$, $n^{[2]}$, $n^{[3]}$ and $n^{[4]}$?

• 4, 4, 3, 2, 1
• 4, 3, 2, 1
• 4, 4, 3, 2
• 4, 3, 2

7. During forward propagation, in the forward function for a layer $l$ you need to know what is the activation function in a layer (sigmoid, tanh, ReLU, etc.). During backpropagation, the corresponding backward function also needs to know what is the activation function for layer $l$, since the gradient depends on it. True/False?

• False
• True

8. For any mathematical function you can compute with an L-layered deep neural network with N hidden units there is a shallow neural network that requires only $\log N$ units, but it is very difficult to train.

• False
• True
  (原因：On the contrary, some mathematical functions can be computed using an L-layered neural network and a given number of hidden units; but using a shallow neural network the number of necessary hidden units grows exponentially.)

9. Consider the following 2 hidden layers neural network:
   
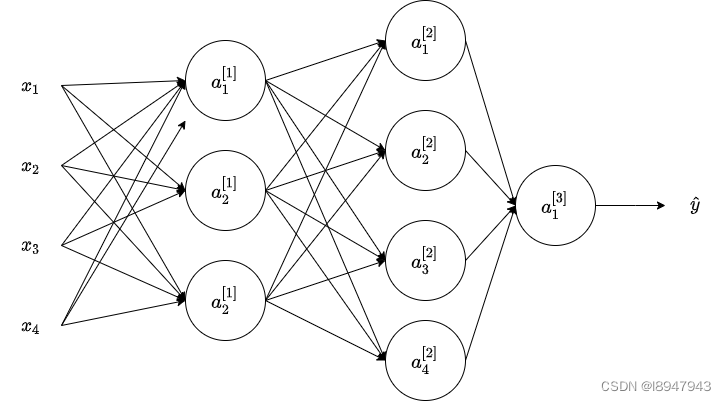
   Which of the following statements are true? (Check all that apply).

• $W^{[2]}$ will have shape (3, 1)
• $W^{[2]}$ will have shape (4, 3)
• $W^{[1]}$ will have shape (3, 4)
• $W^{[2]}$ will have shape (3, 4)
• $b^{[1]}$ will have shape (1, 3)
• $W^{[1]}$ will have shape (4, 3)
• $b^{[1]}$ will have shape (4, 1)
• $b^{[1]}$ will have shape (3, 1)
• $W^{[2]}$ will have shape (1, 3)

10. Whereas the previous question used a specific network, in the general case what is the dimension of $b^{[l]}$, the bias vector associated with layer l?

• $b^{[l]}$ has shape (1,$n^{[l-1]}$)
• $b^{[l]}$ has shape ($n^{[l-1]}$,1)
• $b^{[l]}$ has shape ($n^{[l]}$,1)
• $b^{[l]}$ has shape (1,$n^{[l]}$)