计算机视觉——全景拼接

一：图像拼接

1.1原理解析

将SIFT应用到图像拼接上，根据特征点匹配的方式，则利用这些匹配的点来估算单应矩阵使用RANSAC算法，也就是把其中一张通过个关联性和另一张匹配的方法。通过单应性矩阵H，可以将原图像中任意像素点坐标转换为新坐标点，转换后的图像即为适合拼接的结果图像。

1.2图像拼接基本流程

1.针对某个场景拍摄多张/序列图像

2.计算第二张图像与第一张图像之间的变换关系

3.将第二张图像叠加到第一张图像的坐标系中

4.变换后的融合/合成

5.在多图场景中，重复上述过程

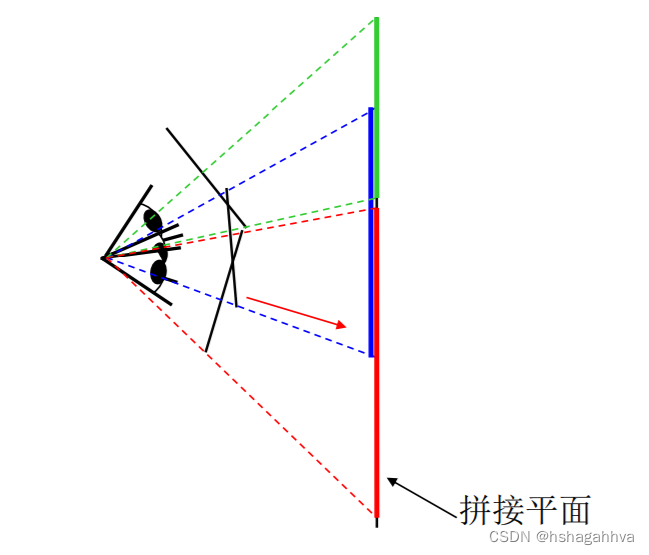
1.3RANSAC算法

随机抽样一致算法,采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数。RANSAC算法假设数据中包含正确数据和异常数据（或称为噪声。正确数据记为内点（inliers），异常数据记为外点（outliers）。同时RANSAC也假设，给定一组正确的数据，存在可以计算出符合这些数据的模型参数的方法。

RANSAC的基本流程

1.随机选择四对匹配特征

2. 根据直接线性变换解法DLT计算单应矩阵 H ( 唯一解)

3. 对所有匹配点，计算映射误差ε= ||pi ’, H pi ||

4. 根据误差阈值，确定inliers

5. 针对最大inliers集合，重新计算单应矩阵 H

通过上述流程，每次都会有正确的点和错误的点，将正确的点代入就有下图的结果

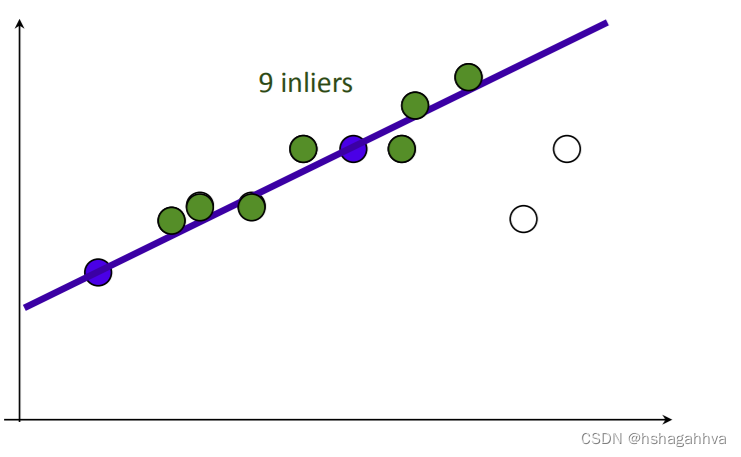
1.4单应性矩阵

单应性矩阵与射影矩阵基本是一回事，都有8个自由度，摄影矩阵是从二维平面的操作。单应性矩阵可以看成从二维的操作到三维操作的一个过度。单应性矩阵(H)可以描述两个图片之间的变换，可以进行图片的拼接

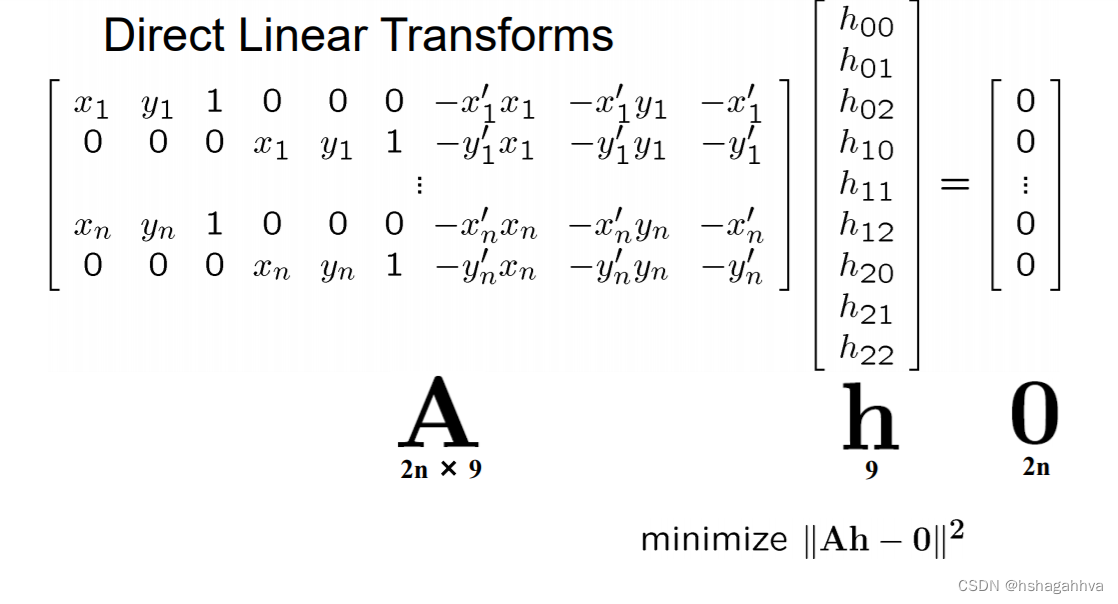
这里H是单应性矩阵，可以从一个图像把每一个变换像素到另一个图像平面，这样就可以进行图像的拼接。利用单应性矩阵做图像拼接的时候，如果之灾二维的空间中处理，要求相机的中心不能有平移，因为这样可以在不知道场景深度信息的条件下就可以完成图像的拼接。如果相机中心有移动就可能产生重影，因为这个时候两个相机看到的场景可能会不一致。

在数学几何的层面来看，利用单应性矩阵做图像拼接是要求相机中心点不能移动，但拍室外的话，因为场景较远，相机移动的距离相比于场景的距离可以忽略不记，所以拍出来的效果还好。拍室内的话，因为场景较近，要是有移动，会有很多重影。

二：实验测试

# coding=gbk
#-*- codeing =utf-8 -*-


from pylab import *
from numpy import *
from PIL import Image

# If you have PCV installed, these imports should work

from PCV.geometry import homography, warp
from PCV.localdescriptors import sift
np.seterr(invalid='ignore')
"""
This is the panorama example from section 3.3.
"""

# 设置数据文件夹的路径
featname = ['D:/SVMCV/data/image/1.jpg']
imname = ['D:/SVMCV/data/image/2.jpg']

# 提取特征并匹配使用sift算法
l = {}
d = {}
for i in range(5):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(4):
    matches[i] = sift.match(d[i + 1], d[i])

# 可视化匹配
for i in range(4):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i + 1]))
    figure()
    sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)


# 将匹配转换成齐次坐标点的函数
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j + 1][ndx, :2].T)
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2, :2].T)

    # switch x and y - TODO this should move elsewhere
    fp = vstack([fp[1], fp[0], fp[2]])
    tp = vstack([tp[1], tp[0], tp[2]])
    return fp, tp


# 估计单应性矩阵
model = homography.RansacModel()

fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0]  # im 1 to 2

fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0]  # im 0 to 1

tp, fp = convert_points(2)  # NB: reverse order
H_32 = homography.H_from_ransac(fp, tp, model)[0]  # im 3 to 2

tp, fp = convert_points(3)  # NB: reverse order
H_43 = homography.H_from_ransac(fp, tp, model)[0]  # im 4 to 3

# 扭曲图像
delta = 2000  # for padding and translation用于填充和平移

im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12, im1, im2, delta, delta)

im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12, H_01), im1, im_12, delta, delta)

im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32, im1, im_02, delta, delta)

im1 = array(Image.open(imname[4]), "f")
im_42 = warp.panorama(dot(H_32, H_43), im1, im_32, delta, 2 * delta)

figure()
imshow(array(im_42, "uint8"))
axis('off')
show()

结果展示：

原文链接：https://blog.csdn.net/hshagahhva/article/details/125354844