Python可以方便地计算数学序列和序列。在
我们找到计算到n的所有值的和
给定
以下数学组成部分:
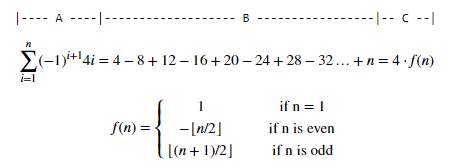
现在我们实现了两种方法A和{},由B验证。在
编码import itertools as it
n = 8
生成函数,A
^{pr2}$
求和方程,Cdef f(n):
if n == 1:
return 1
elif n % 2 == 0:
return -n // 2
else:
return (n + 1) // 2
4*f(n)
# -16
详细信息
生成函数
第一种方法只是对列表理解生成的算术序列求和。值的符号由表达式(-1)**(i + 1)交替:seq
# [4, -8, 12, -16, 20, -24, 28, -32]
类似地,可以使用生成器表达式和^{}生成无限序列:inf_seq = ((-1)**(i + 1)*(4 * i) for i in it.count(1))
sum(it.islice(inf_seq, n))
# -16
这里返回n值片段的和。注意,我们可以使用^{} itertools recipe和^{}来计算任意数量的总和,例如10和(另请参见^{})。在def take(n, iterable):
"Return first n items of the iterable as a list"
return list(it.islice(iterable, n))
inf_seq = ((-1)**(i + 1)*(4 * i) for i in it.count(1))
list(take(10, it.accumulate(inf_seq)))
# [4, -4, 8, -8, 12, -12, 16, -16, 20, -20]
求和方程
第二种方法来自检查,其中模式是根据样本序列的输出确定的:n 4n f(n) 4f(n)
--- ---- ---- -----
1 4 1 -> 4
2 -8 -1 -> -4
3 12 2 -> 8
4 -16 -2 -> -8
5 20 3 -> 12
6 -24 -3 -> -12
7 28 4 -> 16
8 -32 -4 -> -16
9 36 5 -> 20
10 -40 -5 -> -20
对于任意的最终值n,将生成序列的值(4n)。当与某个未知函数f(n)相乘时,计算出一个结果和(4f(n))。我们通过推导序列值与期望和之间的关系来确定f(n)的模式。一旦确定,我们就直接实现一个计算所需和的函数。在
亮点从列表理解可以生成数学序列。在
从生成器表达式可以生成无限序列。在
数学级数/生成函数可以使用应用于序列的约化函数来计算,例如sum(),operator.mul()等。在
一般求和方程可以实现为简单的Python函数。在