1.颜色特征
1.1 量化颜色直方图
适用于RGB、HSV等颜色空间。
操作:颜色空间量化,单位(bin)由单元中心代表,即统计落在量化单元上的像素数量
最常用的方法是将颜色空间的各个分量(维度)均匀地进行划分。
1.2 聚类颜色直方图
适用Lab等颜色空间。
操作:使用聚类算法对所有像素点颜色向量进行聚类,单元(bin)由聚类中心代表。
聚类算法则考虑到图像颜色特征再整个空间地分布情况,避免出现大量地bin中地像素数量非常稀疏的情况。
问题
当两幅图像的颜色直方图几乎相同,只是互相错开了一个bin时,如果采用L1距离或欧拉距离计算二者的相似度,会得到一个很小的值。为克服这个缺陷,需要考虑到相似但不相同的颜色之间的相似度:
- 次啊用二次式距离
- 对颜色直方图事先进行平滑过滤,即每个bin中的像素对于相邻的几个bin也由贡献。
2.几何特征:边缘
边缘:像素明显变化的区域,具有丰富的语义信息,可以用于物体识别、几何或视角变换。
边缘定义(数学上):像素值函数快速变化的区域→ \to→一阶导数的极值区域。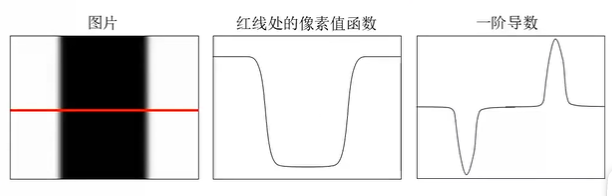
对于上图中的图3(一阶导数),边缘对应一阶导数极值。
边缘提取:先进行高斯去噪(高斯平滑),再使用一阶导数获取极值。(导数对噪声敏感)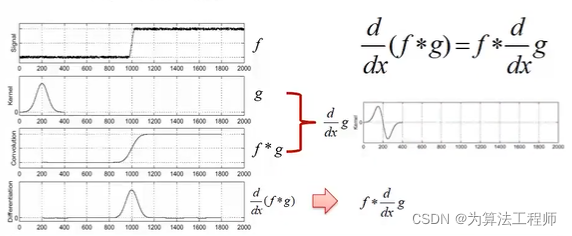
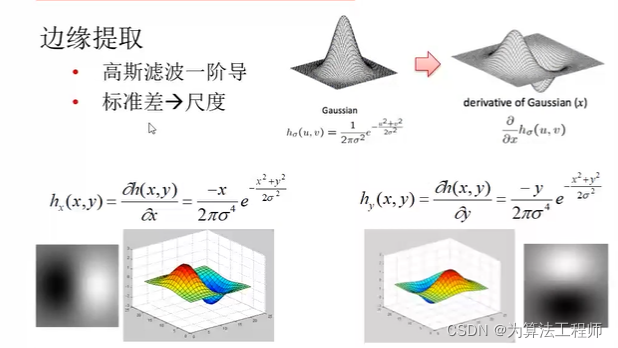
对于斜方向的图片:求两个方向的高斯滤波一阶导
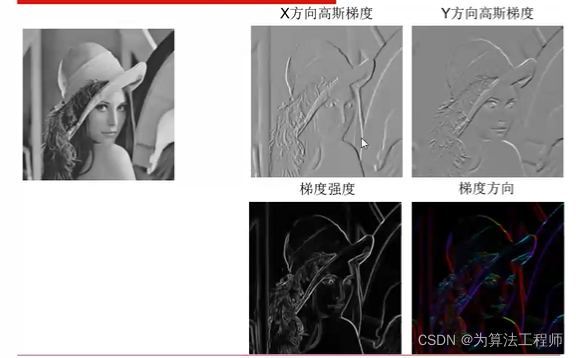
问题
边缘提取尺度问题:即不同标准差(高斯函数中的σ \sigmaσ)的滤波,不同的σ \sigmaσ可捕捉到不同尺度的边缘
3.基于特征点的特征描述子
从不同的距离,不同的方向、角度,不同的光照条件下观察一个物体时,物体的大小、形状、明暗都会有所不同。但是对于同一物体来说,即便环境条件不同,模型仍需要判断出它是同一个物体。
因此,理想的特征描述子应该具有以下性质:即在大小、方向、明暗不同的图像中,同一特征点应具有足够相似的描述子,称之为描述子的可复现性。
这些特征描述子也称之为特征点或关键点。
性质:
可用于:
最显著的特征:角点。角点检测
拉普拉斯梯度:
高斯拉普拉斯滤波:
G ( x , y , σ ) = 1 2 π σ 2 e − ( x 2 + y 2 ) / 2 σ 2 G(x, y, \sigma) = \frac{1}{2 \pi \sigma^2} e^{- (x^2 + y^2) / 2 \sigma^2}G(x,y,σ)=2πσ21e−(x2+y2)/2σ2
二阶导:
▽ 2 G = ∂ 2 ∂ x 2 G + ∂ 2 ∂ y 2 G = − 2 σ 2 + x 2 + y 2 2 π σ 6 e − ( x 2 + y 2 ) / 2 σ 2 \triangledown^2 G = \frac{\partial^2}{\partial x^2}G + \frac{\partial^2}{\partial y^2}G = \frac{- 2\sigma^2 + x^2 + y^2 }{2 \pi \sigma^6} e^{- (x^2 + y^2) / 2 \sigma^2 }▽2G=∂x2∂2G+∂y2∂2G=2πσ6−2σ2+x2+y2e−(x2+y2)/2σ2

基于尺度空间不变的特征:局部特征3.SIFT/SURF算算法