GBDT这个名字非常有深意：G-gradient（表示该算法是基于梯度的），B-Boosting（表示该算法是boosting模型），DT-decision tree（表示算法内部使用的是决策树）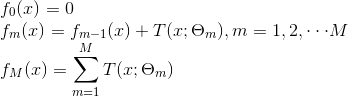

1 梯度与残差

在RF、Adaboost等加法模型中，都是通过直接拟合真实值来构建模型的，而在GBDT里面（下面这句话是重点，认真理解，并且多读几遍）：非首轮迭代的模型拟合的目标值不再是真实值，而是一个梯度值，主要是通过拟合损失函数的负梯度值在当前模型的值来构建模型。其梯度值表达式如下：

$r_{mi} = -\left [ \frac{\partial L(y_{i},f(x_{i}))}{\partial f(x_{i})}\right ]_{f(x) = f_{m-1}(x)}$

当损失函数为平方损失的时候，损失函数可以表示为：

$L(y_{i},f(x_{i})) = \frac{1}{2} (y_{i} - f(x_{i}))^{2}$

此时当前模型下损失函数的负梯度值正好等于残差： $r_{mi} = y_{i} - f(x_{i})$

2 原理剖析(回归问题)

2.1 算法流程

在2001年的论文《Greedy function approximation: A gradient boosting machine》(有时间可以仔细推敲，很不错，包括二分类/回归、多分类/回归情况)中，介绍了梯度提升的基本思想，本文仅仅摘录了论文gradient boosting思想部分（如果想要全面了解GBDT，还请读者移步到原始paper中），梯度提升的算法流程如下：

算法解析：

第1行初始化模型，估计损失函数极小化的常数值；
第2行迭代的训练M个子模型；
第3-6行为子模型的训练细节，
- 首先第3行是计算损失函数 $L(y_{i},F(x_{i}))$ 在当前模型 $F(x_{i})$ 的负梯度值，将其作为残差的估计值；
- 第4行是使用负梯度值 $\hat{y_{i}}$ 作为目标值，拟合一颗回归树模型 $h(x_{i};a)$ ，从而得到当前模型的参数 $a_{m}$
- 第5行是一个线性搜索过程，论文中将其成为Shrinkage( $\rho _{m}$ ,学习率)。
- 第6行是利用加法模型，更新回归树，得到 $F_{m}(x)$ ；

2.2 平方差loss

对于上面的算法，损失函数不一样就会产生不同变形算法，具体内容读者可以参考原paper，这里暂且举一个例子来说明一下。当损失函数为平方损失时，各个阶段的变换为：

当 $L(y_{i},F(x_{i})) = \frac{1}{2} (y_{i} - F(x_{i}))^{2}$ ，Algorithm 1中第3行的 $\hat{y_{i}} = y_{i} - F_{m-1}(x_{i})$ ，即残差（真实值-当前模型的值）。那么，第4行就相当于用一个回归树模型来拟合残差。第5行的参数 $\rho _{m}$ 即为第4行的 $\beta$ ，即 $\rho _{m} = \beta _{m}$ 。由此，便得出基于平方损失函数的gradient boosting算法模型。

2.3 叶子节点值

Algorithm 2只提及了整个算法的过程，细节如何呢？前面说到GBDT采用的是CART算法来拟合模型（损失函数在当前模型的负梯度值），既然如此，每次拟合之后每颗树叶子节点的取值是多少呢？ Algorithm 3中展示的是LAD（Least-absolute-deviation）回归的regression tree的具体原理。在LAD_TreeBoost里面，算法的第4行表示的是以 $(\hat{y_{i}},x_{i})_{1}^{N}$ 为训练样本来拟合一颗回归树模型，最终得到叶子节点区域。第5行则表示如何计算第 $m$ 轮迭代中，第 $j$ 个叶子节点的值 $\gamma _{jm}$ 。其值与损失函数有关，不同的损失函数，会致使叶子节点的值也不一样。当损失函数为MSE时， $\gamma _{jm} = ave_{x_{i} \epsilon R _{jm}} \hat{y_{i}}$ ，其中 $\hat{y_{i}}$ 为负梯度值。下图为LAD损失函数的梯度提升回归树模型算法思想。

2.4 实例解析

上面对原理进行了分析之后，大致对GBDT有了进一步的认识，为了更加形象的解释GBDT的内部执行过程，这里引用《统计学习方法》里面的数据来进行进一步分析。

假设有数据集如下：

采用GBDT进行训练，为了方便，我们采用MSE作为损失函数，并且将树的深度置为1

根据Algorithm 2，首先初始化 $F _{0}(x)$ ,可以计算出 $F _{0}(x) = 7.307$ .其次，计算出损失函数在当前模型的负梯度值: $\hat{y_{i}} = y_{i} - F_{m-1}(x_{i})$ ，结果如下：

接下来，通过构建回归树来拟合损失函数在当前模型的负梯度值 $\hat{y_{i}}$

对于决策树来说，最关键的步骤就是如何选择最优的划分标准，在回归树里面，我们采用MSE来进行评估，通过对比不同切分点两个分支的MSE加和，来选择最优的切分点（加和MSE最小的点）。根据所给的数据，可以考虑的切分点为1.5、2.5、3.5、4.5、5.5、6.5、7.5、8.5、9.5.分别计算 $y_{i} - F_{0}(x_{i})$ 的值，并计算出切分后的左右两侧加和MSE最小的切分，最后得到的是6.5，此时的MSE=0.3276.找到最佳的切分点之后，我们可以得到各个叶子节点区域，并计算出 $R _{jm}$ 和 $\gamma _{jm}$ .此时， $R _{11}$ 为x小于6.5的数据， $R _{21}$ 为x大于6.5的数据。同时，

$r_{11} = \frac{1}{6}\sum_{x_{i} \epsilon R_{11}}^{^{}}y_{i} = -1.0703$

$r_{21} = \frac{1}{4}\sum_{x_{i} \epsilon R_{21}}^{^{}}y_{i} = 1.6055$

最后，更新 $F_{1}(x_{i})$ 的值， $F_{1}(x_{i}) = F_{0}(x_{i}) + \rho _{m}\sum_{j=1}^{2} \gamma _{j1} I(x_{i} \epsilon R_{j1})$ ，其中 $\rho _{m}$ 为学习率，或称shrinkage，目的是防止预测结果发生过拟合。

至此第一轮迭代便完成，后面的迭代方式与上面一样，迭代 $m$ 次后，第 $m$ 次的 $F_{m}(x)$ 即为最终的预测结果。
$F_{m}(x) = F_{m-1}(x) + \rho _{m}h(x;a_{m})$

3 二分类问题

4 并行化

4.1 思路一

Sequential Decision Tree Building 对于顺序创建gbdt来讲每棵树以及每个节点都是依次处理的假设输入数据为 N个instances 每个instances有m个特征 + 一个目标（下降目标）

算法需要遍历这一层级的每一个node，对于每个node执行一个查找分割点的过程，该过程需要遍历每个feature来找到最佳分割点。复杂度O(N*m)且不计样本排序及线性搜索

如何实现并行？

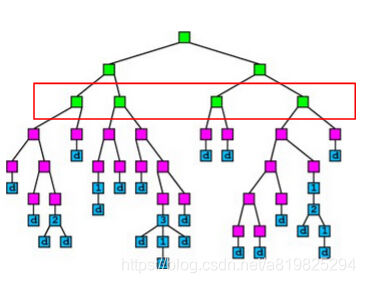
方式1：每一层的node间并行（Parallelize Node Building at Each Level）显而易见在建树过程中每一层级中的node都是相互独立的可以直接并行，但是会引起数据加载不均衡的问题workload imbalanced （决策树需要剪枝，导致一些节点是要被减掉的，如此一来会出现一些节点下的样本很多，另一些很少），比如下图红框中的四个节点第1个和第3个节点的instances数明显少于第2和第4 据说该方式效率提升不明显

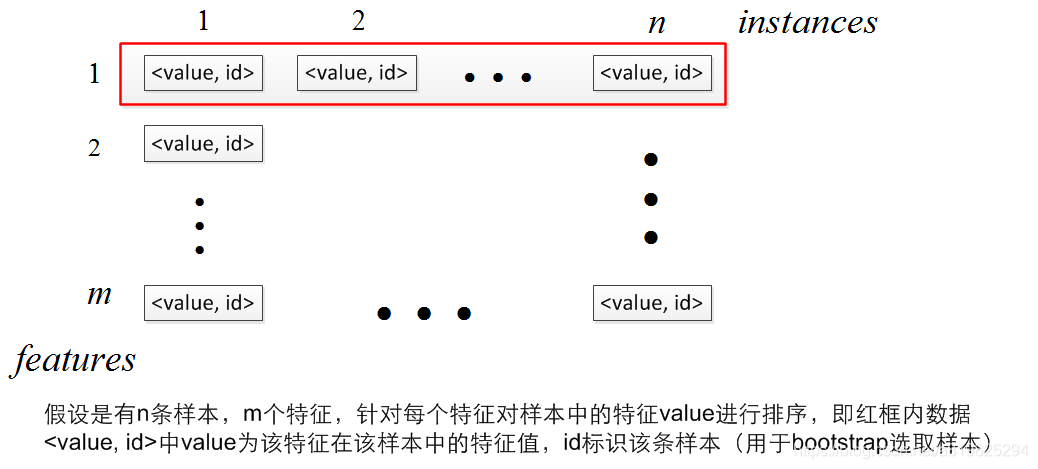
方式2：每个node上查找split分割点时候并行（node内部处理并行，Parallelize Split Finding on Each Node）也很明显，无非两个for循环的并行，方式1第一个for循环，方式2第二个for循环对于每个feature分别并行执行【将instance按照特征value排序，然后线性搜索，大家都是一个node因此instances都是一样的】，但这样也存在问题：对一些小的节点会存在过多的开销—怎么理解呢？如果一颗树建的越来越深那么分到一个node上的instances就会越来越少，我们称之为小节点，这样再对特征split过程进行并行的话。并行带来的收益可能还cover不了数据切换以及进程通信等带来的开销，如此一来随着建树越来越深并行化就体现不出其优势了。however，这是一个好的方向

方式3：在每一层对特征进行并行化(Parallelize Split Finding at Each Level by Features) 你会发现，哎呦，每一层对特征并行化，node去哪了？？？？莫急。。。在顺序建树的过程中我们发现，整个过程是通过两个循环得到的，第一个循环遍历所有叶节点，第二个遍历在每个叶节点内部遍历所有特征方式3采用颠倒两个for循环的策略，并行地去找同一层的特征分割点，只在建树开始的时候对所有特征的所有value进行排序，在遍历过程中记录对于某一特征fid其各个样本所对应的node（代码中的pos）

4.2 思路二

非递归建树
- 节点的存放

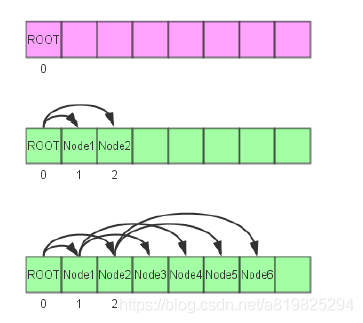
终止条件
- 树的节点数
- 树的深度
- 没有适合分割的节点
特征值排序
- 在对每个节点进行分割的时候，首先需要遍历所有的特征，然后对每个样本的特征的值进行枚举计算。（CART）
- 在对单个特征量进行枚举取值之前，我们可以先将该特征量的所有取值进行排序，然后再进行排序
- 优点
  - 避免计算重复的value值
  - 方便更佳分割值的确定
  - 减少信息的重复计算
多线程/MPI并行化的实现
- 通过MPI实现对GBDT的并行化，最主要的步骤是在建树的过程中，由于每个特征值计算最佳分割值是相互独立的，故可以对特征进行平分，再同时进行计算

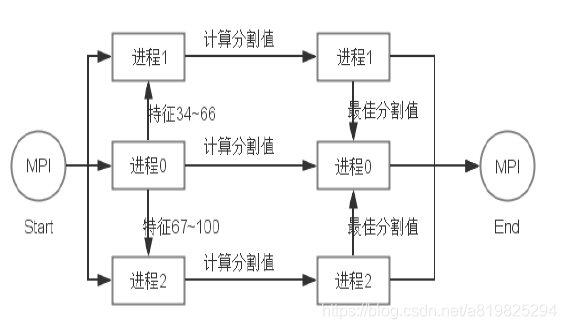
MPI并行化的实现
- 主线程

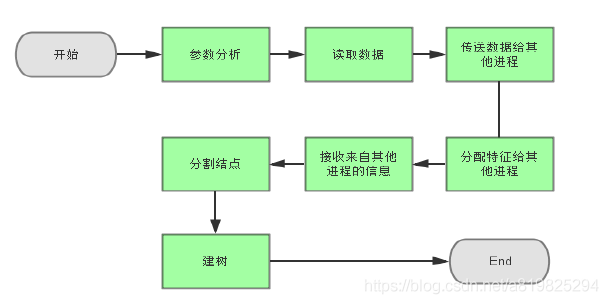
其他线程

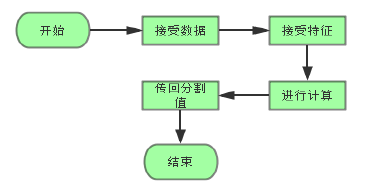# 5 参考文献 1. [Greedy function approximation: A gradient boosting machine](https://statweb.stanford.edu/~jhf/ftp/trebst.pdf) 2. 李航《统计学习方法》

原文链接：https://blog.csdn.net/a819825294/article/details/51188740