hash,hashCode,hashMap
1.前提知识
数组:
列表:

散列表
什么是hash?
hash也称散列,哈希,基本原理就是把任意长度的输入,通过Hash算法变成固定长度的输出(哈希值)。
什么是hashCode?
hashCode() 方法用于返回字符串的哈希值。就是上面说的hash算法
hash的特点:
- 1.从hash值不可以反向推导出原始的数据
- 2.输入数据的微小变化会得到完全不同的hash值,相同的数据会得到相同的值
- 3.哈希算法的执行效率要高效,长的文本也能快速地计算出哈希值
- 4.hash算法的冲突概率要小
由于hash的原理是将输入空间的值映射成hash空间内,而hash值的空间远小于输入的空间,所以一定会存在不同的输入被映射成相同输出的情况。
2.hashmap集合简介:
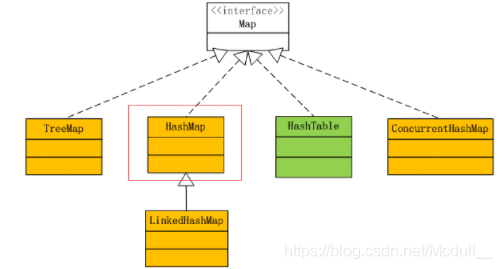
特点:
- 1.存取无序
- 2.键和值都可以是null,但键的位置只能是一个null
- 3.非线程安全
- 4.键的位置是唯一的,底层的数据结构控制键
- 5.jdk1.8以前的数据结构是 数组+链表,jdk1.8以后的是数组+链表+红黑树
- 6.阈值(边界值)>8并且数组的长度>64,才会将链表转换为红黑树,变为红黑树的目的是为了高效的查询。
Hashmap1.7之前底层结构是数组+链表。1.7之前对key,val进行put时,首先根据key来计算对应的hash值,然后根据hash值来计算出要放置的数组的索引位置,接着遍历索引所在的链表,判断当前put的结点hash值和key与链表中结点hash值key是否相等,如果相等就将新的val值替换旧的val,如果不相等,就直接addEntry()。addEntry()过程中,还要考虑扩容问题,hashmap初始容量是16,负载因子是0.75,如果一直put,就会发生resize,而在resize过程中会调用transfor()方法,转移之前的entry,转移旧的entry要进行rehash,因为1.7数据采用的是头插法,在多线程中会出现环链表,造成死循环。
map底层结构(1.8):
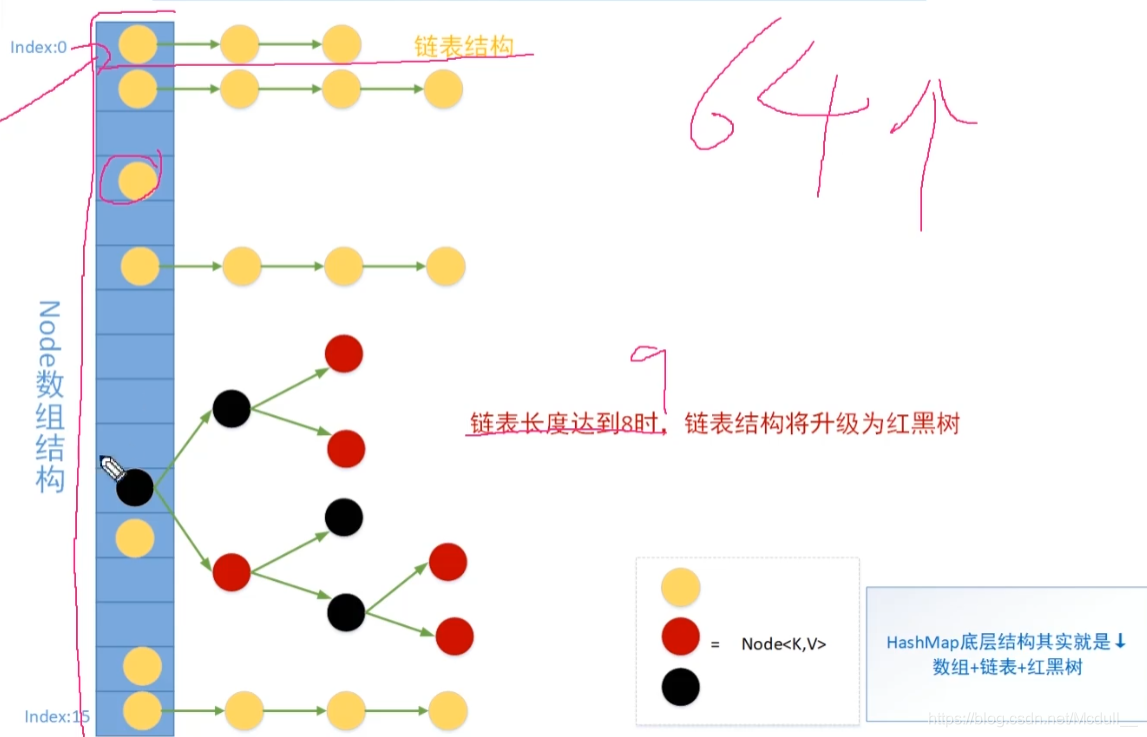
map.put过程:
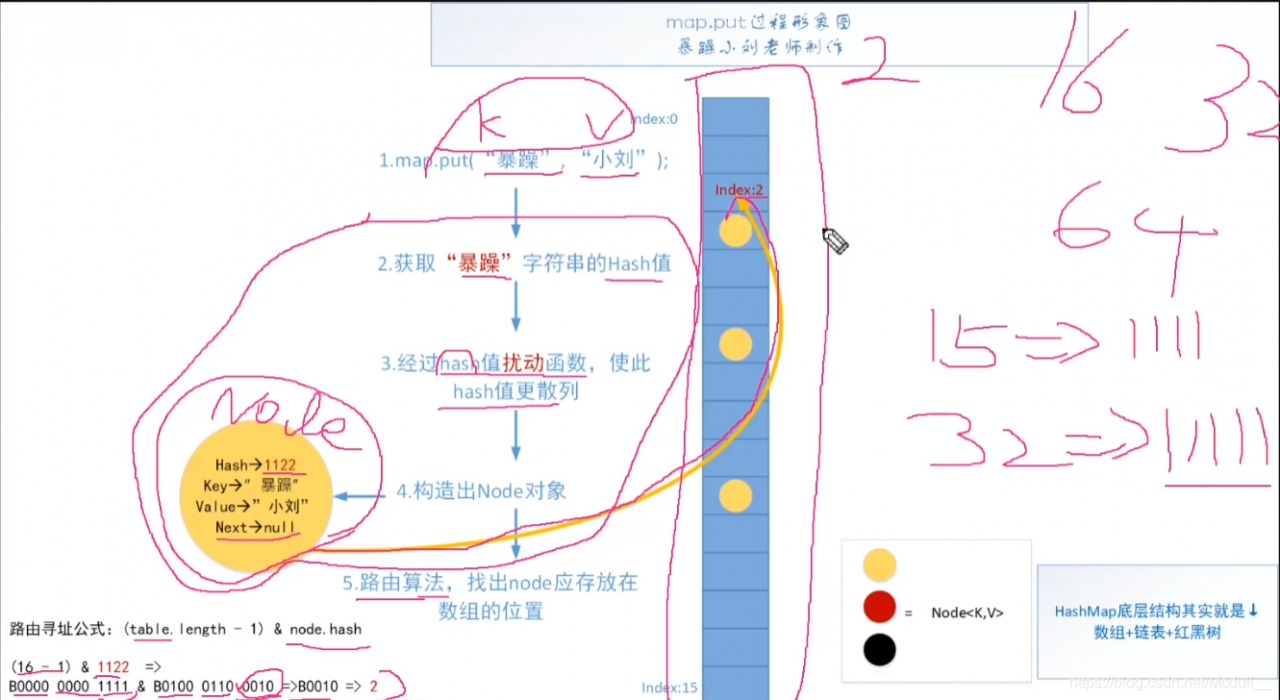
hash碰撞:当计算出来的hash值重复时或者计算出来的值转换成二进制的后四位也是“0010”(以上面例子为例),会导致路由找出来的地址重复,这样就将其放到链表中!

链化:当发生hash碰撞时,导致重复的一直加入链表中,链表的长度越来越长,导致时间复杂度越来越大。
为什么1.8引入红黑树:因为链化严重,导致时间复杂度大,所以为了查找效率高引入红黑树。
面试题:HashMap扩容机制简述:
HashMap == 数组+链表+红黑树
- HashMap默认初始桶位数是16,如果某个桶中的链表长度大于8,则先进行判断。
- 如果桶位数小于64,则先进行扩容(2倍),扩容之后重新计算哈希值,这样桶中的链表长度就变短了(之所以链表长度变短与桶的定位方式有关)
- 如果桶的位数大于64,且某个桶中的链表长度大于8,则对链表进行树化。
- 如果红黑树的节点数小于6,数也会重新变成链表。
面试题:为什么优先扩容桶位数(数组长度),而不是直接树化?
- 这样做的目的是因为,当桶位数(数组长度)比较小时,应尽量避开红黑树结构,这种情况下变为红黑树结构,反而会降低效率。因为红黑树需要逬行左旋,右旋,变色这些操作来保持平衡。同时数组长度小于64时,搜索时间相对要快些。所以结上所述为了提高性能和减少搜索时间,底层阈值大于8并且数组长度大于64时,链表才转换为红黑树,
- 而当阈值大于 8 并且数组长度大于 64 时,虽然增了红黑树作为底层数据结构,结构变得复杂了,但是,长度较长的链表转换为红黑树时,效率也变高了。
面试题:jdk1.8 中引入红黑树的进一步原因:
- jdk1.8 以前 HashMap 的实现是数组+链表,即使哈希函数取得再好,也很难达到元素百分百均匀分布。当 HashMap 中有大量的元素都存放到同一个桶中时,这个桶下有一条长长的链表,这个时候 HashMap 就相当于一个单链表,假如单链表有n个元素,遍历的时间复杂度就是O(n),完全失去了它的优势。
- 针对这种情况,jdk1.8 中引入了红黑树(查找时间复杂度为 O(logn))来优化这个问题。当链表长度很小的时候,即使遍历,速度也非常快,但是当链表长度不断变长,肯定会对查询性能有一定的影响,所以才需要转成树。
面试题: HashMap 中 hash值扰动函数是怎么实现的?还有哪些hash函数的实现方式?
- 对 key 做 hash 操作,如果key为null则直接赋哈希值为0,否则,无符号右移 16 位然后做异或位运算,如,代码所示:(key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
- 除上面的方法外,还有平方取中法,伪随机数法 和 取余数法。这三种效率都比较低,而无符号右移 16 位异或运算效率是最高的。
面试题: 当两个对象的 hashCode 相等时会怎么样?
会发生哈希碰撞。若key值内容相同则替换旧的value,不然就连接到链表后面,链表长度超过8就转换为红黑树。
如果两个键的 hashCode 相同,如何存储键值对?
通过 equals 比较内容(key)是否相同。
相同:则新的 value 覆盖之前的 value。
不相同:遍历该桶位的链表(或者树):
- 如果找到相同key,则覆盖该key对应的value;
- 如果找不到,则将新的键值对添加到链表(或者树)中;
面试题:一般用什么作为hashMap的key?
一般用Integer、String这种不可变类当HashMap的key,而且String最为常见。
1.使用Object作为Key值的时候,如Class Person (里面包含,姓名,年龄,性别,电话等属性)作为Key。当Person类中的属性改变时,导致hashCode的值也发生变化,变化后,map.get(key)因为hashCode值的变化,而无法找到之前保存的value值,同样,删除也取不到值。
解决方案是重写HashCode方法
2.避免使用Long,Integer做key。有一次项目里排查bug,最后发现这个坑,由于拆箱装箱问题,导致取不到数据。
3.hashMap源码:
基本属性与常量:
/*
* 序列化版本号
*/
private static final long serialVersionUID = 362498820763181265L;
/**
* HashMap的初始化容量(必须是 2 的 n 次幂)默认的初始容量为16
*/
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
/**
* 最大的容量为2的30次方
*/
static final int MAXIMUM_CAPACITY = 1 << 30;
/**
* 默认的装载因子
*/
static final float DEFAULT_LOAD_FACTOR = 0.75f;
/**
* 树化阈值,当一个桶中的元素个数大于等于8时进行树化
*/
static final int TREEIFY_THRESHOLD = 8;
/**
* 树降级为链表的阈值,当一个桶中的元素个数小于等于6时把树转化为链表
*/
static final int UNTREEIFY_THRESHOLD = 6;
/**
* 当桶的个数达到64的时候才进行树化
*/
static final int MIN_TREEIFY_CAPACITY = 64;
/**
* Node数组,又叫作桶(bucket)
*/
transient Node<K,V>[] table;
/**
* 作为entrySet()的缓存
*/
transient Set<Map.Entry<K,V>> entrySet;
/**
* 元素的数量
*/
transient int size;
/**
* 修改次数,用于在迭代的时候执行快速失败策略
*/
transient int modCount;
/**
* 当桶的使用数量达到多少时进行扩容,threshold = capacity * loadFactor
*/
int threshold;
/**
* 装载因子
*/
final float loadFactor;
(1)容量:容量为数组的长度,亦即桶的个数,默认为16,最大为2的30次方,当容量达到64时才可以树化。
(2)装载因子:装载因子用来计算容量达到多少时才进行扩容,默认装载因子为0.75。
(3)树化:树化,当容量达到64且链表的长度达到8时进行树化,当链表的长度小于6时反树化。
面试问题:为什么必须是 2 的 n 次幂?如果输入值不是 2 的幂比如 10 会怎么样?
HashMap 构造方法可以指定集合的初始化容量大小,如:
// 构造一个带指定初始容量和默认负载因子(0.75)的空 HashMap。 HashMap(int initialCapacity)当向 HashMap 中添加一个元素的时候,需要根据 key 的 hash 值,去确定其在数组中的具体位置。HashMap 为了存取高效,减少碰撞,就是要尽量把数据分配均匀,每个链表长度大致相同,这个实现的关键就在把数据存到哪个链表中的算法。
这个算法实际就是取余,hash % length,而计算机中直接求余效率不如位移运算。所以源码中做了优化,使用 hash & (length - 1),而实际上 hash % length 等于 hash & ( length - 1) 的前提是 length 是 2 的 n 次幂。
例如,数组长度为 8 的时候,
3 & (8 - 1) = 3,2 & (8 - 1) = 2,桶的位置是(数组索引)3和2,不同位置上,不碰撞。再来看一个数组长度(桶位数)不是2的n次幂的情况:
从上图可以看出,当数组长度为9(非2 的n次幂)的时候,不同的哈希值hash,
hash & (length - 1)所得到的数组下标相等(很容易出现哈希碰撞)。小结一下HashMap数组容量使用2的n次幂的原因:
面试问题:如果创建HashMap对象时,输入的数组长度length是10,而不是2的n次幂会怎么样呢?
HashMap<String, Integer> hashMap = new HashMap(10);
HashMap双参构造函数会通过tableSizeFor(initialCapacity)方法,得到一个最接近length且大于length的2的n次幂数(比如最接近10且大于10的2的n次幂数是16)
static final int tableSizeFor(int cap) { int n = cap - 1; n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; }举例解析一下:
-------------------------------------------------------
首先假定传入的cap = 10
则,n = 10 -1 => 9
n |= n >>> 1 就等同于 n = (n | n >>> 1),所以:
(位运算不懂的可以去看我的《Java基础提高之位运算》这篇文章)
9 => 0b1001 9 >>> 1 => 0b0100
n |= n >>> 1; ===> 0b1001 | 0b0100 => 0b1101
n |= n >>> 2; ===> 0b1101 | 0b0011 => 0b1111
n |= n >>> 4; ===> 0b1111 | 0b0000 => 0b1111
n |= n >>> 8; ===> 0b1111 | 0b0000 => 0b1111
n |= n >>> 16; ===> 0b1111 | 0b0000 => 0b1111
得到:
0b1111 => 15
返回:
return 15 + 1 => 16
-------------------------------------------------------
如果cap 不减去1,即直接使n等于cap的话,int n = cap;
我们继续用上边返回的cap => 16 传入tableSizeFor(int cap):
cap = 16
n = 16
16 => 0b10000 16 >>> 1 => 0b01000
n |= n >>> 1; ===> 0b10000 | 0b01000 => 0b11000
n |= n >>> 2; ===> 0b11000 | 0b00110 => 0b11110
n |= n >>> 4; ===> 0b11110 | 0b00001 => 0b11111
n |= n >>> 8; ===> 0b11111 | 0b00000 => 0b11111
n |= n >>> 16; ===> 0b11111 | 0b00000 => 0b11111
得到:
0b11111 => 31
返回 return 31 +1 => 32
而实际情况是应该传入cap = 16 , n = cap -1 = 15
15 => 0b1111
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
经过上面运算后得到:还是15
返回结果:
return 15 + 1 = 16
所以我们得出结果:
防止 cap 已经是 2 的幂数情况下。没有这个减 1 操作,
则执行完几条无符号位移或位运算操作之后,返回的cap(32)将是实际所需cap(16)的 2倍。
*/
当链表的值超过8则会转为红黑树(jdk1.8新增)
// 当桶(bucket)上的结点数大于这个值时会转为红黑树
static final int TREEIFY_THRESHOLD = 8;
面试问题:为什么 Map 桶中结点个数超过 8 才转为红黑树?
答:hashCode 算法下所有 桶 中结点的分布频率会遵循泊松分布,这时一个桶中链表长度超过 8 个元素的槪率非常小,权衡空间和时间复杂度,所以选择 8 这个数宇。
在 HashMap 中有一段注释说明:
Because TreeNodes are about twice the size of regular nodes, we use them only when bins contain enough nodes to warrant use (see TREEIFY_THRESHOLD). And when they become too small (due to removal or resizing) they are converted back to plain bins. In usages with well-distributed user hashCodes, tree bins are rarely used. Ideally, under random hashCodes, the frequency of nodes in bins follows a Poisson distribution (http://en.wikipedia.org/wiki/Poisson_distribution) with a parameter of about 0.5 on average for the default resizing threshold of 0.75, although with a large variance because of resizing granularity. Ignoring variance, the expected occurrences of list size k are (exp(-0.5) * pow(0.5, k) / factorial(k)). The first values are: 翻译:因为树结点的大小大约是普通结点的两倍,所以我们只在箱子包含足够的结点时才使用树结点(参见TREEIFY_THRESHOLD)。 当它们变得太小(由于删除或调整大小)时,就会被转换回普通的桶。在使用分布良好的用户 hashCode 时,很少使用树箱。 理想情况下,在随机哈希码下,箱子中结点的频率服从泊松分布。 默认调整阈值为0.75,平均参数约为0.5,尽管由于调整粒度的差异很大。忽略方差,列表大小k的预朗出现次数是(exp(-0.5)*pow(0.5, k) / factorial(k) 第一个值是: 0: 0.60653066 1: 0.30326533 2: 0.07581633 3: 0.01263606 4: 0.00157952 5: 0.00015795 6: 0.00001316 7: 0.00000094 8: 0.00000006 more: less than 1 in ten million
TreeNodes(树) 占用空间是普通 Nodes(链表) 的两倍,所以只有当 bin(bucket 桶) 包含足够多的结点时才会转成 TreeNodes,而是否足够多就是由 TREEIFY_THRESH〇LD 的值决定的。当 bin(bucket 桶) 中结点数变少时,又会转成普通的 bin(bucket 桶)。并且我们查看源码的时候发现,链表长度达到 8 就转成红黑树,当长度降到 6 就转成普通 bin(bucket 桶)。
这样就解释了为什么不是一开始就将其转换为 TreeNodes,而是需要一定结点数之后才转为 TreeNodes,说白了就是权衡空间和时间。
这段内容还说到:当 hashCode 离散性很好的时候,树型 bin 用到的概率非常小,因为数据均匀分布在每个 bin 中,几乎不会有 bin 中链表长度会达到阈值。但是在随机 hashCode 下,离散性可能会变差,然而 jdk 又不能阻止用户实现这种不好的 hash 算法,因此就可能导致不均匀的数据分布。不理想情况下随机 hashCode 算法下所有 bin 中结点的分布频率会遵循泊松分布,我们可以看到,一个 bin 中链表长度达到 8 个元素的槪率为 0.00000006,几乎是不可能事件。所以,之所以选择 8,不是随便決定的,而是裉据概率统计决定的。
table 用来初始化(必须是二的n次幂)
// 存储元素的数组
transient Node<K,V>[] table;
在 jdk1.8 中我们了解到 HashMap 是由数组加链表加红黑树来组成的结构,其中 table 就是 HashMap 中的数组,jdk8 之前数组类型是Entry<K,V> 类型。从 jdk1.8 之后是Node<K,V> 类型。只是换了个名字,都实现了一样的接口:Map.Entry<K,V>。负责存储键值对数据的。
哈希表的负载因子
// 负载因子
final float loadFactor;// 0.75f
- loadFactor 是用来衡量 HashMap 满的程度,表示HashMap的疏密程度,影响 hash 操作到同一个数组位置的概率,计算 HashMap 的实时负载因子的方法为:size/capacity。capacity 是桶的数量,也就是 table 的长度 length。
- loadFactor 太大导致查找元素效率低,太小导致数组的利用率低,存放的数据会很分散。loadFactor 的默认值为 0.75f 是官方给出的一个比较好的临界值。
- 当 HashMap 里面容纳的元素已经达到 HashMap 数组长度的 75% 时,表示 HashMap 太挤了,需要扩容,而扩容这个过程涉及到 rehash、复制数据等操作,非常消耗性能。所以开发中尽量减少扩容的次数,可以通过创建 HashMap 集合对象时指定初始容量来尽量避免。
面试题:为什么负载因子loadFactor 设置为0.75,初始化临界值threshold是12?
loadFactor 越趋近于1,那么 数组中存放的数据(entry)也就越多,也就越密,也就是会让链表的长度增加,loadFactor 越小,也就是趋近于0,数组中存放的数据(entry)也就越少,也就越稀疏。
如果希望链表尽可能少些,要提前扩容。有的数组空间有可能一直没有存储数据,负载因子尽可能小一些。
例如:负载因子是0.4。 那么16*0.4--->6 如果数组中满6个空间就扩容会造成数组利用率太低了。 负载因子是0.9。 那么16*0.9--->14 那么这样就会导致链表有点多了,导致查找元素效率低。所以既兼顾数组利用率又考虑链表不要太多,经过大量测试 0.75 是最佳方案。
threshold计算公式:capacity(数组长度默认16) * loadFactor(负载因子默认0.75)==12。
这个值是当前已占用数组长度的最大值。当Size >= threshold(12)的时候,那么就要考虑对数组的 resize(扩容),也就是说,这个的意思就是衡量数组是否需要扩增的一个标准。 扩容后的 HashMap 容量是之前容量的两倍。
hashMap构造方法:
- HashMap()
构造一个空的HashMap,默认初始容量16和默认负载因子0.75
public HashMap() {
// 将默认的负载因子0.75赋值给loadFactor,并没有创建数组
this.loadFactor = DEFAULT_LOAD_FACTOR;
}
- HashMap(int initialCapacity)
构造一个具有指定的初始容量和默认负载因子0.75的HashMap
// 指定“容量大小”的构造函数
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
- HashMap(int initialCapacity,float loadFactor)
构造一个具有指定初始容量和负载因子的HashMap
/*
指定“容量大小”和“负载因子”的构造函数
initialCapacity:指定的容量
loadFactor:指定的负载因子
*/
public HashMap(int initialCapacity, float loadFactor) {
// 判断初始化容量initialCapacity是否小于0
if (initialCapacity < 0)
// 如果小于0,则抛出非法的参数异常IllegalArgumentException
throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity);
// 判断初始化容量initialCapacity是否大于集合的最大容量MAXIMUM_CAPACITY
if (initialCapacity > MAXIMUM_CAPACITY)
// 如果超过MAXIMUM_CAPACITY,会将MAXIMUM_CAPACITY赋值给initialCapacity
initialCapacity = MAXIMUM_CAPACITY;
// 判断负载因子loadFactor是否小于等于0或者是否是一个非数值
if (loadFactor <= 0 || Float.isNaN(loadFactor))
// 如果满足上述其中之一,则抛出非法的参数异常IllegalArgumentException
throw new IllegalArgumentException("Illegal load factor: " + loadFactor);
// 将指定的负载因子赋值给HashMap成员变量的负载因子loadFactor
this.loadFactor = loadFactor;// 一般不建议修改默认的负载因子
this.threshold = tableSizeFor(initialCapacity);
}
// 最后调用了tableSizeFor,来看一下方法实现:
/*
返回比指定cap容量大的最小2的n次幂数:
举例解析一下:
-------------------------------------------------------
首先假定传入的cap = 10
则,n = 10 -1 => 9
n |= n >>> 1 就等同于 n = (n | n >>> 1),所以:
(位运算不懂的可以去看我的《Java基础提高之位运算》这篇文章)
9 => 0b1001 9 >>> 1 => 0b0100
n |= n >>> 1; ===> 0b1001 | 0b0100 => 0b1101
n |= n >>> 2; ===> 0b1101 | 0b0011 => 0b1111
n |= n >>> 4; ===> 0b1111 | 0b0000 => 0b1111
n |= n >>> 8; ===> 0b1111 | 0b0000 => 0b1111
n |= n >>> 16; ===> 0b1111 | 0b0000 => 0b1111
得到:
0b1111 => 15
返回:
return 15 + 1 => 16
-------------------------------------------------------
如果cap 不减去1,即直接使n等于cap的话,int n = cap;
我们继续用上边返回的cap => 16 传入tableSizeFor(int cap):
cap = 16
n = 16
16 => 0b10000 16 >>> 1 => 0b01000
n |= n >>> 1; ===> 0b10000 | 0b01000 => 0b11000
n |= n >>> 2; ===> 0b11000 | 0b00110 => 0b11110
n |= n >>> 4; ===> 0b11110 | 0b00001 => 0b11111
n |= n >>> 8; ===> 0b11111 | 0b00000 => 0b11111
n |= n >>> 16; ===> 0b11111 | 0b00000 => 0b11111
得到:
0b11111 => 31
返回 return 31 +1 => 32
而实际情况是应该传入cap = 16 , n = cap -1 = 15
15 => 0b1111
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
经过上面运算后得到:还是15
返回结果:
return 15 + 1 = 16
所以我们得出结果:
防止 cap 已经是 2 的幂数情况下。没有这个减 1 操作,
则执行完几条无符号位移或位运算操作之后,返回的cap(32)将是实际所需cap(16)的 2倍。
*/
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
说明:
对于this.threshold = tableSizeFor(initialCapacity);疑问?
**tableSizeFor(initialCapacity)**判断指定的初始化容量是否是2的n次幂,如果不是那么会变为比指定初始化容量大的最小的2的n次幂。
但是注意,在tableSizeFor方法体内部将计算后的数据返回给调用这里了,并且直接赋值给threshold边界值了。有些人会觉得这里是一个bug,应该这样书写:
this.threshold = tableSizeFor(initialCapacity) * this.loadFactor;
这样才符合threshold的意思(当HashMap的size到达threshold这个阈值时会扩容)
但是请注意,在jdk8以后的构造方法中,并没有对table这个成员变量进行初始化,table的初始化被推迟到了put方法中,在put方法中会对threshold重新计算。
- HashMap(Map<? extends K, ? extends V> m)
包含另一个"Map"的构造函数
// 构造一个映射关系与指定 Map 相同的新 HashMap。
public HashMap(Map<? extends K, ? extends V> m) {
// 负载因子loadFactor变为默认的负载因子0.75
this.loadFactor = DEFAULT_LOAD_FACTOR;
putMapEntries(m, false);
}
最后调用了 putMapEntries(),来看一下方法实现
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
//获取参数集合的长度
int s = m.size();
if (s > 0) {//判断参数集合的长度是否大于0
if (table == null) { // 判断table是否已经初始化
// 未初始化,s为m的实际元素个数
float ft = ((float)s / loadFactor) + 1.0F;// 得到新的扩容阈值
int t = ((ft < (float)MAXIMUM_CAPACITY) ? (int)ft : MAXIMUM_CAPACITY);// 新的扩容阈值float自动向下转型为int
// 计算得到的t大于阈值,则初始化阈值,将其变为符合要求的2的n次幂数
if (t > threshold)
threshold = tableSizeFor(t);
}
// 如果table已初始化过了,并且m元素个数大于阈值,进行扩容处理
else if (s > threshold)
resize();
// 将m中的所有元素添加至HashMap中
for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
K key = e.getKey();
V value = e.getValue();
// 得到的key 和 value 放入 hashmap
putVal(hash(key), key, value, false, evict);
}
}
}
注意:
面试问题:float ft = ((float)s / loadFactor) + 1.0F; 这一行代码中为什么要加 1.0F ?
(float)s/loadFactor 的结果是小数,加 1.0F 与 (int)ft 相当于是对小数做一个向上取整以尽可能的保证更大容量,更大的容量能够减少 resize 的调用次数(为了效率,应当尽量减少扩容的次数)。所以 + 1.0F 是为了获取更大的容量。
例如:原来集合的元素个数是 6 个,那么 6/0.75 是8,由于8是 2 的n次幂,那么
if (t > threshold) threshold = tableSizeFor(t);执行过后,新的数组大小就是 8 了。然后原来数组的数据就会存储到长度是 8 的新的数组中了,这样会导致在存储元素的时候,容量不够,还得继续扩容,那么性能降低了,而如果 +1 呢,数组长度直接变为16了,这样可以减少数组的扩容。
hashMap成员方法:
put(K key,V value)方法
put方法比较复杂,实现步骤大致如下:
- 1.通过hash值计算出key映射到哪个桶
- 2.如果桶上没有碰撞冲突,则直接插入
- 3.如果出现hash碰撞,需要处理冲突
- 如果该桶使用红黑树处理冲突,则调用红黑树的方法插入数据
- 否则采用链式方法插入,如果链的长度达到临界值,则把链表转变为红黑树
- 4.如果桶中存在重复的键,则为该键替换新值value
- 5.如果size大于阈值threshold,则进行扩容
具体的方法如下:
public V put(K key, V value) {
// 调用hash(key)计算出key的hash值
return putVal(hash(key), key, value, false, true);
}
说明:
- HashMap 只提供了 put 用于添加元素,putVal 方法只是给 put 方法调用的一个方法,并没有提供给用户使用。 所以我们重点看 putVal 方法。
- 我们可以看到在 putVal 方法中 key 在这里执行了一下 hash 方法,来看一下 hash 方法是如何实现的。
下面这里先对key求hash值,在经过扰动函数!
static final int hash(Object key) {
int h;
// 如果key为null,则hash值为0,存放在数组的最上方,只能有一个null
// 否则调用key的hashCode()方法计算出key的哈希值然后赋值给h,
// 后与h无符号右移16位后的二进制进行按位异或得到最后的hash值, (扰动函数)
// 这样做是为了使计算出的hash更分散,使高位也参与运算
// 为什么要更分散呢?因为越分散,某个桶的链表长度就越短,之后生成的红黑树越少,效率越高
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
从上面可以得知HashMap 是支持 key 为空的,而 HashTable 是直接用 Key 来获取hashCode 所以 key 为空会抛异常。
解读上述 hash 方法:
我们先研究下 key 的哈希值是如何计算出来的。key 的哈希值是通过上述方法计算出来的。
这个哈希方法首先计算出 key 的 hashCode 赋值给 h,然后与 h 无符号右移 16 位后的二进制进行按位异或得到最后的 hash 值。
在 putVal 函数中使用到了上述 hash 函数计算的哈希值:
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
...
if ((p = tab[i = (n - 1) & hash]) == null) // 这里的n表示数组长度16 ,//路由寻址公式
// (length - 1) & hash = 桶位下标 当数组长度为2的n次幂数时,
// 该公式相当于:hash % length 哈希值对数组长度取余
// 例如:hash % 32 = hash & (32-1)
...
}
回到上面:
面试题: 为什么要(h = key.hashCode()) ^ (h >>> 16)
计算过程如下所示:
说明:
- key.hashCode();返回散列值也就是 hashcode,假设随便生成的一个值。
- n 表示数组初始化的长度是 16。
- &(按位与运算):运算规则:相同的二进制数位上,都是 1 的时候,结果为 1,否则为0。
- ^(按位异或运算):运算规则:相同的二进制数位上,数字相同,结果为 0,不同为 1。
最后获得0101==> 下标为5的捅。
简单来说就是:
高16bit不变,低16bit和高16bit做了一个异或,得到32bit二进制
为什么?
如果当n,即数组长度很小,假设是16的话,那么n-1即为1111,这样的值和hashCode直接做无符号按位与操作,实际上只使用了哈希值的后4位。如果当哈希值的高位变化很大,低位变化很小,这样很容易就造成哈希冲突了,然后会导致路由找出来的地址重复,这样就将其放到链表中,又会导致查询效率变低。所以这里把高位和低位都利用起来,从而解决了这个问题。
下面,我们来看看 putVal 方法,看看它到底做了什么。
主要参数:
- hash:key 的 hash 值
- key:原始 key
- value:要存放的值
- onlyIfAbsent:如果 true 代表不更改现有的值
- evict:如果为false表示 table 为创建状态
putVal 方法源代码如下所示:
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
static final int hash(Object key) {
int h;// 如果key是null 则hash值为0,否则调用key的hashCode()方法,并让高16位参与整个hash异或,如果数组长度比较小的情况下,让高16位也参与寻址,
// 路由寻址公式:(length - 1) & hash
// 这样可以使计算出的结果更分散,不容易产生哈希冲突
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
/*
1)transient Node<K,V>[] table; 表示存储Map集合中元素的数组。
2)(tab = table) == null 表示将空的table赋值给tab,然后判断tab是否等于null,第一次肯定是null(懒加载,new出map没有put值)。
3)(n = tab.length) == 0 表示将数组的长度0赋值给n,然后判断n是否等于0,n等于0,由于if判断使用双或,满足一个即可,则执行代码 n = (tab = resize()).length; 进行数组初始化,并将初始化好的数组长度赋值给n。
4)执行完n = (tab = resize()).length,数组tab每个空间都是null。
*/
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
/*
1)i = (n - 1) & hash 表示计算数组的索引赋值给i,即确定元素存放在哪个桶中。
2)p = tab[i = (n - 1) & hash]表示获取计算出的位置的数据赋值给结点p。
3) (p = tab[i = (n - 1) & hash]) == null 判断结点位置是否等于null,如果为null,则执行代码:tab[i] = newNode(hash, key, value, null);根据键值对创建新的结点放入该位置的桶中。
小结:如果当前桶没有哈希碰撞冲突,则直接把键值对插入空间位置。
*/
if ((p = tab[i = (n - 1) & hash]) == null)
// 创建一个新的结点存入到桶中
tab[i] = newNode(hash, key, value, null);
else {
// 执行else说明tab[i]不等于null,表示这个位置已经有值了
Node<K,V> e; K k;
/*
比较桶中第一个元素(数组中的结点)的hash值和key是否相等
1)p.hash == hash :p.hash表示原来存在数据的hash值 hash表示后添加数据的hash值 比较两个hash值是否相等。
说明:p表示tab[i],即 newNode(hash, key, value, null)方法返回的Node对象。
Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) {
return new Node<>(hash, key, value, next);
}
而在Node类中具有成员变量hash用来记录着之前数据的hash值的。
2)(k = p.key) == key :p.key获取原来数据的key赋值给k key 表示后添加数据的key比较两个key的地址值是否相等。
3)key != null && key.equals(k):能够执行到这里说明两个key的地址值不相等,那么先判断后添加的key是否等于null,如果不等于null再调用equals方法判断两个key的内容是否相等。
*/
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
/*
说明:两个元素哈希值相等,并且key的值也相等,
将旧的元素整体对象赋值给e,用e来记录
*/
e = p;
// hash值不相等或者key不相等;判断p是否为红黑树结点
else if (p instanceof TreeNode)
// 放入树中
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// 说明是链表结点
else {
/*
1)如果是链表的话需要遍历到最后结点然后插入
2)采用循环遍历的方式,判断链表中是否有重复的key
*/
for (int binCount = 0; ; ++binCount) {
/*
1)e = p.next 获取p的下一个元素赋值给e。
2)(e = p.next) == null 判断p.next是否等于null,等于null,说明p没有下一个元素,那么此时到达了链表的尾部,还没有找到重复的key,则说明HashMap没有包含该键,将该键值对插入链表中。
*/
if ((e = p.next) == null) {
/*
1)创建一个新的结点插入到尾部
p.next = newNode(hash, key, value, null);
Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) {
return new Node<>(hash, key, value, next);
}
注意第四个参数next是null,因为当前元素插入到链表末尾了,那么下一个结点肯定是null。
2)这种添加方式也满足链表数据结构的特点,每次向后添加新的元素。尾插法
*/
p.next = newNode(hash, key, value, null);
/*
1)结点添加完成之后判断此时结点个数是否大于TREEIFY_THRESHOLD临界值8,如果大于则将链表转换为红黑树。
2)int binCount = 0 :表示for循环的初始化值。从0开始计数。记录着遍历结点的个数。值是0表示第一个结点,1表示第二个结点。。。。7表示第八个结点,加上数组中的的一个元素,元素个数是9。
TREEIFY_THRESHOLD - 1 --》8 - 1 ---》7
如果binCount的值是7(加上数组中的的一个元素,元素个数是9)
TREEIFY_THRESHOLD - 1也是7,此时转换红黑树。
*/
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
// 转换为红黑树
treeifyBin(tab, hash);
// 跳出循环
break;
}
/*
执行到这里说明e = p.next 不是null,不是最后一个元素。继续判断链表中结点的key值与插入的元素的key值是否相等。
*/
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
// 相等,跳出循环
/*
要添加的元素和链表中的存在的元素的key相等了,则跳出for循环。不用再继续比较了
直接执行下面的if语句去替换去 if (e != null)
*/
break;
/*
说明新添加的元素和当前结点不相等,继续查找下一个结点。
用于遍历桶中的链表,与前面的e = p.next组合,可以遍历链表
*/
p = e;
}
}
/*
表示在桶中找到key值、hash值与插入元素相等的结点
也就是说通过上面的操作找到了重复的键,所以这里就是把该键的值变为新的值,并返回旧值
这里完成了put方法的修改功能
*/
if (e != null) {
// 记录e的value
V oldValue = e.value;
// onlyIfAbsent为false或者旧值为null
if (!onlyIfAbsent || oldValue == null)
// 用新值替换旧值
// e.value 表示旧值 value表示新值
e.value = value;
// 访问后回调
afterNodeAccess(e);
// 返回旧值
return oldValue;
}
}
// 修改记录次数
++modCount;
// 判断实际大小是否大于threshold阈值,如果超过则扩容
if (++size > threshold)
resize();
// 插入后回调
afterNodeInsertion(evict);
return null;
}
流程:
(1)计算key的hash值;
(2)如果桶(数组)数量为0,则初始化桶;
(3)如果key所在的桶没有元素,则直接插入;
(4)如果key所在的桶中的第一个元素的key与待插入的key相同,说明找到了元素,转后续流程(9)处理;
(5)如果第一个元素是树节点,则调用树节点的putTreeVal()寻找元素或插入树节点;
(6)如果不是以上三种情况,则遍历桶对应的链表查找key是否存在于链表中;
(7)如果找到了对应key的元素,则转后续流程(9)处理;
(8)如果没找到对应key的元素,则在链表最后插入一个新节点并判断是否需要树化;
(9)如果找到了对应key的元素,则判断是否需要替换旧值,并直接返回旧值;
(10)如果插入了元素,则数量加1并判断是否需要扩容;
扩容方法 resize()
扩容机制:
1.什么时候才需要扩容?
当HashMap中的元素个数超过 数组大小(长度)* loadFactor(负载因子) 时,就回进行数组扩容,loadFactor的默认值是0.75
2.HashMap的扩容是什么?
进行扩容,会伴随着一次重新hash分配,并且会遍历hash表中的所有数据,是非常耗时的,在编写程序中,要尽量避免resize。
HashMap在进行扩容是,使用的rehash方式非常巧妙,因为每次扩容都是翻倍,与原来计算的(n-1)& hash的结果相比,只是多了一个bit位,所以节点要么就是在原来的位置,要么就是被分配到 原位置+旧容量 这个位置。
例如我们从 16 扩展为 32 时,具体的变化如下所示:

说明:
5 是假设计算出来的原来的索引。这样就验证了上述所描述的:扩容之后所以结点要么就在原来的位置,要么就被分配到 “原位置 + 旧容量” 这个位置。
因此,我们在扩充 HashMap 的时候,不需要重新计算 hash,只需要看看原来的 hash 值新增的那个 bit 是 1 还是 0 就可以了,是 0 的话索引没变,是 1 的话索引变成 “原位置 + 旧容量” 。可以看看下图为 16 扩充为 32 的 resize 示意图:

正是因为这样巧妙的 rehash 方式,既省去了重新计算 hash 值的时间,而且同时,由于新增的 1bit 是 0 还是 1 可以认为是随机的,在 resize 的过程中保证了 rehash 之后每个桶上的结点数一定小于等于原来桶上的结点数,保证了 rehash 之后不会出现更严重的 hash 冲突,均匀的把之前的冲突的结点分散到新的桶中了。
源码 resize 方法的解读
/**
* 为什么需要扩容呢?
* 为了解决哈希冲突导致的链化影响查询效率问题,扩容会缓解该问题
*/
final Node<K,V>[] resize() {
// oldTab:表示扩容前的哈希表数组
Node<K,V>[] oldTab = table;
// oldCap:表示扩容之前table数组长度
// 如果当前哈希表数组等于null 长度返回0,否则返回当前哈希表数组的长度
int oldCap = (oldTab == null) ? 0 : oldTab.length;
// oldThr:表示扩容之前的阀值(触发本次扩容的阈值) 默认是12(16*0.75)
int oldThr = threshold;
// newCap:扩容之后的table散列表数组长度
// newThr: 扩容之后,下次再出发扩容的条件(新的扩容阈值)
int newCap, newThr = 0;
// 如果老的哈希表数组长度oldCap > 0
// 如果该条件成立,说明hashMap 中的散列表数组已经初始化过了,是一次正常扩容
// 开始计算扩容后的大小
if (oldCap > 0) {
// 扩容之前的table数组大小已经达到 最大阈值后,则不再扩容
// 且设置扩容条件为:int的最大值
if (oldCap >= MAXIMUM_CAPACITY) {
// 修改阈值为int的最大值
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 扩容之前的table数组大小没超过最大值,则扩充为原来的2倍
// (newCap = oldCap << 1) < MAXIMUM_CAPACITY 扩大到2倍之后容量要小于最大容量
// oldCap >= DEFAULT_INITIAL_CAPACITY 原哈希表数组长度大于等于数组初始化长度16
// 如果oldCap 小于默认初始容量16,比如传入的默认容量为8,则不执行下面代码
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
// 新的扩容阈值扩大一倍
newThr = oldThr << 1; // double threshold
}
// 如果老的哈希表数组长度oldCap == 0
// 说明hashMap中的散列表还没有初始化,这时候是null
// 如果老阈值oldThr大于0 直接赋值
/*
以下三种情况会直接进入该判断:(即,这时候oldThr扩容阈值已存在)
1.new HashMap(initCap,loadFactor);
2.new HashMap(initCap);
3.new HashMap(Map);// 这个传入的map中已经有数据
*/
else if (oldThr > 0) // 老阈值赋值给新的数组长度
newCap = oldThr;
// 如果老的哈希表数组长度oldCap == 0
// 说明hashMap中的散列表还没有初始化,这时候是null
// 此时,老扩容阈值oldThr == 0
else { // 直接使用默认值
newCap = DEFAULT_INITIAL_CAPACITY;//16
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);//12
}
// 如果执行到这个位置新的扩容阈值newThr还没有得到赋值,则
// 需要计算新的resize最大上限
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
// 将新的阀值newThr赋值给threshold
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
// 创建新的散列表
// newCap是新的数组长度---> 32
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
// 说明:hashMap本次扩容之前,table不为null
if (oldTab != null) {
// 把每个bucket桶的数据都移动到新的散列表中
// 遍历旧的哈希表的每个桶,重新计算桶里元素的新位置
for (int j = 0; j < oldCap; ++j) {
// 当前node节点
Node<K,V> e;
// 说明:此时的当前桶位中有数据,但是数据具体是
// 1.单个数据 、 2.还是链表 、 3.还是红黑树 并不能确定
if ((e = oldTab[j]) != null) {
// 原来的数据赋值为null 便于GC回收
oldTab[j] = null;
// 第一种情况:判断数组是否有下一个引用(是否是单个数据)
if (e.next == null)
// 没有下一个引用,说明不是链表,
// 当前桶上只有单个数据的键值对,
// 可以将数据直接放入新的散列表中
// e.hash & (newCap - 1) 寻址公式得到的索引结果有两种:
// 1.和原来旧散列表中的索引位置相同,
// 2.原来旧散列表中的索引位置i + 旧容量oldCap
newTab[e.hash & (newCap - 1)] = e;
//第二种情况:桶位已经形成红黑树
else if (e instanceof TreeNode)
// 说明是红黑树来处理冲突的,则调用相关方法把树分开
// 红黑树这块,我会单独写一篇博客给大家详细分析一下
// 红黑树相关可以先跳过
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
// 第三种情况:桶位已经形成链表
else { // 采用链表处理冲突
// 低位链表:
// 扩容之后数组的下标位置,与当前数组的下标位置一致 时使用
Node<K,V> loHead = null, loTail = null;
// 高位链表:扩容之后数组的下标位置等于
// 当前数组下标位置 + 扩容之前数组的长度oldCap 时使用
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
// 通过上述讲解的原理来计算结点的新位置
do {
// 原索引
next = e.next;
// 这里来判断如果等于true
// e这个结点在resize之后不需要移动位置
// 举例:
// 假如hash1 -> ...... 0 1111
// 假如oldCap=16 -> ...... 1 0000
// e.hash & oldCap 结果为0,则
// 扩容之后数组的下标位置j,与当前数组的下标位置一致
// 使用低位链表
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
// 举例:
// 假如hash2 -> ...... 1 1111
// 假如oldCap=16 -> ...... 1 0000
// e.hash & oldCap 结果不为0,则
// 扩容之后数组的下标位置为:
// 当前数组下标位置j + 扩容之前数组的长度oldCap
// 使用高位链表
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
// 将低位链表放到bucket桶里
if (loTail != null) {
loTail.next = null;
// 索引位置=当前数组下标位置j
newTab[j] = loHead;
}
// 将高位链表放到bucket里
if (hiTail != null) {
hiTail.next = null;
// 索引位置=当前数组下标位置j + 扩容之前数组的长度oldCap
newTab[j + oldCap] = hiHead;
}
}
}
}
}
// 返回新散列表
return newTab;
}
(1)如果使用是默认构造方法,则第一次插入元素时初始化为默认值,容量为16,扩容门槛为12;
(2)如果使用的是非默认构造方法,则第一次插入元素时初始化容量等于扩容门槛,扩容门槛在构造方法里等于传入容量向上最近的2的n次方;
(3)如果旧容量大于0,则新容量等于旧容量的2倍,但不超过最大容量2的30次方,新扩容门槛为旧扩容门槛的2倍;
(4)创建一个新容量的桶;
(5)搬移元素,原链表分化成两个链表,低位链表存储在原来桶的位置,高位链表搬移到原来桶的位置加旧容量的位置;
查找元素方法get()
查找方法,通过元素的 key 找到 value
代码如下:
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
get 方法主要调用的是 getNode 方法,代码如下:
final Node<K,V> getNode(int hash, Object key) {
// tab:引用当前hashMap的散列表
// first:桶位中的头元素
// e:临时node元素
// n:table数组的长度
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// 如果哈希表不为空,并且key对应的桶不为空
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
/*
判断数组元素是否相等
根据索引的位置检查第一个元素
注意:总是检查第一个元素
*/
// 第一种情况:定位出来的桶位元素 就是我们要get的数据
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// 桶位第一个元素不是我们要找的目标元素,且first.next不为null
// 说明当前桶位不止一个元素,可能是链表,也可能是红黑树
if ((e = first.next) != null) {
// 第二种情况:桶位已经升级成了红黑树
// 判断是否是红黑树,是的话调用红黑树中的getTreeNode方法获取结点
if (first instanceof TreeNode)
// 调用与树相关的方法得到目标元素
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
// 第三种情况:桶位已经形成链表
do {
// 不是红黑树的话,那就是链表结构了
// 通过循环的方法判断链表中是否存在该key
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
// 如果没找到返回null
return null;
}
小结:
get 方法实现的步骤:
a. 通过 hash 值获取该 key 映射到的桶
b. 桶上的 key 就是要查找的 key,则直接找到并返回
c. 桶上的 key 不是要找的 key,则查看后续的结点:
- 如果后续结点是红黑树结点,通过调用红黑树的方法根据 key 获取 value
- 如果后续结点是链表结点,则通过循环遍历链表根据 key 获取 value
删除方法 remove()
删除方法就是首先先找到元素的位置,如果是链表就遍历链表找到元素之后删除。如果是用红黑树就遍历树然后找到之后做删除,树小于 6 的时候要转链表。
删除 remove() 方法:
// remove方法的具体实现在removeNode方法中,所以我们重点看下removeNode方法
// 根据key删除
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
// 根据key,value 删除
@Override
public boolean remove(Object key, Object value) {
return removeNode(hash(key), key, value, true, true) != null;
}
removeNode() :
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
// 参数:
// matchValue 当根据 key和value 删除的时候该参数为true
// movable 可以先不用考虑这个参数
// tab:引用当前haashMap中的散列表
// p:当前node元素
// n:当前散列表数组长度
// index:表示寻址结果
Node<K,V>[] tab; Node<K,V> p; int n, index;
// 根据hash找到位置
// 如果当前key映射到的桶不为空
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
// 进入这个if判断内部,说明桶位是有数据的,需要进行查询操作,并且执行删除
// node:通过查找得到的要删除的元素
// e:表示当前node的下一个元素
// k,v 键 值
Node<K,V> node = null, e; K k; V v;
// 第一种情况:当前桶位中的元素 即为我们要删除的元素
// 如果桶上的结点就是要找的key,则将node指向该结点
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
// 如果桶位中的头一个元素不是我们要找的元素,且桶位中的e = p.next不为null
// 说明该桶位中的节点存在下一个节点
else if ((e = p.next) != null) {
// 说明:当前桶位,要么是 链表,要么是 红黑树
// 第二种情况:判断桶位中是否已经形成了红黑树
if (p instanceof TreeNode)
// 说明是以红黑树来处理的冲突,则获取红黑树要删除的结点
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
// 第三种情况:桶位中已经形成链表
else {
// 判断是否以链表方式处理hash冲突
// 是的话则通过遍历链表来寻找要删除的结点
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
// 比较找到的key的value和要删除的是否匹配
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
// 第一种情况:如果桶位中是红黑树,通过调用红黑树的方法来删除结点
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
// 第二种情况:如果桶位中是链表
else if (node == p)
// 链表删除
tab[index] = node.next;
// 如果桶位中
else
// 第三种情况:将当前元素p的下一个元素设置为 要删除元素的 下一个元素
p.next = node.next;
// 记录修改次数
++modCount;
// 变动的数量
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}
4.遍历HashMap的几种方式
分别遍历 Key 和 Values
for (String key : map.keySet()) {
System.out.println(key);
}
for (Object vlaue : map.values() {
System.out.println(value);
}
使用 Iterator 迭代器迭代
Iterator<Map.Entry<String, Object>> iterator = map.entrySet().iterator();
while (iterator.hasNext()) {
Map.Entry<String, Object> mapEntry = iterator.next();
System.out.println(mapEntry.getKey() + "---" + mapEntry.getValue());
}
通过 get 方式(不建议使用)
Set<String> keySet = map.keySet();
for (String str : keySet) {
System.out.println(str + "---" + map.get(str));
}
说明:
根据阿里开发手册,不建议使用这种方式,因为迭代两次。keySet 获取 Iterator一次,还有通过 get 又迭代一次,降低性能。
jdk8 以后使用 Map 接口中的默认方法:
default void forEach(BiConsumer<? super K,? super V> action)
// BiConsumer接口中的方法:
void accept(T t, U u) 对给定的参数执行此操作。
参数
t - 第一个输入参数
u - 第二个输入参数
遍历代码:
HashMap<String,String> map = new HashMap();
map.put("001", "zhangsan");
map.put("002", "lisi");
map.forEach((key, value) -> {
System.out.println(key + "---" + value);
});
总结:
- HashMap是一种散列表,1.8以后采用(数组+链表+红黑树)的存储结构
- HashMap的默认初始容量为16(1<<4),默认的负载因子是0.75f,容量总是2的n次方
- HashMap扩容时每次容量变为原来的2倍
- 当桶的数量小于64的时候不会进行树化,只会扩容
- 当桶的数量大于64且单个桶中的元素的数量大于8时,进行树化
- 当单个桶中的元素数量小于6时,进行反树化
- HashMap是非线程安全的容器
- HashMap查找添加元素的时间复杂度都是O(1)
hashSet和treeset有什么区别:
hashset是由一个hash表来实现的,因此它的元素是无序的,add,remove,contains方法的时间复杂度是 O(1)
treeset是由一个树形结构来实现的,它里面的元素是有序的,因此,add,remove,contains方法的时间复杂度是 O(logn)
红黑树
1.相关概念
二叉树:树的每个节点最多只能有两个子节点。
二叉搜索树:若它的左子树不为空,则左子树上所有节点的值均小于它的根节点的值;
若它的右子树不为空,则右子树上所有节点的值均大于它的根节点的值。
普通二叉搜索树致命缺陷:
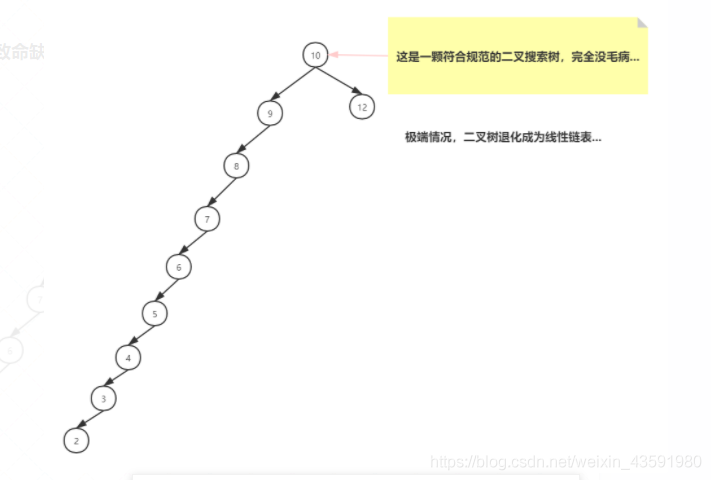
这颗二叉树查询效率咋样呢?
O(N)
怎么解决 二叉搜索树 退化成线性链表的问题?
如果插入元素时,树可以自动调整两边平衡,会保持不错的查找性能。
AVL树有什么特点?
- 1、具有二叉查找树的全部特性。
- 2、每个节点的左子树和右子树的高度差至多等于1
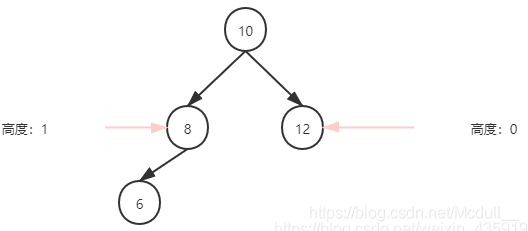
平衡树基于这种特点就可以保证不会出现大量节点偏向于一边的情况了!(插入或者删除时,会发生左旋、右旋操作,使这棵树再次左右保持一定的平衡)
为什么有了平衡树还需要红黑树?
虽然平衡树解决了二叉查找树退化为近似链表的缺点,能够把查找时间控制在 O(logn),不过却不是最佳的,因为平衡树要求每个节点的左子树和右子树的高度差至多等于1,这个要求实在是太严了,导致每次进行插入/删除节点的时候,几乎都会破坏平衡树的第二个规则,进而我们都需要通过左旋和右旋来进行调整,使之再次成为一颗符合要求的平衡树。
显然,如果在那种插入、删除很频繁的场景中,平衡树需要频繁着进行调整,这会使平衡树的性能大打折扣,为了解决这个问题,于是有了红黑树!!!
红黑树原理讲解:
红黑树的性质:
| 红黑树的性质 |
|---|
| 性质1:每个节点要么是黑色,要么是红色。 |
| 性质2:根节点是黑色。 |
| 性质3:每个叶子节点(NIL)是黑色。 |
| 性质4:每个红色节点的两个子节点一定都是黑色。不能有两个红色节点相连。 |
| 性质5:任意一节点到每个叶子节点的路径都包含数量相同的黑结点。俗称:黑高! |
红黑树实例图:
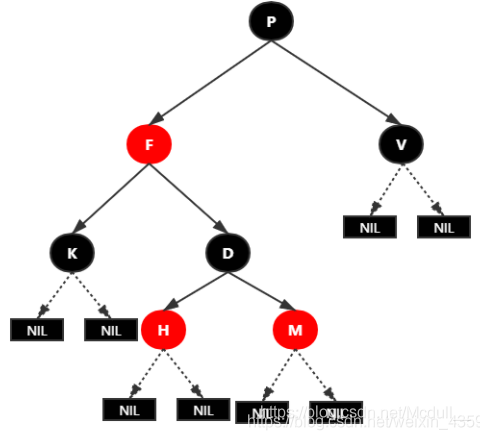
红黑树并不是一个完美平衡二叉查找树,从图上可以看到,根结点P的左子树显然比右子树高,
但左子树和右子树的黑结点的层数是相等的,也就是说,任意一个结点到到每个叶子结点的路径都包含数量相同的黑结点(性质5)。
所以我们叫红黑树这种平衡为黑色完美平衡。
前面讲到红黑树能自平衡,它靠的是什么?
三种操作:左旋、右旋和变色。
变色:结点的颜色由红变黑或由黑变红。
左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
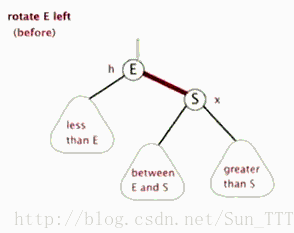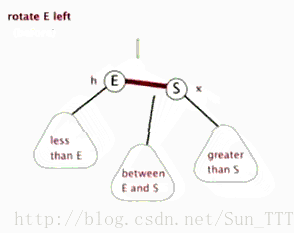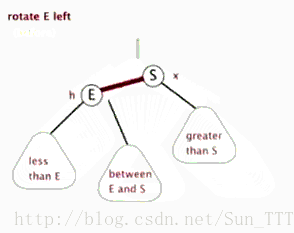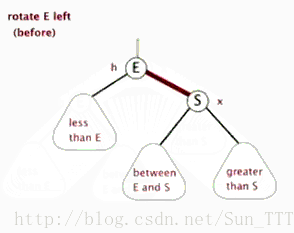
右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变
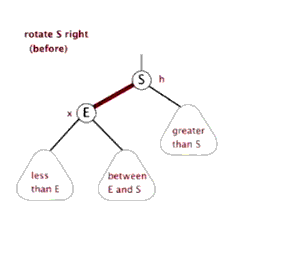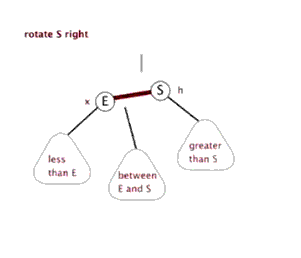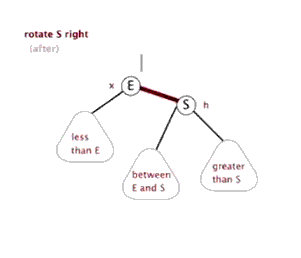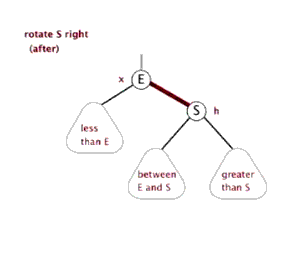
红黑树插入:
插入操作包括两部分工作:
1.查找插入的位置
2.插入后自平衡
注意:插入节点,必须为红色,理由很简单,红色在父节点(如果存在)为黑色节点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。但如果插入结点是黑色,那么插入位置所在的子树黑色结点总是多1,必须做自平衡。
2.插入情景模拟:
情景1:红黑树为空树
最简单的一种情景,直接把插入结点作为根结点就行
注意:根据红黑树性质2:根节点是黑色。还需要把插入结点设为黑色。
情景2:插入结点的Key已存在
处理:更新当前节点的值,为插入节点的值
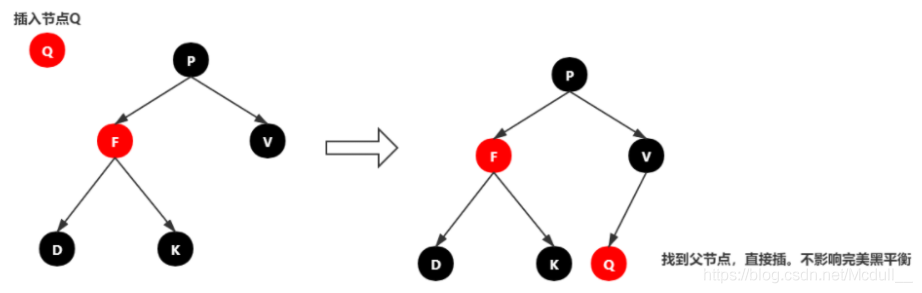
情景3:插入结点的父结点为黑结点
由于插入的结点是红色的,当插入结点的黑色时,并不会影响红黑树的平衡,直接插入即可,无需做自平衡。
情景4:插入节点的父节点为红色
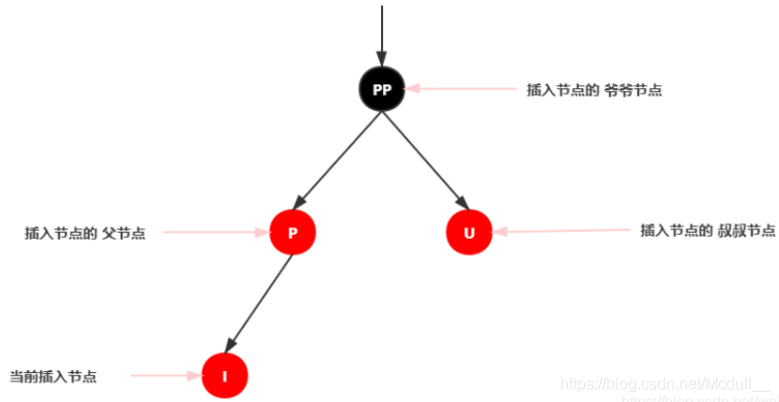
再次回想下红黑树的性质2:根结点是黑色。如果插入节点的父结点为红结点,那么该父结点不可能为根结点,所以插入结点总是存在祖父结点。
这一点很关键,因为后续的旋转操作肯定需要祖父结点的参与。
插入情景4.1:叔叔结点存在并且为红结点
依据红黑树性质4可知,红色节点不能相连 ==> 祖父结点肯定为黑结点;
因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是:黑红红。显然最简单的处理方式是把其改为:红黑红
处理:
1.将P和U节点改为黑色
2.将PP改为红色
3.将PP设置为当前节点,进行后续处理
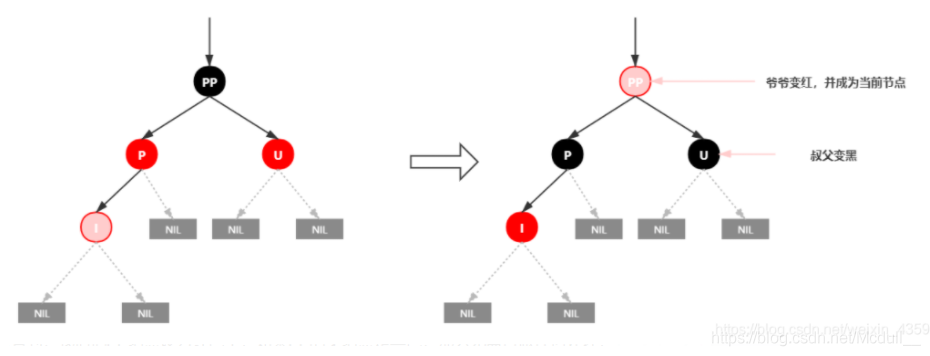
可以看到,我们把PP结点设为红色了,如果PP的父结点是黑色,那么无需再做任何处理;
但如果PP的父结点是红色,则违反红黑树性质了。所以需要将PP设置为当前节点,继续做插入操作自平衡处理,直到平衡为止。
插入情景4.2:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点
注意:单纯从插入前来看,叔叔节点非红即空(NIL节点),否则的话破坏了红黑树性质5,此路径会比其它路径多一个黑色节点。
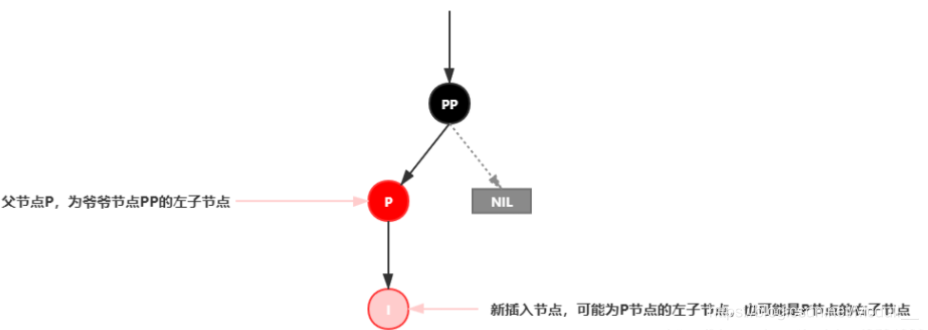
插入情景4.2.1:新插入节点,为其父节点的左子节点(LL红色情况)
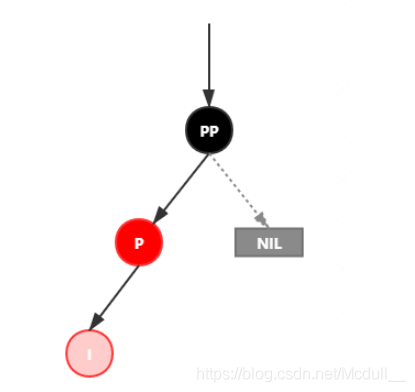
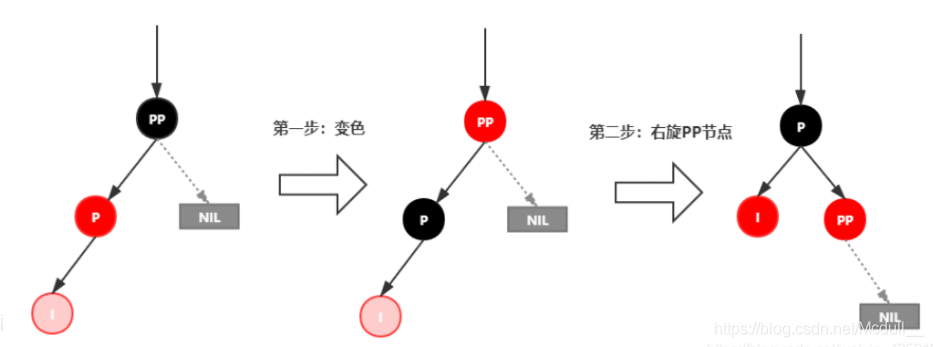
处理:
1.变颜色:将P设置为黑色,将PP设置为红色
2.对PP节点进行右旋
插入情景4.2.2:新插入节点,为其父节点的右子节点(LR红色情况)
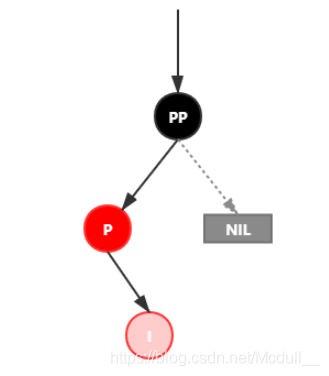
处理:
1.对P进行左旋
2.将P设置为当前节点,得到LL红色情况
3.按照LL红色情况处理(1.变颜色 2.右旋PP)
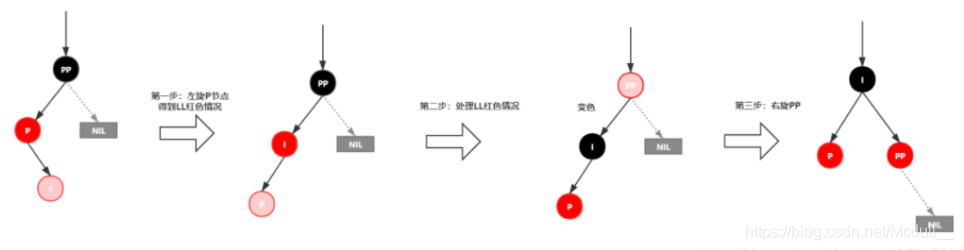
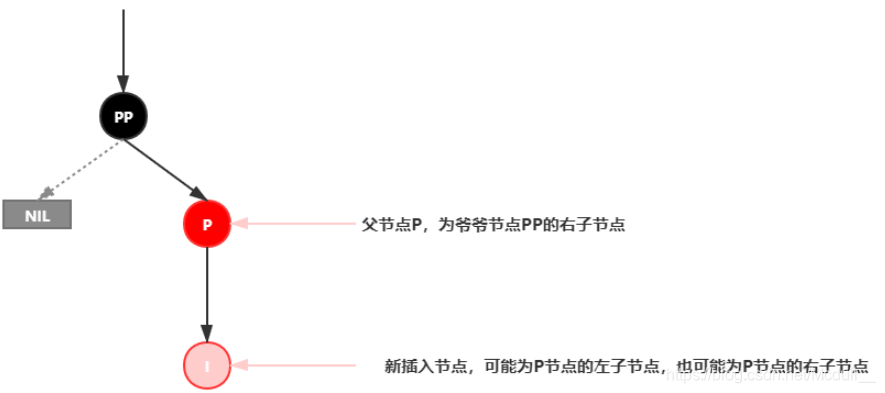
插入情景4.3:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的右子结点
该情景对应情景4.2,只是方向反转,直接看图。
插入情景4.3.1:新插入节点,为其父节点的右子节点(RR红色情况)
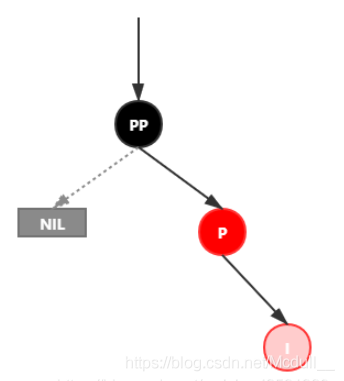
处理:
1.变颜色:将P设置为黑色,将PP设置为红色
2.对PP节点进行左旋
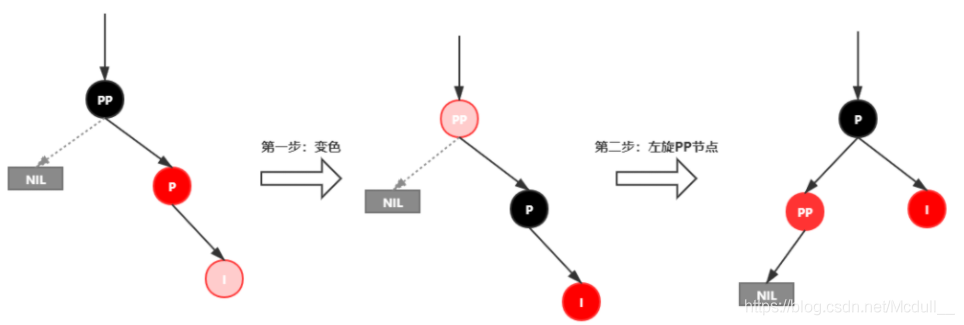
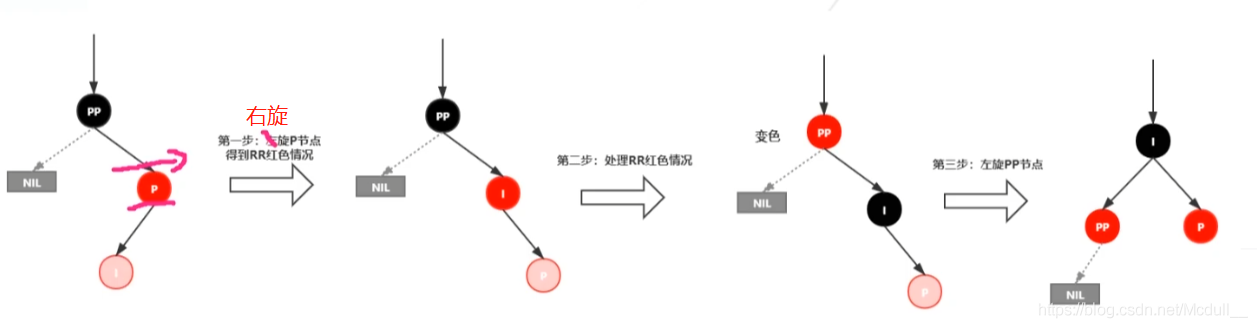
插入情景4.3.2:新插入节点,为其父节点的左子节点(RL红色情况)
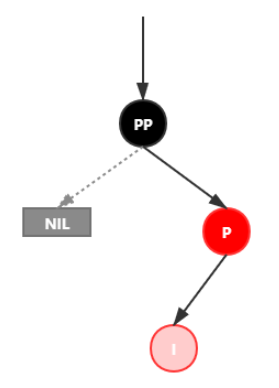
处理:
1.对P进行右旋
2.将P设置为当前节点,得到RR红色情况
3.按照RR红色情况处理(1.变颜色 2.左旋PP)
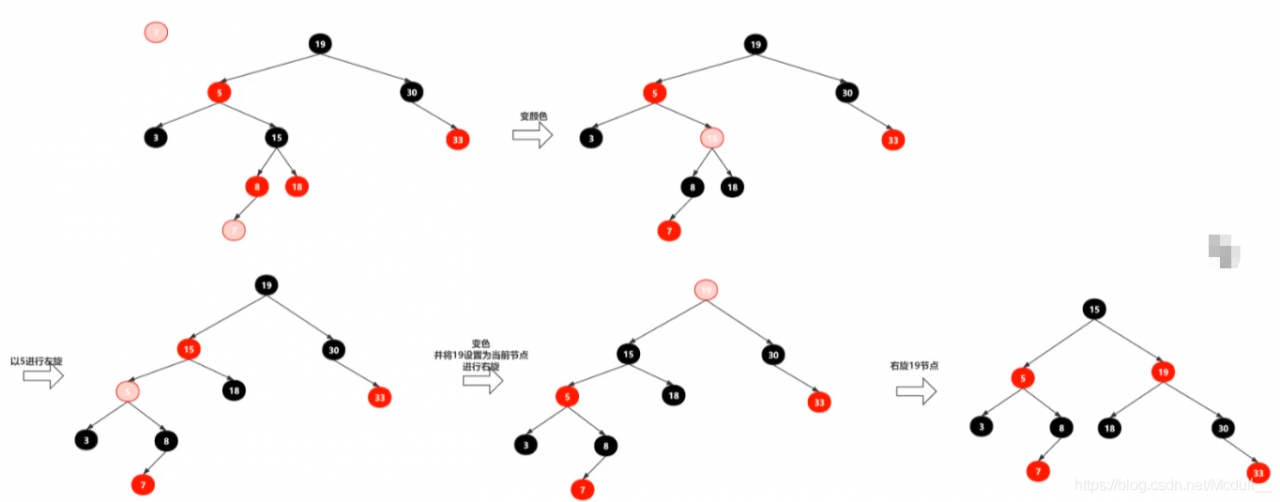
综合案例:
3.手撕红黑树

①创建RBTree,定义颜色
②创建RBNode
③辅助方法定义:parentOf(node),isRed(node),setRed(node),setBlack(node),inOrderPrint()
④左旋方法定义:leftRotate(node)
⑤右旋方法定义:rightRotate(node)
⑥公开插入接口方法定义:insert(K key, V value);
⑦内部插入接口方法定义:insert(RBNode node);
⑧修正插入导致红黑树失衡的方法定义:insertFIxUp(RBNode node);
⑨测试红黑树正确性
代码案例:
RBTree.java
package com.haust.map;
/**
* @Description: ①创建RBTree,定义颜色
* <p>
* ②创建RBNode
* <p>
* ③辅助方法定义:parentOf(node),isRed(node),setRed(node),setBlack(node),inOrderPrint()
* <p>
* ④左旋方法定义:leftRotate(node)
* <p>
* ⑤右旋方法定义:rightRotate(node)
* <p>
* ⑥公开插入接口方法定义:insert(K key, V value);
* <p>
* ⑦内部插入接口方法定义:insert(RBNode node);
* <p>
* ⑧修正插入导致红黑树失衡的方法定义:insertFIxUp(RBNode node);
* <p>
* ⑨测试红黑树正确性
*/
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;// 红
private static final boolean BLACK = false;// 黑
/**
* 树根的引用
**/
private RBNode root;
public RBNode getRoot() {
return root;
}
/**
* 获取当前节点的父节点
*
* @param node
* @return
*/
private RBNode parentOf(RBNode node) {
if (node != null) {
return node.parent;
}
return null;
}
/**
* 节点是否为红色
*
* @param node
* @return
*/
private boolean isRed(RBNode node) {
if (node != null) {
return node.color == RED;
}
return false;
}
/**
* 节点是否为黑色
*
* @param node
* @return
*/
private boolean isBlack(RBNode node) {
if (node != null) {
return node.color == BLACK;
}
return false;
}
/**
* 设置节点为红色
*
* @param node
*/
private void setRed(RBNode node) {
if (node != null) {
node.color = RED;
}
}
/**
* 设置节点为黑色
*
* @param node
*/
private void setBlack(RBNode node) {
if (node != null) {
node.color = BLACK;
}
}
/**
* 中序打印二叉树
*/
public void inOrderPrint() {
inOrderPrint(this.root);
}
private void inOrderPrint(RBNode node) {
if (node != null) {
inOrderPrint(node.left);
System.out.println("key:" + node.key + ",value:" + node.value);
inOrderPrint(node.right);
}
}
/**
* 左旋方法
* 左旋示意图:左旋x节点
* p p
* | |
* x y
* / \ ----> / \
* lx y x ry
* / \ / \
* ly ry lx ly
*
* 左旋做了几件事?
* 1.将x的右子节点指向y的左子节点(ly),并且把y的左子节点更新为x
* 2.当x的父节点(不为空时),更新y的父节点为x的父节点,并将x的父节点 指定 子树(当前x的子树位置) 指定为y
* 3.将x的父节点更新为y,将y的左子节点更新为x
*/
private void leftRotate(RBNode x) {
RBNode y = x.right;// 获得y
// 1.将x的右子节点指向y的左子节点(ly),并且把y的左子节点更新为x
x.right = y.left;
if (y.left != null) {
y.left.parent = x;
}
// 2.当x的父节点(不为空时),更新y的父节点为x的父节点,并将x的父节点 指定 子树(当前x的子树位置) 指定为y
if (x.parent != null) {
y.parent = x.parent;
if (x == x.parent.left) {// 如果x是其父节点的左子节点,则将y放在x父节点的左边
x.parent.left = y;
} else {
x.parent.right = y;// 如果x是其父节点的右子节点,则将y放在x父节点的右边
}
} else {// 说明x为根节点,此时需要更新y为根节点 的引用
this.root = y;
this.root.parent = null;// 根节点无父节点
}
// 3.将x的父节点更新为y,将y的左子节点更新为x
x.parent = y;
y.left = x;
}
/**
* 右旋方法
* 右旋示意图:右旋y节点
*
* p p
* | |
* y x
* / \ ----> / \
* x ry lx y
* / \ / \
* lx ly ly ry
*
* 右旋都做了几件事?
* 1.将y的左子节点指向x的右子节点,并且更新x的右子节点的父节点为y
* 2.当y的父节点不为空时,更新x的父节点为y的父节点,更新y的父节点的指定子节点(y当前位置) 为x
* 3.更新y 的父节点为x ,更新x 的右子节点为y
*/
private void rightRotate(RBNode y) {
RBNode x = y.left;// 获得 x
// 1.将x的右子节点 赋值 给了 y 的左子节点,并且更新x的右子节点的父节点为 y
y.left = x.right;
if(x.right != null) {
x.right.parent = y;
}
// 2.将y的父节点p(非空时)赋值给x的父节点,同时更新p的子节点为x(左或右)
if(y.parent != null) {
x.parent = y.parent;
if(y.parent.left == y) {// 如果y是其父节点的左子节点,则将x放在y父节点的左边
y.parent.left = x;
} else {// 如果y是其父节点的右子节点,则将x放在y父节点的右边
y.parent.right = x;
}
} else {// 说明y为根节点,此时需要更新x为根节点 的引用
this.root = x;
this.root.parent = null;// 根节点无父节点
}
// 3.将x的右子节点赋值为y,将y的父节点设置为x
x.right = y;
y.parent = x;
}
/**
* public插入方法
*
* @param key
* @param value
*/
public void insert(K key, V value) {
RBNode node = new RBNode<>();
node.setKey(key);
node.setValue(value);
// 新节点 一定要是红色!
node.setColor(RED);
insert(node);
}
private void insert(RBNode node) {
// 第一步:查找当前要插入节点node的父节点
RBNode parent = null;// 声明要插入节点node的父节点
RBNode x = this.root;
while (x != null) {
parent = x;
/**
* cmp > 0 说明node.key 大于 x.key 需要到x 的右子树查找
* cmp == 0 说明node.key 等于 x.key 需要进行替换操作
* cmp < 0 说明node.key 小于 x.key 需要到x 的左子树查找
*/
int cmp = node.key.compareTo(x.key);
if (cmp > 0) {
x = x.right;
} else if (cmp == 0) {
x.setValue(node.getValue());
return;// 修改完后 就不再继续往下面的代码执行了
} else {
x = x.left;
}
}
/**
* 退出上面的while循环后,到这里,说明树中没有相同key 的元素
*
* 需要添加新元素node到 x(parent) 目前位置的左子树/右子树
*/
node.parent = parent;
if (parent != null) {
// 判断node与parent 的key 谁大
int cmp = node.key.compareTo(parent.key);
if (cmp > 0) {// 当前node的key比parent 的key大,需要把node放入parent 的右子节点
parent.right = node;
} else {// 当前node的key比parent 的key小,需要把node放入parent 的左子节点
parent.left = node;
}
} else {// parent == null; 说明为空树
this.root = node;// 直接给树根赋值为node
}
// 新元素node 加入树中之后,要调用修复红黑树平衡的方法
insertFixUp(node);
}
/**
* 插入后修复红黑树平衡的方法
* |---情景1:如果红黑树为空树,需要将根节点染为黑色
* |---情景2:如果插入节点的key已经存在,(这种情况不需要处理,因为修改树中的值不会触发红黑树修复平衡方法)
* |---情景3:如果插入节点的父节点为黑色,这种情况不需要处理,(参考红黑树的性质4和性指5去理解)
* (因为所插入的路径中,黑色节点数没发生变化,所以红黑树依然平衡)
* <p>
* 情景4 需要去处理的情景
* |---情景4:插入节点的父节点为红色,(违反红黑树性质4,不能有两个红色节点相连)
* |---情景4.1:叔叔节点存在,并且为红色(父-叔 双红)
* 处理:将爸爸和叔叔染成黑色,将爷爷染成红色,并且再以爷爷节点为当前节点,进行下一轮处理
* |---情景4.2:叔叔节点不存在,或者为黑色,父节点为爷爷节点的左子树
* 处理:
* |---情景4.2.1:插入节点为其父节点的左子节点(LL情况)
* 处理:将父节点染为黑色,将爷爷染为红色,然后以爷爷节点右旋即可
* |---情景4.2.2:插入节点为其父节点的右子节点(LR情况)
* 处理:将父节点进行一次左旋,得到LL双红情景(4.2.1),然后指定父节点为当前节点进行下一轮处理
* |---情景4.3:叔叔节点不存在,或者为黑色,父节点为爷爷节点的右子树
* |---情景4.3.1:插入节点为其父节点的右子节点(RR情况)
* 处理:将父节点染为黑色,将爷爷节点染为红色,然后以爷爷节点左旋即可
* |---情景4.3.2:插入节点为其父节点的左子节点(RL情况)
* 处理:以父节点进行一次右旋,得到RR双红情景(4.3.1),然后指定父节点为当前节点进行下一轮处理
*/
private void insertFixUp(RBNode node) {
RBNode parent = parentOf(node);// 当前节点的父节点
RBNode gparent = parentOf(parent);// 当前节点的爷爷节点
// 存在父节点且父节点为红色
if (parent != null && isRed(parent)) {
// 父节点是红色的,那么一定存在爷爷节点(性质2:根节点只能是黑色)
// 父节点为爷爷节点的左子树
if (parent == gparent.left) {
RBNode uncle = gparent.right;
// 情景4.1:叔叔节点存在,并且为红色(父-叔 双红)
// 将父和叔染色为黑色,再将爷爷染红,并将爷爷设置为当前节点,进入下一次循环判断
if (uncle != null && isRed(uncle)) {
setBlack(parent);
setBlack(uncle);
setRed(gparent);
insertFixUp(gparent);
return;
}
// 情景4.2:叔叔节点不存在,或者为黑色,父节点为爷爷节点的左子树
if (uncle == null || isBlack(uncle)) {
/**
* 情景4.2.1:插入节点为其父节点的左子节点(LL情况)
* 处理:将父节点染为黑色,将爷爷染为红色,然后以爷爷节点右旋即可
*/
// 插入节点为其父节点的左子节点(LL情况)=>
// 变色(父节点变黑,爷爷节点变红),右旋爷爷节点
if (node == parent.left) {
setBlack(parent);
setRed(gparent);
rightRotate(gparent);// 以gparent 右旋
}
/**
* 情景4.2.2:插入节点为其父节点的右子节点(LR情况)
* 处理:将父节点进行一次左旋,得到LL双红情景(4.2.1),然后指定父节点为当前节点进行下一轮处理
*/
// 插入节点为其父节点的右子节点(LR情况)=>
// 左旋(父节点),当前节点设置为父节点,进入下一次循环
if (node == parent.right) {
leftRotate(parent);// parent 左旋
insertFixUp(parent);// 进行下一轮处理
return;
}
}
} else {// 父节点为爷爷节点的右子树
RBNode uncle = gparent.left;
// 情景4.1:叔叔节点存在,并且为红色(父-叔 双红)
// 将父和叔染色为黑色,再将爷爷染红,并将爷爷设置为当前节点,进入下一次循环判断
if (uncle != null && isRed(uncle)) {
setBlack(parent);
setBlack(uncle);
setRed(gparent);
insertFixUp(gparent);// 进行下一轮处理
return;
}
// 情景4.3:叔叔节点不存在,或者为黑色,父节点为爷爷节点的右子树
if (uncle == null || isBlack(uncle)) {
/**
* 情景4.3.1:插入节点为其父节点的右子节点(RR情况)
* 处理:将父节点染为黑色,将爷爷节点染为红色,然后以爷爷节点左旋即可
*/
// 插入节点为其父节点的右子节点(RR情况)=>
// 变色(父节点变黑,爷爷节点变红),右旋爷爷节点
if (node == parent.right) {
setBlack(parent);
setRed(gparent);
leftRotate(gparent);
}
/**
* 情景4.3.2:插入节点为其父节点的左子节点(RL情况)
* 处理:以父节点进行一次右旋,得到RR双红情景(4.3.1),然后指定父节点为当前节点进行下一轮处理
*/
// 插入节点为其父节点的左子节点(RL情况)
// 右旋(父节点)得到RR情况,当前节点设置为父节点,进入下一次循环
if (node == parent.left) {
rightRotate(parent);
insertFixUp(parent);
return;
}
}
}
}
setBlack(this.root);
}
// 静态内部类
static class RBNode<K extends Comparable<K>, V> {
private RBNode parent;// 父节点
private RBNode left;// 左子树
private RBNode right;// 右子树
private boolean color;// 颜色
private K key;// 键
private V value;// 值
public RBNode(RBNode parent, RBNode left, RBNode right, boolean color, K key, V value) {
this.parent = parent;
this.left = left;
this.right = right;
this.color = color;
this.key = key;
this.value = value;
}
public RBNode() {
}
public RBNode getParent() {
return parent;
}
public void setParent(RBNode parent) {
this.parent = parent;
}
public RBNode getLeft() {
return left;
}
public void setLeft(RBNode left) {
this.left = left;
}
public RBNode getRight() {
return right;
}
public void setRight(RBNode right) {
this.right = right;
}
public boolean isColor() {
return color;
}
public void setColor(boolean color) {
this.color = color;
}
public K getKey() {
return key;
}
public void setKey(K key) {
this.key = key;
}
public V getValue() {
return value;
}
public void setValue(V value) {
this.value = value;
}
}
}
代码测试:
这里在网上找的一个打印红黑树的工具类:
TreeOperation.java
package com.haust.map;
/**
* @Description: 打印红黑树的工具类
*/
public class TreeOperation {
/*
树的结构示例:
1
/ \
2 3
/ \ / \
4 5 6 7
*/
// 用于获得树的层数
public static int getTreeDepth(RBTree.RBNode root) {
return root == null ? 0 : (1 + Math.max(getTreeDepth(root.getLeft()), getTreeDepth(root.getRight())));
}
private static void writeArray(RBTree.RBNode currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
// 保证输入的树不为空
if (currNode == null) return;
// 先将当前节点保存到二维数组中
res[rowIndex][columnIndex] = String.valueOf(currNode.getKey() /*+ "-" + (currNode.isColor() ? "R" : "B") + ""*/);
// 计算当前位于树的第几层
int currLevel = ((rowIndex + 1) / 2);
// 若到了最后一层,则返回
if (currLevel == treeDepth) return;
// 计算当前行到下一行,每个元素之间的间隔(下一行的列索引与当前元素的列索引之间的间隔)
int gap = treeDepth - currLevel - 1;
// 对左儿子进行判断,若有左儿子,则记录相应的"/"与左儿子的值
if (currNode.getLeft() != null) {
res[rowIndex + 1][columnIndex - gap] = "/";
writeArray(currNode.getLeft(), rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
}
// 对右儿子进行判断,若有右儿子,则记录相应的"\"与右儿子的值
if (currNode.getRight() != null) {
res[rowIndex + 1][columnIndex + gap] = "\\";
writeArray(currNode.getRight(), rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
}
}
public static void show(RBTree.RBNode root) {
if (root == null) System.out.println("EMPTY!");
// 得到树的深度
int treeDepth = getTreeDepth(root);
// 最后一行的宽度为2的(n - 1)次方乘3,再加1
// 作为整个二维数组的宽度
int arrayHeight = treeDepth * 2 - 1;
int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
// 用一个字符串数组来存储每个位置应显示的元素
String[][] res = new String[arrayHeight][arrayWidth];
// 对数组进行初始化,默认为一个空格
for (int i = 0; i < arrayHeight; i++) {
for (int j = 0; j < arrayWidth; j++) {
res[i][j] = " ";
}
}
// 从根节点开始,递归处理整个树
// res[0][(arrayWidth + 1)/ 2] = (char)(root.val + '0');
writeArray(root, 0, arrayWidth / 2, res, treeDepth);
// 此时,已经将所有需要显示的元素储存到了二维数组中,将其拼接并打印即可
for (String[] line : res) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < line.length; i++) {
sb.append(line[i]);
if (line[i].length() > 1 && i <= line.length - 1) {
i += line[i].length() > 4 ? 2 : line[i].length() - 1;
}
}
System.out.println(sb.toString());
}
}
}
测试:
package com.haust.map;
import java.util.Scanner;
/**
* @Description: RBTree红黑树 测试
*/
public class RBTreeTest {
public static void main(String[] args) {
RBTree<String, Object> rbtree = new RBTree();
//测试输入:ijkgefhdabc
while(true) {
Scanner sc = new Scanner(System.in);
System.out.println("请输入key:");
String key = sc.next();
rbtree.insert(key, null);
TreeOperation.show(rbtree.getRoot());
}
}
}
测试依次输入:**i j k g e f h d a b c **
为什么输入字符而不是数字呢?
因为为了方便起见,RBTree比对节点大小时 直接使用的是 node.key.compareTo(parent.key);这个其实是按照字符串比对的! 所以,大家尽量使用 a,b,c,d,e,f,g,h,i…这种风格去测试!
请输入key:
i
i-B
请输入key:
j
i-B
\
j-R
请输入key:
k
j-B
/ \
i-R k-R
请输入key:
g
j-B
/ \
i-B k-B
/
g-R
请输入key:
e
j-B
/ \
g-B k-B
/ \
e-R i-R
请输入key:
f
j-B
/ \
g-R k-B
/ \
e-B i-B
\
f-R
请输入key:
h
j-B
/ \
g-R k-B
/ \
e-B i-B
\ /
f-R h-R
请输入key:
d
j-B
/ \
g-R k-B
/ \
e-B i-B
/ \ /
d-R f-R h-R
请输入key:
a
g-B
/ \
e-R j-R
/ \ / \
d-B f-B i-B k-B
/ /
a-R h-R
请输入key:
b
g-B
/ \
e-R j-R
/ \ / \
b-B f-B i-B k-B
/ \ /
a-R d-R h-R
请输入key:
c
g-B
/ \
e-B j-B
/ \ / \
b-R f-B i-B k-B
/ \ /
a-B d-B h-R
/
c-R
HashMap底层的红黑树
红黑树的时间复杂度为O(log n),与树的高度成正比。
结合之前自定义的红黑树RBTree 我们来看一下HashMap底层真正的红黑树TreeNode:
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent;// 父节点
TreeNode<K,V> left;// 左子树
TreeNode<K,V> right;// 右子树
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;// 颜色
/**
* 有参构造函数
*/
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
/**
* 获取红黑树的根节点
*/
final TreeNode<K,V> root() {
for (TreeNode<K,V> r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
}
/**
* 确保给定的根root是树的第一个节点
*/
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
...
}
/**
* 调用find方法查找.
*/
final TreeNode<K, V> getTreeNode(int h, Object k) {
// 从树的根节点开始查找
return ((parent != null) ? root() : this).find(h, k, null);
}
/**
* 从根节点出发查找具有给定哈希值和键的节点.从根节点出发
* 查找当前要插入节点node的父节点
*
* 经典二叉查找树的查找过程,先根据hash值比较,再根据key值比较决定是查左子树还是右子树。
*/
final TreeNode<K, V> find(int h, Object k, Class<?> kc) {
TreeNode<K, V> p = this;
do {
int ph, dir;
K pk;
TreeNode<K, V> pl = p.left, pr = p.right, q;
if ((ph = p.hash) > h)
// 左子树
p = pl;
else if (ph < h)
// 右子树
p = pr;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
// 找到了直接返回
return p;
else if (pl == null)
// hash相同但key不同,左子树为空查右子树
p = pr;
else if (pr == null)
// 右子树为空查左子树
p = pl;
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
// 通过compare方法比较key值的大小决定使用左子树还是右子树
p = (dir < 0) ? pl : pr;
else if ((q = pr.find(h, k, kc)) != null)
// 如果以上条件都不通过,则尝试在右子树查找
return q;
else
// 都没找到就在左子树查找
p = pl;
} while (p != null);
return null;
}
/**
* 用于在a 和 b 的hash值相等且不可比较时对插入进行排序
*/
static int tieBreakOrder(Object a, Object b) {
...
}
/**
* 对链表进行树化的方法
*(1)从链表的第一个元素开始遍历;
*(2)将第一个元素作为根节点;
*(3)其它元素依次插入到红黑树中,再做平衡;
*(4)将根节点移到链表第一元素的位置(因为平衡的时候根节点会改变);
*/
final void treeify(Node<K, V>[] tab) {
TreeNode<K, V> root = null;
for (TreeNode<K, V> x = this, next; x != null; x = next) {
next = (TreeNode<K, V>) x.next;
x.left = x.right = null;
// 第一个元素作为根节点且为黑节点,其它元素依次插入到树中再做平衡
if (root == null) {
x.parent = null;
x.red = false;
root = x;
} else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
// 从根节点查找元素插入的位置
for (TreeNode<K, V> p = root; ; ) {
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
// 如果最后没找到元素,则插入
TreeNode<K, V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 插入后平衡,默认插入的是红节点,在balanceInsertion()方法里
root = balanceInsertion(root, x);
break;
}
}
}
}
// 把根节点移动到链表的头节点,因为经过平衡之后原来的第一个元素不一定是根节点了
moveRootToFront(tab, root);
}
/**
* 对红黑树进行反树化的方法
*/
final Node<K,V> untreeify(HashMap<K,V> map) {
Node<K,V> hd = null, tl = null;
for (Node<K,V> q = this; q != null; q = q.next) {
Node<K,V> p = map.replacementNode(q, null);
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
return hd;
}
/**
* 向树种插入数据的方法
*(1)寻找根节点;
*(2)从根节点开始查找;
*(3)比较hash值及key值,如果都相同,直接返回,在putVal()方法中决定是否要替换value值;
*(4)根据hash值及key值确定在树的左子树还是右子树查找,找到了直接返回;
*(5)如果最后没有找到则在树的相应位置插入元素,并做平衡;
*/
final TreeNode<K, V> putTreeVal(HashMap<K, V> map, Node<K, V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
// 标记是否找到这个key的节点
boolean searched = false;
// 找到树的根节点
TreeNode<K, V> root = (parent != null) ? root() : this;
// 从树的根节点开始遍历
for (TreeNode<K, V> p = root; ; ) {
// dir=direction,标记是在左边还是右边
// ph=p.hash,当前节点的hash值
int dir, ph;
// pk=p.key,当前节点的key值
K pk;
if ((ph = p.hash) > h) {
// 当前hash比目标hash大,说明在左边
dir = -1;
}
else if (ph < h)
// 当前hash比目标hash小,说明在右边
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
// 两者hash相同且key相等,说明找到了节点,直接返回该节点
// 回到putVal()中判断是否需要修改其value值
return p;
else if ((kc == null &&
// 如果k是Comparable的子类则返回其真实的类,否则返回null
(kc = comparableClassFor(k)) == null) ||
// 如果k和pk不是同样的类型则返回0,否则返回两者比较的结果
(dir = compareComparables(kc, k, pk)) == 0) {
// 这个条件表示两者hash相同但是其中一个不是Comparable类型或者两者类型不同
// 比如key是Object类型,这时可以传String也可以传Integer,两者hash值可能相同
// 在红黑树中把同样hash值的元素存储在同一颗子树,这里相当于找到了这颗子树的顶点
// 从这个顶点分别遍历其左右子树去寻找有没有跟待插入的key相同的元素
if (!searched) {
TreeNode<K, V> q, ch;
searched = true;
// 遍历左右子树找到了直接返回
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
// 如果两者类型相同,再根据它们的内存地址计算hash值进行比较
dir = tieBreakOrder(k, pk);
}
TreeNode<K, V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
// 如果最后确实没找到对应key的元素,则新建一个节点
Node<K, V> xpn = xp.next;
TreeNode<K, V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K, V>) xpn).prev = x;
// 插入树节点后平衡
// 把root节点移动到链表的第一个节点
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
// remove 调用 removeNode
//public V remove(Object key) {
// Node<K, V> e;
// return (e = removeNode(hash(key), key, null, false, true)) == null ?
// null : e.value;
//}
final Node<K, V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K, V>[] tab;
Node<K, V> p;
int n, index;
// 如果桶的数量大于0且待删除的元素所在的桶的第一个元素不为空
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K, V> node = null, e;
K k;
V v;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// 如果第一个元素正好就是要找的元素,赋值给node变量后续删除使用
node = p;
else if ((e = p.next) != null) {
if (p instanceof TreeNode)
// 如果第一个元素是树节点,则以树的方式查找节点
node = ((TreeNode<K, V>) p).getTreeNode(hash, key);
else {
// 否则遍历整个链表查找元素
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
// 如果找到了元素,则看参数是否需要匹配value值,如果不需要匹配直接删除,
// 如果需要匹配则看value值是否与传入的value相等
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
if (node instanceof TreeNode)
// 如果是树节点,调用树的删除方法(以node调用的,是删除自己)
((TreeNode<K, V>) node).removeTreeNode(this, tab, movable);
else if (node == p)
// 如果待删除的元素是第一个元素,则把第二个元素移到第一的位置
tab[index] = node.next;
else
// 否则删除node节点
p.next = node.next;
++modCount;
--size;
// 删除节点后置处理
afterNodeRemoval(node);
return node;
}
}
return null;
}
/**
*(1)先查找元素所在的节点;
*(2)如果找到的节点是树节点,则按树的移除节点处理;
*(3)如果找到的节点是桶中的第一个节点,则把第二个节点移到第一的位置;
*(4)否则按链表删除节点处理;
*(5)修改size,调用移除节点后置处理等;
*/
final void removeTreeNode(HashMap<K, V> map, Node<K, V>[] tab,
boolean movable) {
int n;
// 如果桶的数量为0直接返回
if (tab == null || (n = tab.length) == 0)
return;
// 节点在桶中的索引
int index = (n - 1) & hash;
// 第一个节点,根节点,根左子节点
TreeNode<K, V> first = (TreeNode<K, V>) tab[index], root = first, rl;
// 后继节点,前置节点
TreeNode<K, V> succ = (TreeNode<K, V>) next, pred = prev;
if (pred == null)
// 如果前置节点为空,说明当前节点是根节点,则把后继节点赋值到第一个节点的位置,相当于删除了当前节点
tab[index] = first = succ;
else
// 否则把前置节点的下个节点设置为当前节点的后继节点,相当于删除了当前节点
pred.next = succ;
// 如果后继节点不为空,则让后继节点的前置节点指向当前节点的前置节点,相当于删除了当前节点
if (succ != null)
succ.prev = pred;
// 如果第一个节点为空,说明没有后继节点了,直接返回
if (first == null)
return;
// 如果根节点的父节点不为空,则重新查找父节点
if (root.parent != null)
root = root.root();
// 如果根节点为空,则需要反树化(将树转化为链表)
// 如果需要移动节点且树的高度比较小,则需要反树化
if (root == null
|| (movable
&& (root.right == null
|| (rl = root.left) == null
|| rl.left == null))) {
tab[index] = first.untreeify(map); // too small
return;
}
// 分割线,以上都是删除链表中的节点,下面才是直接删除红黑树的节点(因为TreeNode本身即是链表节点又是树节点)
// 删除红黑树节点的大致过程是寻找右子树中最小的节点放到删除节点的位置,然后做平衡,此处不过多注释
TreeNode<K, V> p = this, pl = left, pr = right, replacement;
if (pl != null && pr != null) {
TreeNode<K, V> s = pr, sl;
while ((sl = s.left) != null) // find successor
s = sl;
boolean c = s.red;
s.red = p.red;
p.red = c; // swap colors
TreeNode<K, V> sr = s.right;
TreeNode<K, V> pp = p.parent;
if (s == pr) { // p was s's direct parent
p.parent = s;
s.right = p;
} else {
TreeNode<K, V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
p.left = null;
if ((p.right = sr) != null)
sr.parent = p;
if ((s.left = pl) != null)
pl.parent = s;
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
if (sr != null)
replacement = sr;
else
replacement = p;
} else if (pl != null)
replacement = pl;
else if (pr != null)
replacement = pr;
else
replacement = p;
if (replacement != p) {
TreeNode<K, V> pp = replacement.parent = p.parent;
if (pp == null)
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;
}
TreeNode<K, V> r = p.red ? root : balanceDeletion(root, replacement);
if (replacement == p) { // detach
TreeNode<K, V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
if (movable)
moveRootToFront(tab, r);
}
/**
* Splits nodes in a tree bin into lower and upper tree bins,
* or untreeifies if now too small. Called only from resize;
* see above discussion about split bits and indices.
*
* @param map the map
* @param tab the table for recording bin heads
* @param index the index of the table being split
* @param bit the bit of hash to split on
*/
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
...
}
// 左旋
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;
if (p != null && (r = p.right) != null) {
if ((rl = p.right = r.left) != null)
rl.parent = p;
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}
// 右旋
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
// 修复红黑树平衡的方法
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
x.red = true;
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (!xp.red || (xpp = xp.parent) == null)
return root;
if (xp == (xppl = xpp.left)) {
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
else {
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
TreeNode<K,V> x) {
for (TreeNode<K,V> xp, xpl, xpr;;) {
if (x == null || x == root)
return root;
else if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (x.red) {
x.red = false;
return root;
}
else if ((xpl = xp.left) == x) {
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
xpr = (xp = x.parent) == null ? null : xp.right;
}
if (xpr == null)
x = xp;
else {
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
xpr.red = true;
x = xp;
}
else {
if (sr == null || !sr.red) {
if (sl != null)
sl.red = false;
xpr.red = true;
root = rotateRight(root, xpr);
xpr = (xp = x.parent) == null ?
null : xp.right;
}
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null)
sr.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
}
x = root;
}
}
}
else { // symmetric
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
/**
* Recursive invariant check
*/
static <K,V> boolean checkInvariants(TreeNode<K,V> t) {
TreeNode<K,V> tp = t.parent, tl = t.left, tr = t.right,
tb = t.prev, tn = (TreeNode<K,V>)t.next;
if (tb != null && tb.next != t)
return false;
if (tn != null && tn.prev != t)
return false;
if (tp != null && t != tp.left && t != tp.right)
return false;
if (tl != null && (tl.parent != t || tl.hash > t.hash))
return false;
if (tr != null && (tr.parent != t || tr.hash < t.hash))
return false;
if (t.red && tl != null && tl.red && tr != null && tr.red)
return false;
if (tl != null && !checkInvariants(tl))
return false;
if (tr != null && !checkInvariants(tr))
return false;
return true;
}
}
(1)TreeNode本身既是链表节点也是红黑树节点;
(2)先删除链表节点;
(3)再删除红黑树节点并做平衡;
将链表转换为红黑树 treeifyBin()
结点添加完成之后判断此时结点个数是否大于 TREEIFY_THRESHOLD 临界值 8,如果大于则将链表转换为红黑树,转换红黑树的方法 treeifyBin,整体代码如下:
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
//转换为红黑树 tab表示数组名 hash表示哈希值
treeifyBin(tab, hash);
treeifyBin 方法如下所示:
/*
替换指定哈希表的索引处桶中的所有链接结点,除非表太小,否则将修改大小。
Node<K,V>[] tab = tab 数组名
int hash = hash表示哈希值
*/
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
/*
如果当前数组为空或者数组的长度小于进行树形化的阈值(MIN_TREEIFY_CAPACITY = 64),
就去扩容。而不是将结点变为红黑树。
目的:如果数组很小,那么转换红黑树,然后遍历效率要低一些。这时进行扩容,
那么重新计算哈希值,链表长度有可能就变短了,数据会放到数组中,这样相对来说效率高一些。
*/
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
//扩容方法
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
/*
1)执行到这里说明哈希表中的数组长度大于阈值64,开始进行树形化
2)e = tab[index = (n - 1) & hash]表示将数组中的元素取出赋值给e,
e是哈希表中指定位置桶里的链表结点,从第一个开始
*/
// hd:红黑树的头结点 tl:红黑树的尾结点
TreeNode<K,V> hd = null, tl = null;
do {
// 新创建一个树的结点,内容和当前链表结点e一致
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p; // 将新创键的p结点赋值给红黑树的头结点
else {
p.prev = tl; // 将上一个结点p赋值给现在的p的前一个结点
tl.next = p; // 将现在结点p作为树的尾结点的下一个结点
}
tl = p;
/*
e = e.next 将当前结点的下一个结点赋值给e,如果下一个结点不等于null
则回到上面继续取出链表中结点转换为红黑树
*/
} while ((e = e.next) != null);
/*
让桶中的第一个元素即数组中的元素指向新建的红黑树的结点,以后这个桶里的元素就是红黑树
而不是链表数据结构了
*/
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}
小结:上述操作一共做了如下几件事:
- 根据哈希表中元素个数确定是扩容还是树形化。
- 如果是树形化遍历桶中的元素,创建相同个数的树形结点,复制内容,建立起联系。
- 然后让桶中的第一个元素指向新创建的树根结点,替换桶的链表内容为树形化内容。储在原来桶的位置,高位链表搬移到原来桶的位置加旧容量的位置。



