[聚类算法]聚类算法中的K-Means实现以及验证

K-Means聚类算法，感觉是接触到目前为止，距离程序员思维最近的算法，应该也是使用到的数理知识最简单的算法。
所以在记笔记的时候，忍不住，又去实现了一把，但是根据吴大大（吴恩达）的介绍来看，的确是不需要每个算法都自己去写的，而是需要了解的算法的本质、知道算法适用的场景，多加练习，才能达到熟能生巧的程度。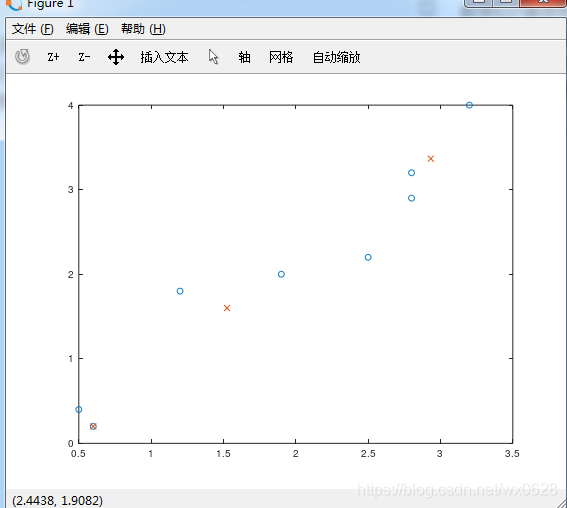

符号“o”表示数据点。符号“x”表示我们需要寻找的中心点。
主要思路描述：
1、在所有的点中随机选择K点（也就是中心点），详见函数中的getRandom（我在函数中增加了K点不重复的逻辑，如果重复的话，结果就变成K-1个点了）；
2、计算每个x点到第K个点的距离，假设我们x(i)，x有i个点；K(k)，K中心点有k个点；我们将x(i)分析给到第K个点距离最短的那个K点。也就是归属到哪个K点的势力范围；
3、我们计算每个K点的势力范围下面的x(i)的点，并计算在该势力范围的中位点。并将K点移动到对位的中位点。
然后再重复2、3步骤，直到最终K点不再移动。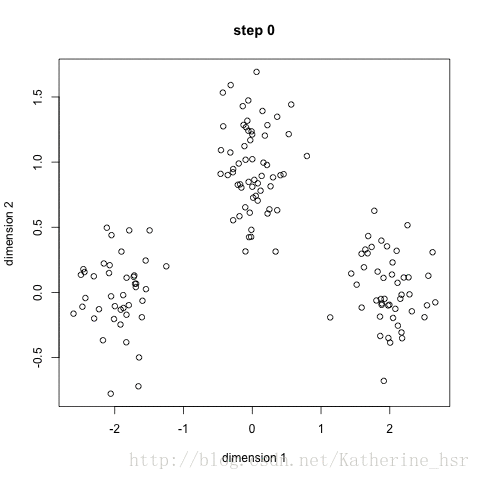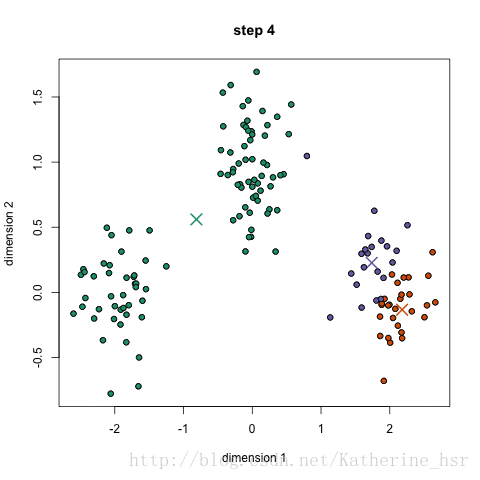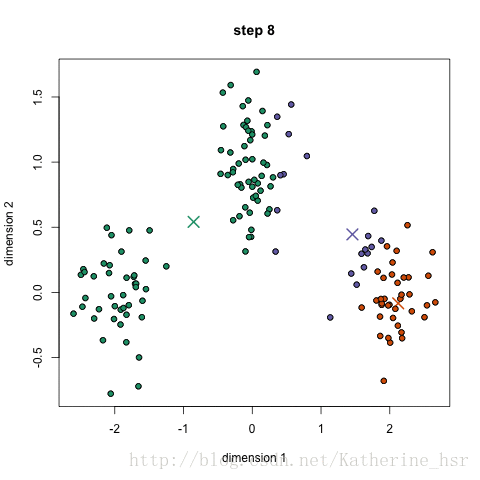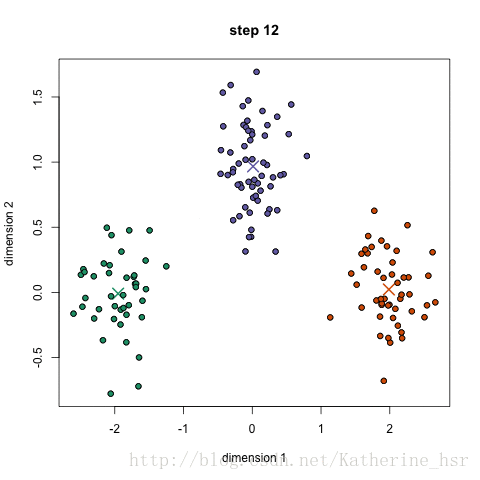

注：图片借用网友的图（原文章地址：https://blog.csdn.net/Katherine_hsr/article/details/79382249）
是一篇比较综合来讲聚类算法的文档。

根据上述的分析来看代码的实现：

%分类器，聚类算法（K-Means）
%入参：k,随机点K的个数，K=2,表示将所有的点分成两个簇cluster；
%入参：x,表示欲分类的记录集（x1,x2,x3...,xj）表示j个维度或者特征
%出参：K，表示每次分类选择的K点，形式如下：[k01,k02,..k0k;k11,k12,...kik],k表示族数，i表示循环选点的次数
function K = CluseringKmeans(k,x)
  %iCount代表样本数；
  %jCount代表特征数；
  iCount=size(x)(1);
  jCount=size(x)(2);
  %随机取点
  RandList = getRandom(iCount,k)
  K(:,:)=x(RandList,:)
  LastKean=mean(mean(K));
  KMeanErr = LastKean - 0;
  while abs(KMeanErr)>0,
    LastKean=mean(mean(K));
    %求所有x的点到L点的距离，然后选择最小的，放到C中去
    for iIndex = 1 : iCount,
      %用来记录最小的点
      minMixValue=0;
      %需要对每个点的到每个K值点的距离进行求解
      for kIndex = 1 : k,
        %如果K(i)与当前取值点是相同的，则距离等于0，这种情况下，不需要对计算
        if iIndex == RandList(kIndex,1),
          C(iIndex,1)=kIndex;
          break;
         elseif,
           tmpMix=x(iIndex,:)-K(kIndex,:);
           MixErr=tmpMix'*tmpMix;
           %如果minMixValue=0代表还没有赋值，直接使用当前点
           if minMixValue==0,
             minMixValue=MixErr;
           endif
           if MixErr<=minMixValue,
             C(iIndex,1)=kIndex;
           endif
        endif
      endfor    
    endfor
    %重新计算K点的均值
    
    for kIndex =1 :k,
     K(kIndex,:) = mean(x(find(C==kIndex),:),1);
    endfor
    %如果两点的K点已经固定，则退出循环
    KMeanErr=mean(mean(K))-LastKean;
  endwhile; 
endfunction

%返回随机数列表，列表中的随机数不重复
%入参：itop,表示随机数从1到iTop之间；
%入参：iNumberCount表示要生成多少个随机数
function randList = getRandom(itop,iNumberCount)
  randList = zeros(iNumberCount,1);
  iCernLen = 1 / itop;
  for iIndex = 1 : iNumberCount,
  %在iTop范围内，找一个不重复的Index
    bRepeat=false;
    while bRepeat == false,
      iTmpNum = floor(rand(1)/iCernLen);
      if iTmpNum==0,
        break;
      endif
      bRepeat=true;
      for rIndex = 1 : size(randList)(1),
        if iTmpNum == randList(rIndex,1),
            bRepeat = false;
            break;
        endif
      endfor      
     endwhile
     randList(iIndex,1)=iTmpNum;    
  endfor
endfunction

对上述代码进行验证：

x=[0.5,0.4;0.6,0.2;1.2,1.8;1.9,2.0;2.5,2.2;2.8,2.9;2.8,3.2;3.2,4.0;0.8,1.2;1.0,1.1;0.8,1.2;1.8,2.0;1.9,2.2;2.0,2.1]
plot(x(:,1),x(:,2),'o')
hold on
k=CluseringKmeans(1,3,x)
plot(k(:,1),k(:,2),'x')

得到的结果如下图所示：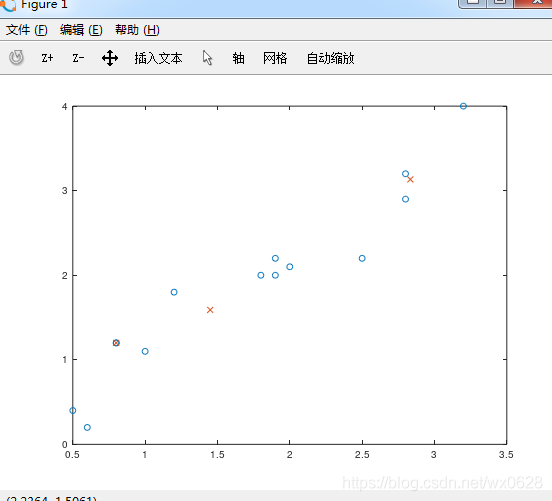

从上图来看，凭我们的直觉也会认为这并不是一个小的分类。
那么我们需要多次执行，综合去寻找一个比较好的结果。再多试几次试一下：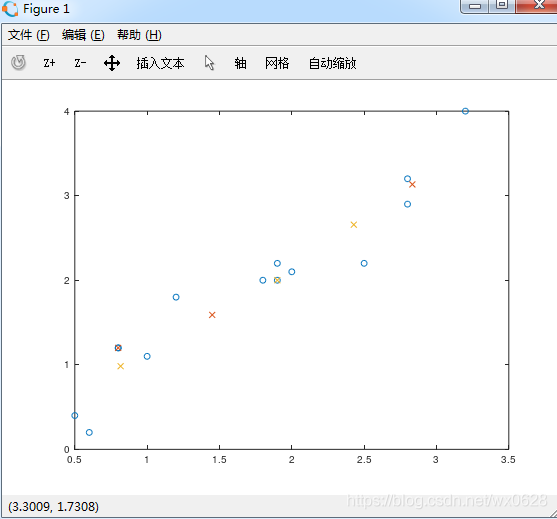

看淡橙的点，这个结果就比较符合我们的期望了。聚类算法的结果，目前还是需要多次执行来寻找一个最优解。