论文地址：Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition

一、核心思想

PGC认为卷积可认为是特定的取样函数（sample function）与特定的权重函数（weight function）相乘后求和。
论文中本模型作用于基于人体骨架的动作识别任务。

二、传统卷积对比

对于传统卷积，将一个$K\times K$的卷积核的卷积操作可以认为是以下函数：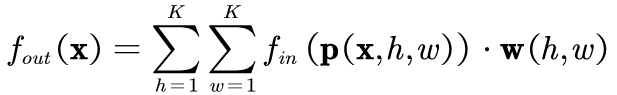

其中$K$是卷积核大小(常见3、5)。$p()$是一个取样函数，将节点从邻域依次取出，用于卷积计算。$w()$是权重函数，即对每个节点进行卷积操作的参数。
例如：对于$3\times 3$的卷积核，$k=3$，$p(x,1,1)$就是左上角的第一个点，$w(1,1)$代表卷积核上左上角的系数。

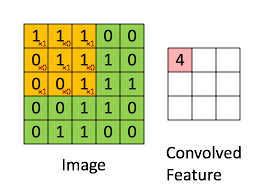
整个式子就是节点特征与卷积核参数的内积。

三、PGC实现

PGC就是将以上认为的卷积思想运用到图结构中，主要过程就是取一个合适的取样函数和一个对应的权重函数。

取样函数

取样函数即在邻域内依次取出节点。重点在于如何构建节点的邻域，也就是说取样函数在哪里取样。

在图结构数据上，PGC可以定义取样函数在D阶近邻的节点上。即$B\left(v_i\right)=\left\{v_j\mid d\left(v_j,v_i\right)\le D\right\}$，其中$d(v_j,v_i)$表示从$i$节点到$j$节点的最短距离。

在实验中取$D=1$，且在1阶邻域中挨个取样。但是也可以设置成其他的邻域。

权重函数

首先将取样的邻域内的点分为$K$个不同的类。
$$l_i:B(v_i)\to \{0,\dots ,K-1\}$$

其中$l_i(\cdot )$代表第$i$个节点的分类映射。$B(v_i)$表示第$i$个节点的邻域节点。$\{0,\dots ,K-1\}$代表类别。

相同的类共享一个卷积核参数。不同类之间的卷积核不共享参数：
$$w(v_i,v_j)=w^{\prime }(l_i(v_j))$$

表示$v_i,v_j$之间的卷积核参数等于他所属邻域类的卷积核。

分类策略

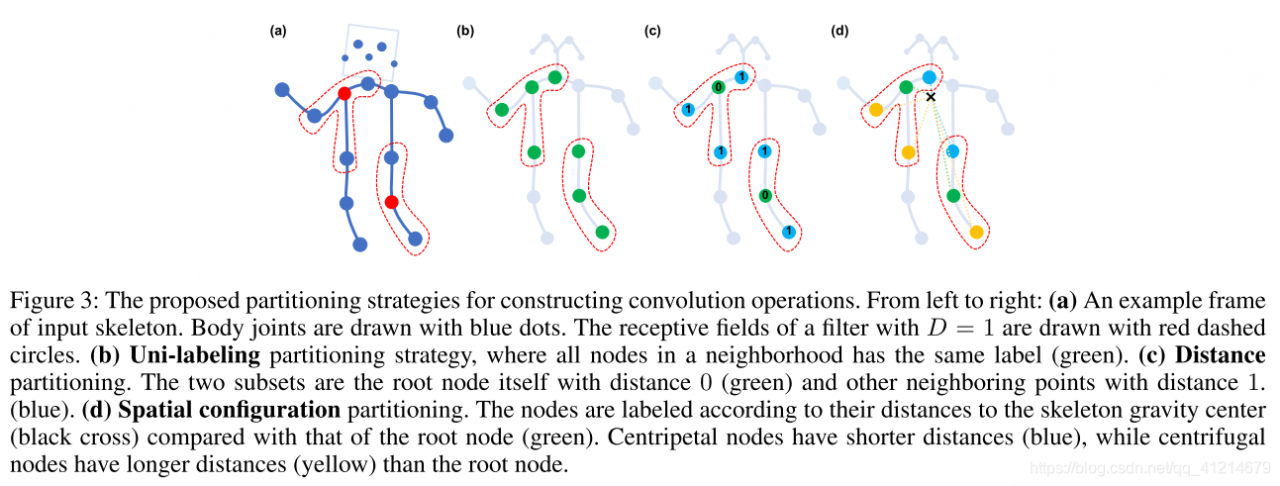
($a$):输入骨架的示例框架。身体的关节是用蓝点画的。$D=1$的过滤器的接受域用红色虚线圆圈绘制。红色节点为中心节点，圈内为其1阶邻域。

($b$):Uni-labeling分类
一视同仁，只有一个类别，类似GNN。

($c$):Distance分类
根据阶数来进行分类，中心节点为0阶，相邻节点为1阶，分为不同的类。

($d$):Spatial configuratio分类
根据与人体骨架中心的距离来分类，有三个类别。结点距离小于中心节点和骨架中心的距离的为一类，结点距离大于中心节点和骨架中心的距离的为一类，中心节点为一类。

公式

最终卷积公式如下：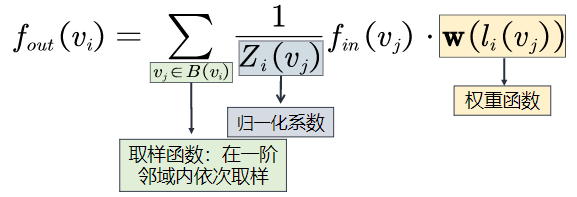

$Z_i(v_j)$的意义为在i节点邻域中$j$节点所属类别的节点数量(类别=$v_j$),用于平衡每一类节点信息。

对比思考

1.相较于GraphSAGE的均值采样，PGC定义了一个取样函数，泛化性更强。

2.GNN认为节点需要排序，GraphSAGE认为不需要排序，而PGC采用了权重函数，若只分为一个类别则类似于GNN，若认为每个节点类别不相同，那么就类似于GraphSAGE，具有更强的泛化。

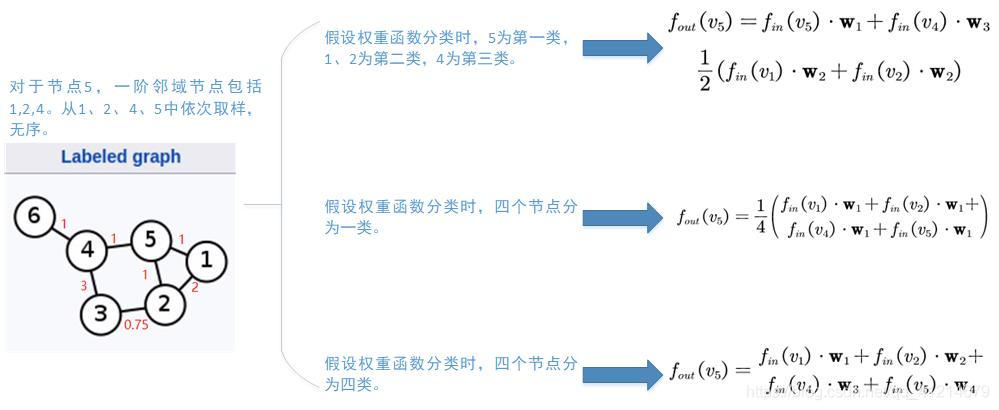
举例