系列文章目录
文章目录
一、什么是函数
1.函数是程序的重要组成部分,每个程序都必须有一个主函数。
2.人们往往编写一些函数,用来实现各种功能。
3.解题的过程就是调用和执行一系列函数的过程,一个函数就是一个功能。
二、函数的分类
1.系统函数
库函数
如sqrt,fabs等等,由系统提供,需要引头文件。
2.自定义函数
(1)无参函数
void print(void)
{
cout << "I love C++" << endl;
}
int main()
{
print();
return 0;
}
其中函数定义时括号中的void可缺省。
(2)有参函数
//写一个判断闰年的函数,是闰年返回1,不是闰年返回0。
int is_leap_year(int year)
{
if (((year % 4 == 0) && (year % 100 != 0)) || (year % 400 == 0))
return 1;
else
return 0;
}
int main()
{
int year;
cin >> year;
int ret = is_leap_year(year);
if (ret==1)
cout << "是闰年" << endl;
else
cout << "不是闰年" << endl;
}
三、函数的定义
1.定义无参函数
类型名 函数名([void])
{
声明部分
执行语句
}
2.定义有参函数
类型名 函数名(形式参数表列)
{
声明部分
执行语句
}
四、函数的参数
1.实际参数(实参):
真实传给函数的参数叫实参。
实参可以是:常量,变量,表达式,函数等。
无论实参是何种类型的量,在进行函数调用时,他们必须有确定的值,以便于把这些值传给形参。
2.形式参数(形参):
形式参数是指函数名后括号中的变量,形式参数当函数调用完成后就自动销毁了,因此形式参数只在函数中有效。
没调用函数时,就不会为形式参数分配内存空间。
五.函数的调用
1.传值调用
函数的形参和实参分别占用不同的内存块,对形参的修改不会影响实参。
2.传址调用
*传址调用时把函数外部创建变量的内存地址传给函数参数的一种函数调用方式。
*这种传参方式可以让函数和函数外边的变量建立起真正的联系,也就是函数内部可以直接作函数外部的变量。
3.区分两种调用
写一个函数交换两个整形变量
//传值调用
void swap(int x, int y)
{
int temp = x;
x = y;
y = temp;
}
int main()
{
int x = 1;
int y = 2;
swap(x, y);
cout << x << " " << y << endl;
return 0;
}
当函数调用的时候,实参传给形参,形参其实是实参的一份零时拷贝。所以对形参的修改,不会影响实参。
//传址调用
void swap(int* x, int* y)
{
int temp = *x;
*x = *y;
*y = temp;
}
int main()
{
int x = 1;
int y = 2;
swap(&x, &y);
cout << x << " " << y << endl;
return 0;
}
使用指针传址调用,对目标空间内的值进行修改,可以很好地完成任务。
六、函数的声明
如果使用自定义函数,而该函数与主调函数在一个程序单位中,且位置在主调函数之后则必须在调用此函数之前对被调用的函数做声明。
用一个函数求两函数之和
int main()
{
float add(float x, float y);
float x, y;
cin >> x >> y;
cout << add(x, y) << endl;
return 0;
}
float add(float x, float y)
{
return x + y;
}
函数声明也可不写形参名,只写形参的类型。
float add(float,float);
七、函数的嵌套调用
C++不允许对函数做嵌套定义,也就是说在一个函数中不能完整的包含另一个函数,但是可以嵌套调用。
在程序中实现函数嵌套调用时,需要注意的是:在调用函数之前,需要对每一个被调用函数作声明(除非定义在前调用在后)。
八、函数的递归调用
1.什么是递归?
程序调用自身的编程技巧称为递归。
递归作为一种算法在程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为与原问题相似的规模较小的问题来去解,递归策略只需用少量的程序就可描述出题解过程中所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思考方式在于:把大事化小
2.递归的两个必要条件
(1)存在限制条件,当满足这个限制条件时,递归便不再继续。
(2)每次递归调用之后越来越接近这个限制条件。
九、课后习题
122~123页
1.写两个函数,分别求两个整数的最大公约数和最小公倍数,用主函数调用两个函数,并输出结果,两个整数由键盘输入。
int LMC(int x, int y)
{
int z = x;
while (x % y)
{
x += z;
}
return x;
}
int GCD(int x, int y)
{
int z=0;
while (x % y)
{
z = x % y;
x = y;
y = z;
}
return z;
}
int main()
{
int x, y;
cin >> x >> y;
int ret1 = LMC(x, y);
int ret2 = GCD(x, y);
cout << "最小公倍数=" << ret1 << endl;
cout << "最大公约数=" << ret2 << endl;
return 0;
}
最小公倍数,用x除以y,只要余数不为0,x就加上它的初始值,余数为0时,x就是最小公倍数。
最大公约数,用了辗转相除法,用大数除以小数,把小数赋给大数,把余数赋给小数,如此进行下去。12和8:12%8=4,8%4=0,4为最大公约数。
2.求方程ax2 +bx+c=0的根,用3个函数分别求当b2-4ac大于0、等于0和小于0时的根,并输出结果。从主函数输入a,b,c的值。
void f1(float delta, float a, float b)
{
cout << "x1=" << (-b - sqrt(delta)) / (2 * a) << endl;
cout << "x2=" << (-b + sqrt(delta)) / (2 * a) << endl;
}
void f2( float a, float b)
{
cout << "x1=x2=" << (-b) / (2 * a) << endl;
}
void f3(float delta, float a, float b)
{
cout << "x1=" << -b / (2 * a) << "-" << sqrt(-delta) / (2 * a) <<"i" << endl;
cout << "x2=" << -b / (2 * a) << "+" << sqrt(-delta) / (2 * a) <<"i" << endl;
}
int main()
{
float a, b, c, delta;
cin >> a >> b >> c;
delta = b * b - 4 * a * c;
if (delta > 0)
f1(delta, a, b);
else if (delta == 0)
f2(a, b);
else
f3(delta, a, b);
return 0;
}
3.写一个判断素数的函数,在主函数中输入一个整数,输出是否为素数的信息。
void is_prime(int a)
{
for (int i = 2; i <= sqrt(a); i++)//不要漏掉“=”,不然9就错了。
{
if (a % i == 0)
{
cout << "不是素数" << endl;
return ;
}
}
cout << "是素数" << endl;
}
int main()
{
int a = 0;
cin >> a;
is_prime(a);
return 0;
}
4.求a!+b!+c!的值,用一个函数fac(n)求n!。a,b,c的值由主函数输入,最终得到的值在主函数中输出。
int fac(int n)
{
if (n == 1)
return 1;
else
return fac(n - 1) * n;
}
int main()
{
int a, b, c;
cin >> a >> b >> c;
cout << fac(a) + fac(b) + fac(c)<<endl;
return 0;
}
5.写一函数求sinh(x)的值,求sinh(x)的近似公式为sinh(x)=(ex-e-x)/2,其中用一个函数求ex。
float f(float x)
{
return (exp(x) - exp(-x)) / 2;
}
int main()
{
float x;
cin >> x;
cout << f(x) << endl;
return 0;
}
6.用牛顿迭代法求根。方程为ax3+bx2+cx+d=0。系数a,b,c,d的值依次为1,2,3,4,由主函数输入。求x在1附近的一个实根。求出根后由主函数输出。
double newton(double a, double b, double c, double d)
{
double x = 1;
double x0, f,f1;
do
{
x0 = x;
f = a * x0 * x0 * x0 + b * x0 * x0 + c * x0 + d;
f1 = 3 * a * x0 * x0 + 2 * b * x0 + c;
x = x0 - f / f1;
} while (fabs(x - x0) >= 1e-5);
return x;
}
int main()
{
int a, b, c, d;
cin >> a >> b >> c >> d;
double ret=newton(a, b, c, d);
cout << ret << endl;
return 0;
}
7.写一个函数验证哥德巴赫猜想:一个不小于6的偶数可以表示为两个素数之和,如6=3+3,8=3+5,10=3+7,…在主函数中输入一个不小于6的偶数n,然后调用函数gotbaha,在gotbaha函数中再调用prime函数,prime函数的作用是判别一个数是否为素数。在gotbaha函数中输出以下形式的结果:
34=3+31
int prime(int a)
{
for (int i = 2; i <= sqrt(a); i++)
{
if (a % i == 0)
{
return 1;//不是素数返回1
}
}
return 0;//是素数返回0
}
void gotbaha(int n)
{
int a, b;
a = b = n / 2;
while (prime(a) || prime(b))
{
a++;
b--;
}
cout << n << "=" << a << "+" << b << endl;
}
int main()
{
again:
int n;
cin >> n;
if ((n % 2 != 0) || n < 6)
{
cout << "请重新输入!" << endl;
goto again;
}
gotbaha(n);
goto again;
return 0;
}
8.用递归方法求n阶勒让德多项式的值,递归公式为
float p(int x,int n)
{
if (n == 0)
return 1;
else if (n == 1)
return x;
else if(n>1)
return (((2 * n - 1) * x * p(x, (n - 1)) - (n - 1) * p(x, (n - 2))) / n);
}
int main()
{
int x=0;
int n=0;
cin >> x >> n;
float ret=p(x,n);
cout << ret << endl;
return 0;
}
9.汉诺塔问题。这是一个经典的数学问题:古代有一个梵塔,塔内有3个座A,B,C,开始时A座上有64个盘子,盘子大小不等,大的在下小的在上。有一个老和尚想把这64个盘子从A座移动到C座,但每次只允许移动一个盘,且在移动过程中3个座上始终保持大盘在下,小盘在上。在移动过程中可以利用B座,要求编程序打印出移动的步骤。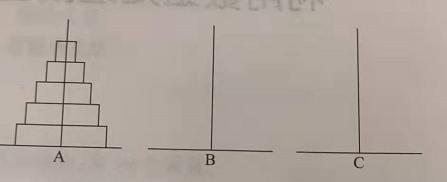
汉诺塔
10.用递归法将一个整数n转换成字符串。例如,输入483,应输出字符串"483"。n的位数不确定可以是任意位数的整数。
void convert(int n)
{
int i=n;
char ch;
if (n / 10 != 0)
convert(n / 10);
ch = i % 10 + '0';
cout << ch;
}
int main()
{
int n;
cin >> n;
convert(n);
return 0;
}
11.用递归法求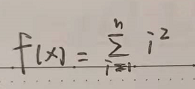
n的值由主函数输入。
int f(int n)
{
if (n == 0)
return 0;
else if (n == 1)
return 1;
else
return n * n + f(n - 1);
}
int main()
{
int n;
cin >> n;
int ret = f(n);
cout << ret << endl;
return 0;
}