前言
前两篇博客(从贝叶斯角度理解正则化、正则化)分别介绍了提前终止法和正则化法。

它们可以近似等价的吗?怎么近似等价?
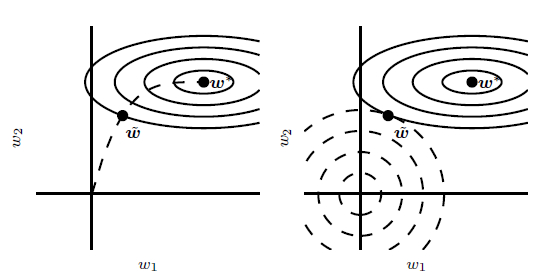
左边这张图轮廓线表示负对数似然函数的轮廓,虚线表示从原点开始的SGD所经过的轨迹。提前终止法的轨迹在较早的$\tilde \omega 点 终 止 , 而 不 是 在 停 止 在 最 小 化 代 价 的 点 点终止,而不是在停止在最小化代价的点点终止,而不是在停止在最小化代价的点{\omega ^{\text{*}}}$处;
右边这张图使用了L2正则化法。虚线圆圈表示L2惩罚的轮廓,L2惩罚使得总代价的最小值比非正则化代价的最小值更靠近原点。
可以看出,两种方法近似等价。
接下来对两者进行分析。
提前终止法分析
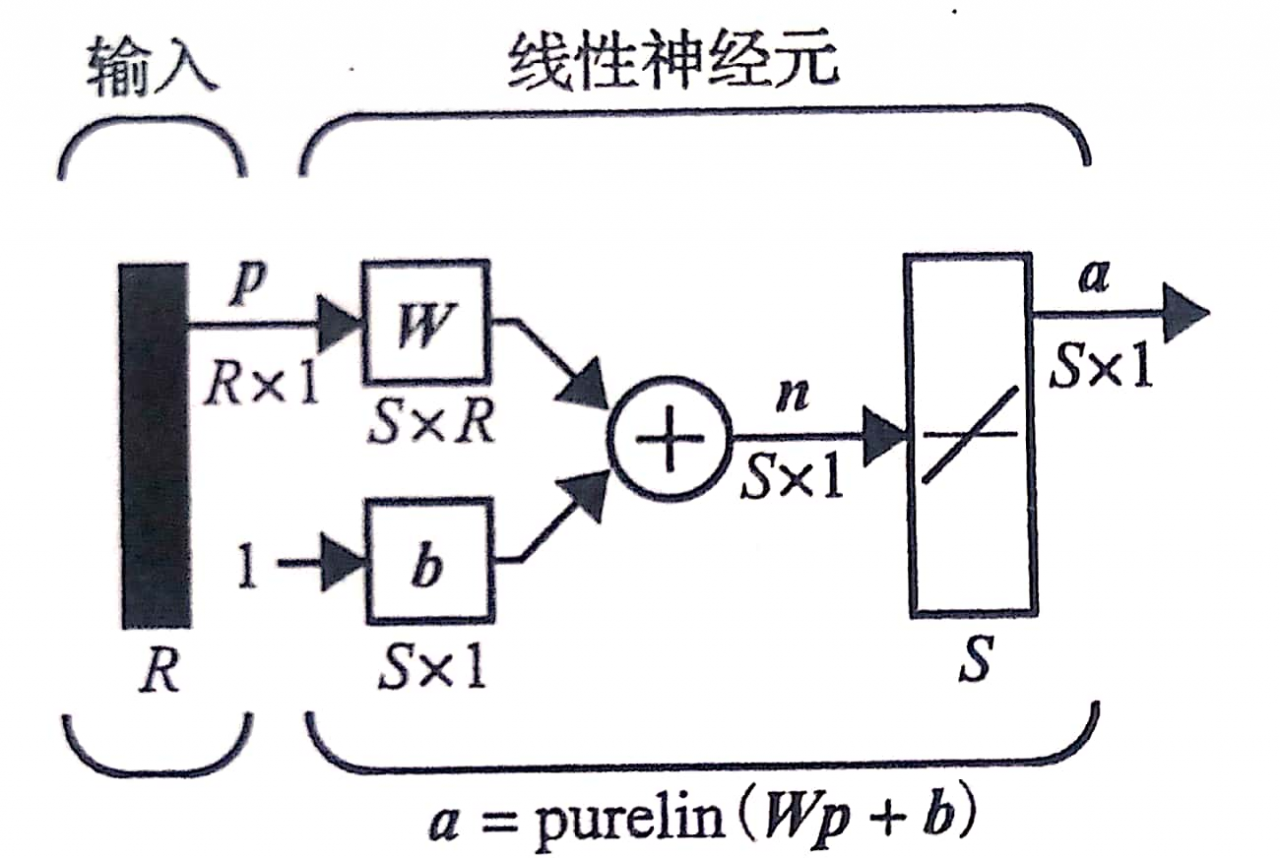
对于上图所示的单层线性网络,该线性网络的均方误差性能函数时二次的,即:
F ( x ) = c + d T x + 1 2 x T Ax F(x) = c + d^{T}x + \frac{1}{2}x^{T}\text{Ax}F(x)=c+dTx+21xTAx
其中,为Hessian矩阵。
① 为了研究提前终止法性能,我们将分析最速下降法在线性网络上的演化。由式10.16知性能指标的梯度:
∇ F ( x ) = A x + d \nabla F(x) = Ax + d∇F(x)=Ax+d
最速下降法:
x k + 1 = x k − α g k = x k − α ( A x k + d ) x_{k + 1} = x_{k} - \alpha g_{k} = x_{k} - \alpha(Ax_{k} + d)xk+1=xk−αgk=xk−α(Axk+d)
对于二次性能指标,极小值出现在下面的点:
x ML = − A − 1 d x^{\text{ML}} = - A^{- 1}dxML=−A−1d
上标ML表示结果使似然函数极大化同时使误差平方和极小化。则
x k + 1 = x k − α ( A x k + d ) = x k − α A ( x k + A − 1 d ) = x k − α A ( x k + x ML ) = [ I − αA ] x k + α A x ML = M x k + [ I − M ] A x ML {x_{k + 1} = x_{k} - \alpha(Ax_{k} + d)}\\{\text{}= x_{k} - \alpha A(x_{k} + A^{- 1}d)}\\{\text{} = x_{k} - \alpha A(x_{k} + x^{\text{ML}})}\\{\text{} = \left\lbrack I - \text{αA} \right\rbrack x_{k} + \alpha Ax^{\text{ML}}}\\{\text{} = Mx_{k} + \left\lbrack I - M \right\rbrack Ax^{\text{ML}}}xk+1=xk−α(Axk+d)=xk−αA(xk+A−1d)=xk−αA(xk+xML)=[I−αA]xk+αAxML=Mxk+[I−M]AxML
其中,M = ( I − α A ) M = (I - \alpha A)M=(I−αA)。
② 将x k + 1 x_{k + 1}xk+1与初始化权值x k x_{k}xk进行关联
x 1 = M x 0 + [ I − M ] x ML x_{1} = Mx_{0} + \left\lbrack I - M \right\rbrack x^{\text{ML}}x1=Mx0+[I−M]xML
x 2 = M x 1 + [ I − M ] x ML = M ( M x 0 + [ I − M ] x ML ) + [ I − M ] x ML = M 2 x 0 + [ I − M 2 ] x ML {x_{2} = Mx_{1} + \left\lbrack I - M \right\rbrack x^{\text{ML}}}\\{\text{} = M(Mx_{0} + \left\lbrack I - M \right\rbrack x^{\text{ML}}) + \left\lbrack I - M \right\rbrack x^{\text{ML}}}\\{\text{} = M^{2}x_{0} + \left\lbrack I - M^{2} \right\rbrack x^{\text{ML}}}x2=Mx1+[I−M]xML=M(Mx0+[I−M]xML)+[I−M]xML=M2x0+[I−M2]xML
递推可以得
KaTeX parse error: Undefined control sequence: \mspace at position 6: x_{k}\̲m̲s̲p̲a̲c̲e̲{6mu} = M^{k}x_…
贝叶斯正则化法分析
在误差平方和上加上一个惩罚项作为正则化性能指标,即:
F ( x ) = β E D + α E W F(x) = \beta E_{D} + \alpha E_{W}F(x)=βED+αEW
等价的性能指标:
F ∗ ( x ) = F ( x ) β = E D + α β E W = E D + ρ E W F^{*}(x) = \frac{F(x)}{\beta} = E_{D} + \frac{\alpha}{\beta}E_{W} = E_{D} + \rho E_{W}F∗(x)=βF(x)=ED+βαEW=ED+ρEW上式只有一个正则化参数。
权值平方和惩罚项E W E_{W}EW可以写为:
E W = ( x − x 0 ) T ( x − x 0 ) E_{W} = (x - x_{0})^{T}(x - x_{0})EW=(x−x0)T(x−x0)
其梯度为∇ E W = 2 ( x − x 0 ) \nabla E_{W} = 2(x - x_{0})∇EW=2(x−x0)
误差平方和的梯度:∇ E D = A x + d = A ( x + A − 1 d ) = A ( x − x ML ) \nabla E_{D} = Ax + d = A(x + A^{- 1}d) = A(x - x^{\text{ML}})∇ED=Ax+d=A(x+A−1d)=A(x−xML)
为了寻找正则化性能指标的极小值,同时也是最可能的值x MP x^{\text{MP}}xMP,令梯度为零。
∇ F ∗ ( x ) = ∇ E D + ρ ∇ E W = A ( x MP − x ML ) + 2 ρ ( x MP − x 0 ) = 0 \nabla F^{*}(x) = \nabla E_{D} + \rho\nabla E_{W} = A(x^{\text{MP}} - x^{\text{ML}}) + 2\rho(x^{\text{MP}} - x_{0}) = 0∇F∗(x)=∇ED+ρ∇EW=A(xMP−xML)+2ρ(xMP−x0)=0
化简:( A + 2 ρ I ) ( x MP − x ML ) = 2 ρ ( x 0 − x ML ) (A + 2\rho I)(x^{\text{MP}} - x^{\text{ML}}) = 2\rho(x_{0} - x^{\text{ML}})(A+2ρI)(xMP−xML)=2ρ(x0−xML)
求解x MP − x ML x^{\text{MP}} - x^{\text{ML}}xMP−xML,有
( x MP − x ML ) = 2 ρ ( A + 2 ρ I ) − 1 ( x 0 − x ML ) (x^{\text{MP}} - x^{\text{ML}}) = 2\rho(A + 2\rho I)^{- 1}(x_{0} - x^{\text{ML}})(xMP−xML)=2ρ(A+2ρI)−1(x0−xML)
移项:
x MP = 2 ρ ( A + 2 ρ I ) − 1 ( x 0 − x ML ) + x ML = M P ( x 0 − x ML ) + x ML \ n {x^{\text{MP}} = 2\rho(A + 2\rho I)^{- 1}(x_{0} - x^{\text{ML}}) + x^{\text{ML}}}\\{\text{} = M_{P}(x_{0} - x^{\text{ML}}) + x^{\text{ML}}\backslash n}xMP=2ρ(A+2ρI)−1(x0−xML)+xML=MP(x0−xML)+xML\n
其中,M P = 2 ρ ( A + 2 ρ I ) − 1 M_{P} = 2\rho(A + 2\rho I)^{- 1}MP=2ρ(A+2ρI)−1。
比较
提前终止法的结果表明从初始值到k次迭代后的最大似然权值我们进步了多少;
正则化法描述了正则化解与误差平方和极小值之间关系。

两个解等价↔ x k = x MP {\leftrightarrow x}_{k} = x^{\text{MP}}↔xk=xMP ↔ M k = M P {\leftrightarrow M}^{k} = M_{P}↔Mk=MP
M MM和A AA 具有相同的特征向量,A AA的特征值为λ i \lambda_{i}λi,M MM则的特征值为1 − α λ i 1 - \alpha\lambda_{i}1−αλi
,则M k M^{k}Mk的特征值为e i g ( M k ) = ( 1 − α λ i ) k eig(M^{k}) = (1 - \alpha\lambda_{i})^{k}eig(Mk)=(1−αλi)k
同理,可得M P M_{P}MP的特征值为e i g ( M P ) = 2 ρ λ i + 2 ρ eig(M_{P}) = \frac{2\rho}{\lambda_{i} + 2\rho}eig(MP)=λi+2ρ2ρ
因此,M k = M P M^{k} = M_{P}Mk=MP等价于
e i g ( M k ) = ( 1 − α λ i ) k = 2 ρ λ i + 2 ρ = e i g ( M P ) eig(M^{k}) = (1 - \alpha\lambda_{i})^{k} = \frac{2\rho}{\lambda_{i} + 2\rho} = eig(M_{P})eig(Mk)=(1−αλi)k=λi+2ρ2ρ=eig(MP)
取对数,有:
k log ( 1 − α λ i ) = − log ( 1 + λ i 2 ρ ) k\log(1 - \alpha\lambda_{i}) = - \log(1 + \frac{\lambda_{i}}{2\rho})klog(1−αλi)=−log(1+2ρλi)
为使上式成立,则λ i = 0 \lambda_{i} = 0λi=0。
对等式两边求导,有:
− 1 ( 1 + λ i 2 ρ ) 1 2 ρ = k 1 − α λ i ( − α ) - \frac{1}{(1 + \frac{\lambda_{i}}{2\rho})}\frac{1}{2\rho} = \frac{k}{1 - \alpha\lambda_{i}}( - \alpha)−(1+2ρλi)12ρ1=1−αλik(−α)
当α λ i \alpha\lambda_{i}αλi很小(缓慢、稳定的学习)且λ i 2 ρ \frac{\lambda_{i}}{2\rho}2ρλi很小,则有近似结果:
αk ≅ 1 2 ρ \text{αk} \cong \frac{1}{2\rho}αk≅2ρ1
因此,提前终止法和正则化法近似相等。增加迭代次数k kk近似于减少正则化参数ρ \rhoρ。可以直观看出,增加迭代次数或者减少正则化参数都能够引起过拟合。
参考资料
1.尹恩·古德费洛.深度学习[M].北京:人民邮电出版社,2017.8
2.马丁 T·哈根,章毅(译).神经网络设计[M].北京:机械出版社,2017.12