什么是矩阵?
按照课本上的定义:
矩阵就是由m行n列数放在一起组成的数学对象。
或者更简单一点:
把数列排成矩形,就是矩阵。
对于一个n行m列的矩阵,我们把它叫做一个n×m矩阵。当矩阵的行数和列数相同时,我们称这样的矩阵为正方矩阵,根据其规模将其称为2阶矩阵、3阶矩阵等。通常,用大写字母表示矩阵,用小写字母表示矩阵内的元素。
矩阵的运算-加法和数乘
矩阵的加法和数量乘法的方法和向量基本上是一样的,如下所示(来源:《程序员的数学3 线性代数》)。
下面,我们引入非常重要的运算方法:矩阵与向量的乘积。
其实,矩阵与向量的乘积,可以想成是把向量“放平”,然后分别于矩阵中每一行对应的元素相乘并求和。但是在计算过程中需要注意以下几点:
- 矩阵与向量的乘积是向量
- 矩阵与向量相乘时,矩阵的列数与向量的维数要相等
对矩阵的进一步理解——映射
矩阵和向量的乘积,其实表示了一种“平直”的关系,也就是说,各个数据之间是不相互影响的,只是单纯的各种因素的加和。在这里,我们先说一下“线性映射”的概念。
一般来说,满足 f(x+y)=f(x)+f(y) 以及 f(cx)=cf(x) 的映射f,我们称其为线性映射(其中,x, y 为维数相同的向量,c为常数)。
我们可以看到,将n维向量 x 乘以m×n矩阵 A ,得到的结果是一个m维向量(即f(x)),仍然满足矩阵的加法和数乘规律,也就是说,通过矩阵A,我们确定了一个向量到另一个向量的映射,所以说“矩阵就是用坐标来表示的线性映射”。下图可以直观的表示这种映射关系(来源:《程序员的数学3 线性代数》):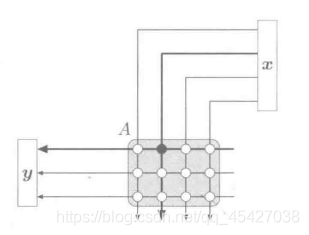
因为向量可以作为一个点的“位置坐标”,你们在这个理解之上,我们可以说,矩阵,描述了一个“点”到另一个"点"的移动(当然,向量可以是很高维的,大多时候并不是代表一个点)。那么,更广泛一点来说,m×n矩阵 A ,实际上表示的是从 n 维空间到 m 维空间的映射。
在我惊讶于“从 n 维空间到 m 维空间的映射”这句话的时候,我又发现了另一个很有趣味的解释——“矩阵是线性空间里的变换的描述”,在这里和大家一起分享一下:
向量:向量描述对象(在选定基之后)
矩阵:矩阵描述对象的运动(在选定基之后)
是某个对象发生要求的运动,就是用描述此运动的矩阵乘以代表该对象的向量:运动×对象=矩阵×向量
矩阵的乘积
在理解了矩阵和向量的乘积之后,我们来看矩阵和矩阵的乘积(来源:《程序员的数学3 线性代数》):
如果没有看懂的话,可以看这个: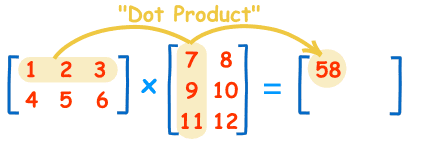
其实,就相当于把后一个矩阵拆成 n 个向量,分别求积再组合(我自己想的,可能不大严谨)。注意,在矩阵相乘的时候,一定要保证 B 的宽度(列数)和 A 的高度(行数)相等。
我们刚刚说,矩阵是映射,那矩阵与矩阵的乘积是什么意思呢?其实,我们可以简单的将其理解为“映射的合成”,将右边矩阵按列分割开来看做若干个列向量,通过左边矩阵的“映射”转换后再组合成为一个新的矩阵,具体的意义之后结合具体的矩阵变换具体分析吧,OK,Bye~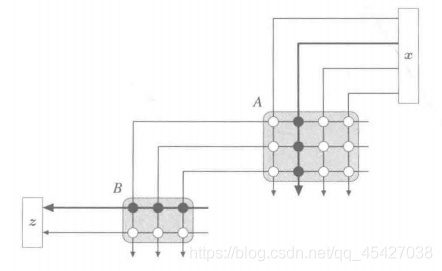
参考:
https://www.cnblogs.com/fengff/p/9758272.html
https://blog.csdn.net/u012513525/article/details/78077151(强烈推荐)
《程序员的数学3 线性代数》(强烈推荐)
https://blog.csdn.net/c991262331/article/details/79893108