归并排序

基本思想：利用归并的思想实现的排序算法，该算法采用经典的分治策略。分治法分为两个阶段，首先是分阶段，分阶段将问题分成一系列小的问题然后进行递归求解，然后是治阶段，治阶段将分阶段得到的各个答案“修补”在一起，这就是分而治之。

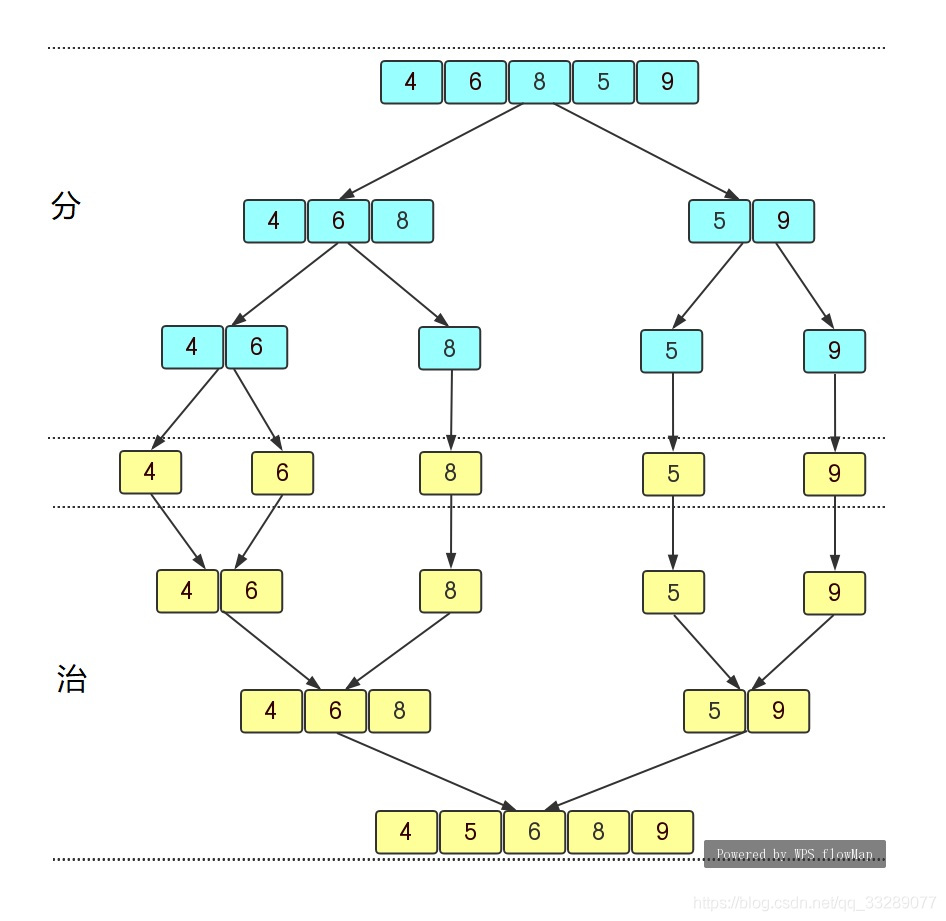
算法实现：对于一个无序序列{4，6，8，5，9}我们使用分治策略可以画出如下图所示，可以看出这种结构很像一颗树，所以我们可以使用递归的方式去实现，分阶段是递归拆分子序列的过程，而治阶段则是将两个已经有序的子序列合并成一个有序的序列。

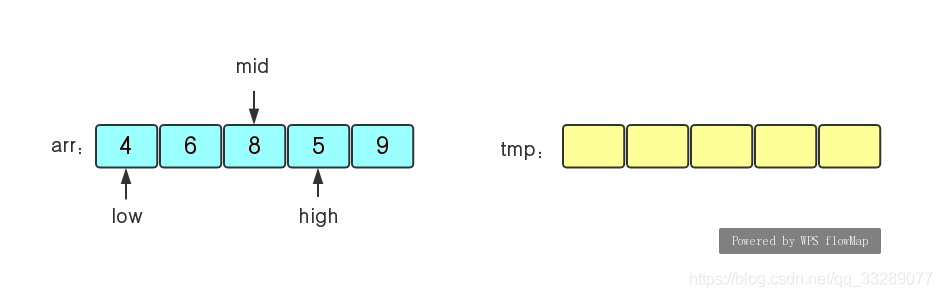
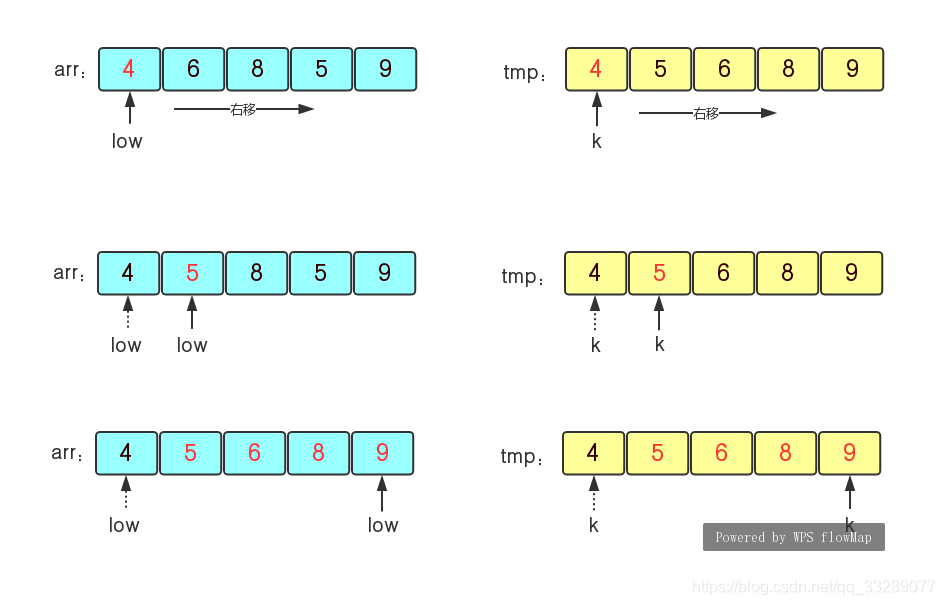
步骤（1）对于无序序列arr{4，6，8，5，9}来说，我们初始化时让low为序列的首元素下标，mid=low+arr.length，high=mid+1，tmp为辅助序列。

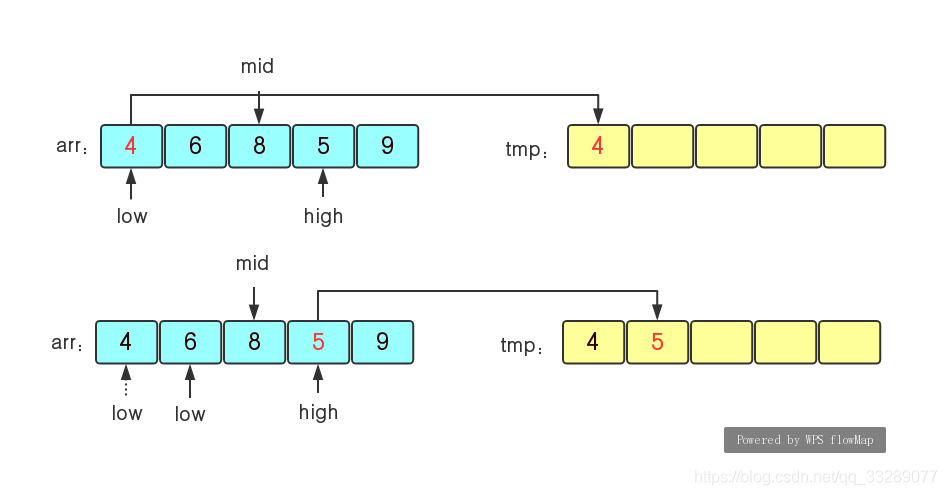
步骤（2）比较low和high所指的元素，谁小谁就插入到tmp序列中，然后谁再向右走一个单位。如下图所示，4<5，将4插入到tmp中，然后low向右走一个单位，然后5<6，再将5插入tmp中，high向右走一个单位。

步骤（3）接着继续（2）步骤，一直到将无序序列中的元素全部插入到tmp中为止，这样tmp就是一个有序的序列了。

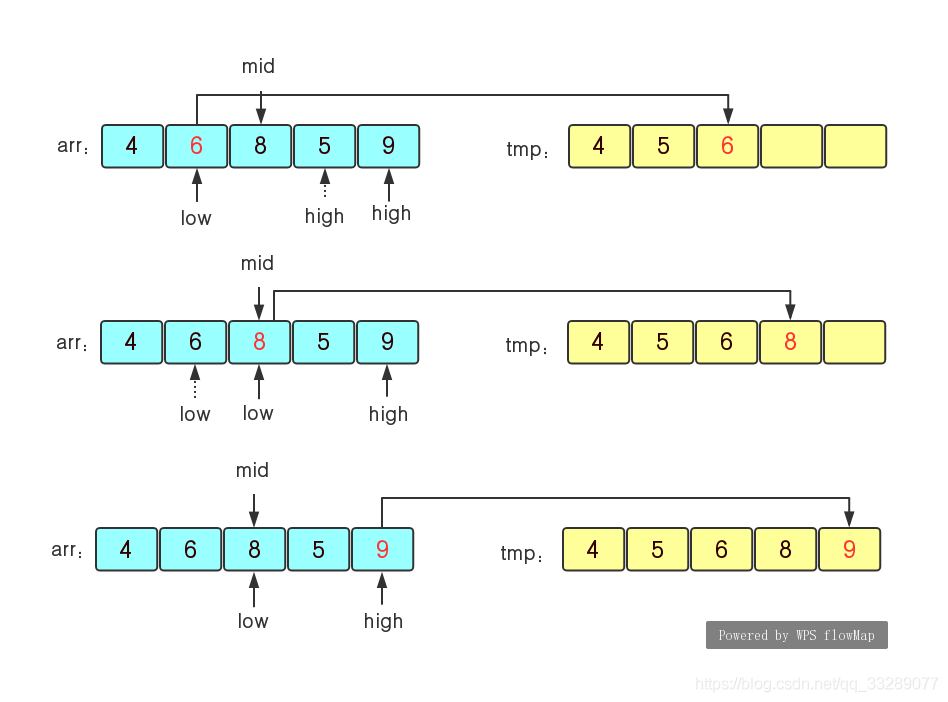
步骤（4）在得到无序序列tmp后我们将tmp中的数据拷贝到原序列arr中，这样就将原序列arr变成了一个有序序列。

代码实现：

//归并排序（递归）
void Merge(int *arr,int low,int mid,int high,int *tmp)
{
	int i = low;
	int j = mid + 1;
	int k = 0;
	while (i <= mid && j <= high)
	{
		if (arr[i] <= arr[j])
		{
			tmp[k++] = arr[i++];
		}
		else
		{
			tmp[k++] = arr[j++];
		}
	}
        //将剩下的有序的数据存入tmp数组中
	while (i <= mid)
	{
		tmp[k++] = arr[i++];
	}
	while (j <= high)
	{
		tmp[k++] = arr[j++];
	}
        //将tmp数组中的元素拷贝到原数组中
	k = 0;
	while (low <= high)
	{
		arr[low++] = tmp[k++];
	}
}
void MergeSort1(int *arr,int low,int high,int *tmp)
{
	if (low < high)
	{
		int mid = (low + high) / 2;
		MergeSort1(arr,low,mid,tmp);
		MergeSort1(arr,mid+1,high,tmp);
		Merge(arr,low,mid,high,tmp);
	}
}
//归并排序（非递归）
void MergeSort_pass(int *arr,int len,int k,int*tmp)
{
	int i = 0;
	while (i < len - 2 * k + 1)
	{
		Merge(arr,i,i+k-1,i+2*k-1,tmp);
		i = i + 2 * k;
	}
	if (i < len - k + 1)
	{
		Merge(arr,i,i+k-1,len-1,tmp);
	}
}

void MergeSort2(int *arr, int len, int *tmp)
{
	int k = 1;
	while (k <= len)
	{
		MergeSort_pass(arr,len,k,tmp);
		k = k * 2;
	}
}