一元线性回归系数的推导
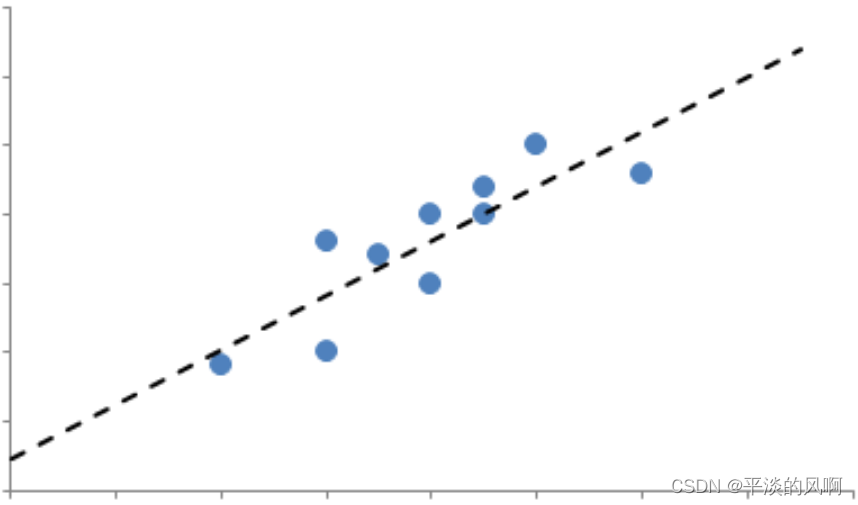
假设有n个离散的点( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x n , y n ) {(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}(x1,y1),(x2,y2),⋯,(xn,yn),我们要拟合一条直线y = m x + b y=mx+by=mx+b来寻找x xx和y yy的关系。
我们通过最小化平方误差来求拟合直线的系数m mm和b bb。
最小化平方误差squared error
S E L I N E = ∑ i = 1 n ( y i − ( m x i + b ) ) 2 = ∑ i = 1 n y i 2 − 2 m ∑ i = 1 n x i y i − 2 b ∑ i = 1 n y i + 2 m b ∑ i = 1 n x i + m 2 ∑ i = 1 n x i 2 + n b 2 = n y 2 ‾ − 2 m n x y ‾ − 2 b n y ‾ + 2 m b n x ‾ + m 2 n x 2 ‾ + n b 2 \begin{aligned} SE_{LINE}&=\sum_{i=1}^{n}(y_i-(mx_i+b))^2\\ &=\sum_{i=1}^{n}y_i^2-2m\sum_{i=1}^{n}x_iy_i-2b\sum_{i=1}^{n}y_i+2mb\sum_{i=1}^{n}x_i+m^2\sum_{i=1}^{n}x_i^2+nb^2\\ &=n\overline{y^2}-2mn\overline{xy}-2bn\overline{y}+2mbn\overline{x}+m^2n\overline{x^2}+nb^2 \end{aligned}SELINE=i=1∑n(yi−(mxi+b))2=i=1∑nyi2−2mi=1∑nxiyi−2bi=1∑nyi+2mbi=1∑nxi+m2i=1∑nxi2+nb2=ny2−2mnxy−2bny+2mbnx+m2nx2+nb2
分别对m mm和b bb求偏导可得
{ m x 2 ‾ + b x ‾ = x y ‾ m x ‾ + b = y ‾ \begin{cases} m\overline{x^2}+b\overline{x}=\overline{x y} \\ m\overline{x}+b=\overline{y} \end{cases}{mx2+bx=xymx+b=y
从而有m = x y ‾ − x ‾ y ‾ x 2 ‾ − x ‾ 2 = C o v ( X , Y ) V a r ( X ) m=\frac{\overline{xy}-\overline{x}\overline{y}}{\overline{x^2}-\overline{x}^2}=\frac{Cov(X,Y)}{Var(X)}m=x2−x2xy−xy=Var(X)Cov(X,Y)
即可得到回归系数。