t-SNE算法

t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法，是由 Laurens van der Maaten 和 Geoffrey Hinton在 08 年提出来。t-SNE 是一种非线性降维算法，非常适用于高维数据降维到 2 维或者 3 维，进行可视化。在实际应用中，t-SNE很少用于降维，主要用于可视化，可能的原因有以下几方面：

• 当我们发现数据需要降维时，一般是特征间存在高度的线性相关性，此时我们一般使用线性降维算法，比如PCA。即使是特征之间存在非线性相关，也不会先使用非线性降维算法降维之后再搭配一个线性的模型，而是直接使用非线性模型；
• 一般 t-SNE 都将数据降到 2 维或者 3 维进行可视化，但是数据降维降的维度一般会大一些，比如需要降到 20 维，t-SNE 算法使用自由度为 1 的 t 分布很难做到好的效果，而关于如何选择自由度的问题，目前没有研究；
• t-SNE 算法的计算复杂度很高，另外它的目标函数非凸，可能会得到局部最优解；

在可视化的应用中，t-SNE的效果要好于 PCA，下面是对手写数字可视化的一个结果对比，上面的图是 PCA 降维到2维的结果，下面是 t-SNE算法的结果。对可视化的效果衡量，无非是两方面：相似的数据是不是离得近，不相似的数据是不是离得远。从这两方面来讲，t-SNE的效果要明显优于 PCA。

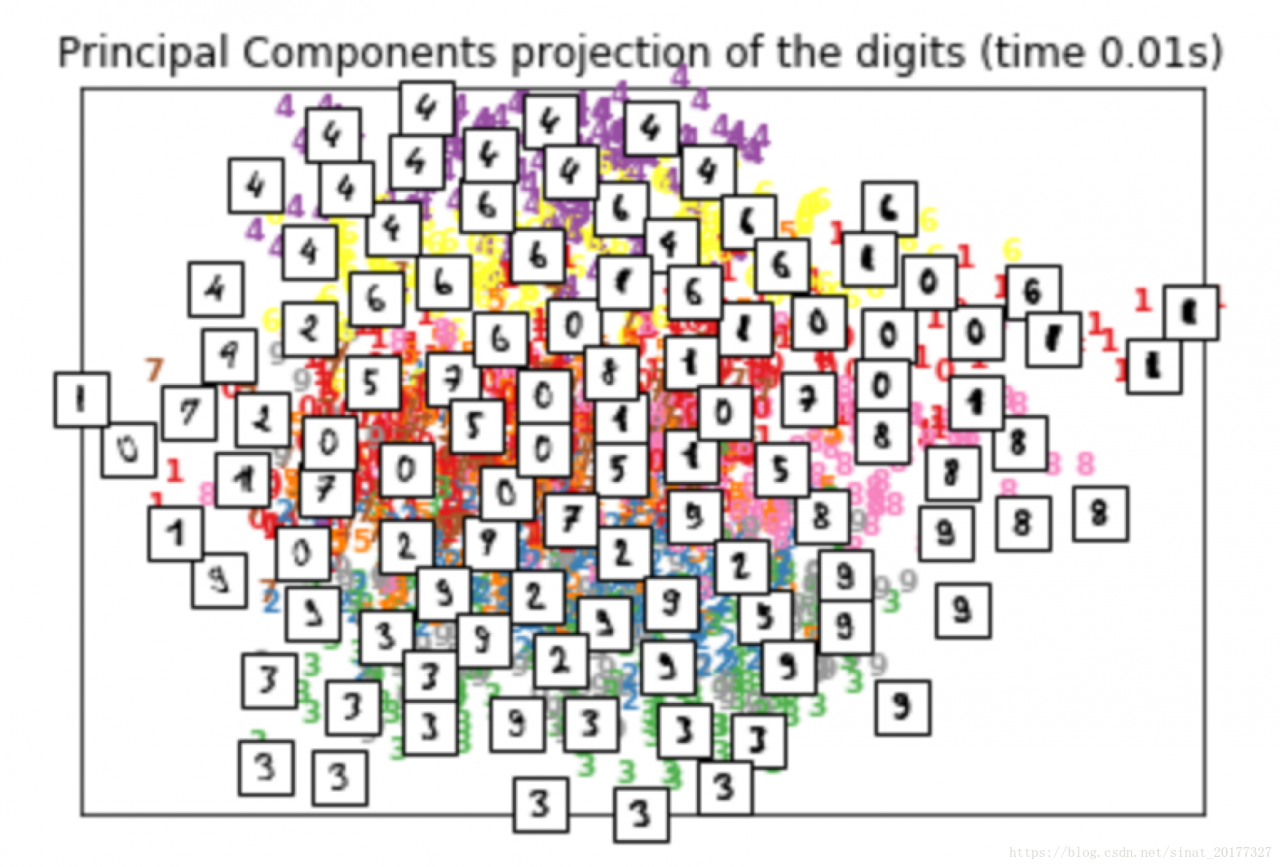
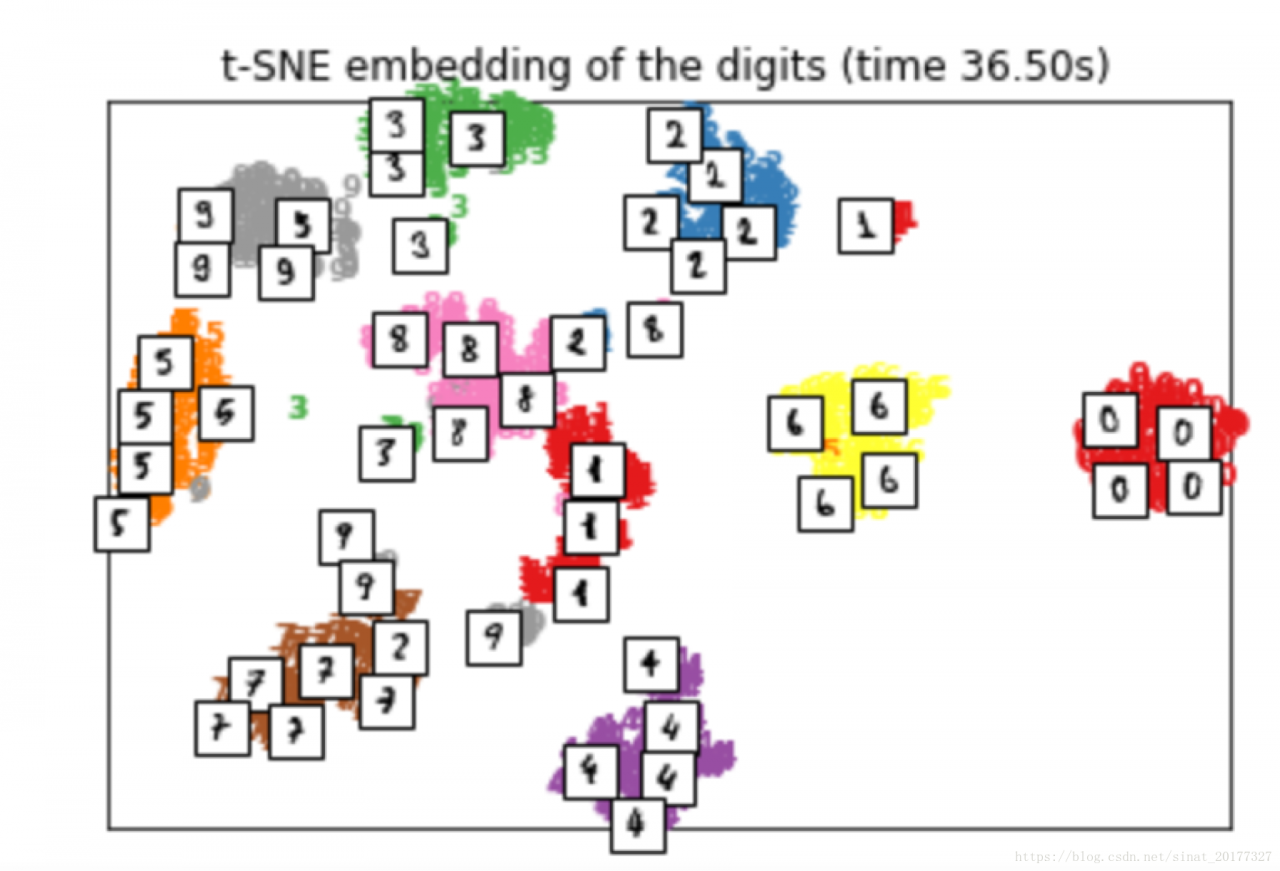
一、SNE

1、基本思想

t-SNE算法由 SNE 改进而来，所以先来介绍 SNE。给定 n 个高维数据 ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$，若将其降维至 2 维，SNE 的基本思想是若两个数据在高维空间中是相似的，那么降维至 2 维空间时它们应该离得很近。

2、相似性计算

SNE使用条件概率来描述两个数据之间的相似性，假设${{x}_{i}},{{x}_{j}}$是高维空间中的两个点，那么以点${{x}_{i}}$为中心构建方差为${{\sigma }_{i}}$的高斯分布，使用 ${{p}_{j|i}}$表示${{x}_{j}}$是${{x}_{i}}$邻域的概率，如果${{x}_{j}}$离${{x}_{i}}$很近，那么${{p}_{j|i}}$很大，反之，${{p}_{j|i}}$很小，${{p}_{j|i}}$定义如下：

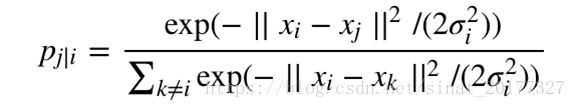
我们只关心不同点对之间的相似度，所以设定 ${{p}_{i|i} = 0}$。

那么在低维空间中也可以使用这样的条件概率来定义距离，假设 ${{x}_{i}},{{x}_{j}}$映射到低维空间后对应 ${{y}_{i}},{{y}_{j}}$，${{y}_{j}}$是 ${{y}_{i}}$邻域的条件概率为 ${{q}_{j|i}}$：

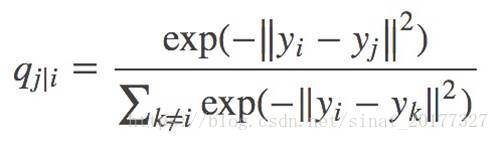
低维空间中的方差直接设置为 ${{\sigma }_{i}}=\sqrt{2}/1$，方便计算，同样 ${{q}_{i|i} = 0}$。

3、目标函数

在高维空间中，如果考虑 ${{x}_{i}}$与其他所有点之间的条件概率，那么会构成一个条件概率分布 ${{P}_{i}}$，同样在地位空间也会有与之对应的条件概率分布 ${{Q}_{i}}$，如果降维之后的数据分布与原始高维空间中的数据分布是一样的，那么理论上这两个条件概率分布式是一致的。那么如何衡量两个条件概率分布之间的差异呢？答案是使用 K-L 散度（也叫做相对熵），于是，目标函数为：

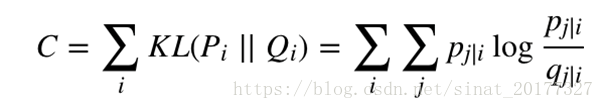
分析：

• 当 ${{p}_{j|i}}$= 0.9，也就是 ${{x}_{j}}$离${{x}_{i}}$很近时，如果算法计算映射到低维空间的 ${{p}_{j|i}}$= 0.1，也就是映射后 ${{x}_{j}}$离${{x}_{i}}$很远，那么此时目标函数会有一个很大的损失。SNE算法也因此保证了数据的局部性；
• 当 ${{p}_{j|i}}$= 0.1，也就是 ${{x}_{j}}$离${{x}_{i}}$很远时，如果算法计算映射到低维空间的 ${{p}_{j|i}}$= 0.9，也就是映射后 ${{x}_{j}}$离${{x}_{i}}$很近，那么此时目标函数会有一个很小的损失，实际上我们并不希望得到这样的结果，一个大的损失才是我们想要的，但由于 K- L 散度本身的不对称性，这一缺陷无法避免，后续我们看 t-SNE 算法如何对其进行改进。

4、SNE缺点

通过以上的介绍，总结一下SNE的缺点：

• 不对称导致梯度计算复杂，对目标函数计算梯度如下，由于条件概率 ${{p}_{j|i}}$不等于 ${{p}_{i|j}}$，${{q}_{j|i}}$不等于 ${{q}_{i|j}}$，因此梯度计算中需要的计算量较大。

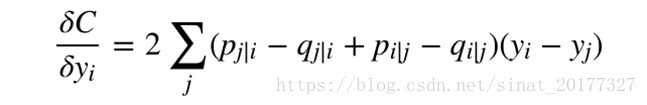
• 拥挤问题。所谓拥挤问题，顾名思义，就是不同类别的簇挤在一起，无法区分开来，这就是拥挤问题。有的同学说，是不是因为SNE更关注局部结构，而忽略了全局结构造成的？实际上，拥挤问题的出现与某个特定算法无关，而是由于高维空间距离分布和低维空间距离分布的差异造成的。

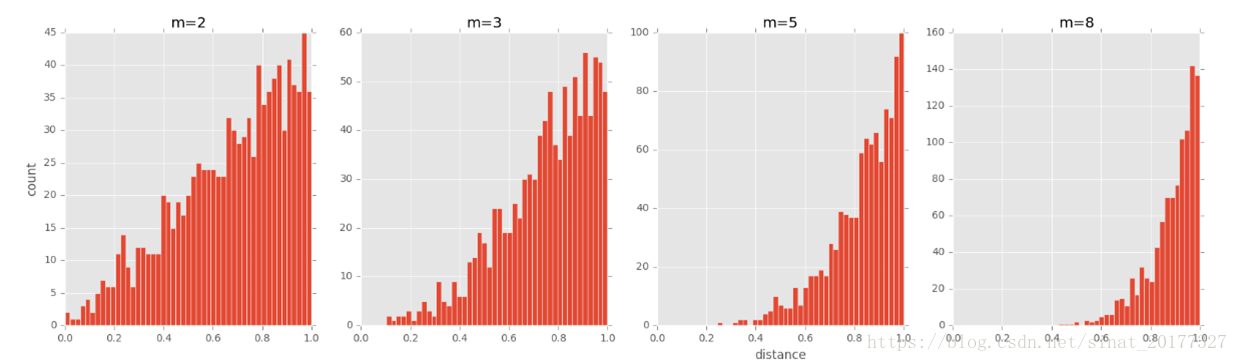
假设一个以数据点 ${{x}_{i}}$为中心，半径为 r 的 m 维球(二维空间就是圆，三维空间就是球)，其体积是按 r 的 m 次方增长的，假设数据点是在 m 维球中均匀分布的，我们来看看其他数据点与 ${{x}_{i}}$的距离随维度增大而产生的变化。从图中可以看到，随着维度的增大，大部分数据点都聚集在 m 维球的表面附近，与点 ${{x}_{i}}$的距离分布极不均衡。如果直接将这种距离关系保留到低维，肯定会出现拥挤问题。

• 由于K - L散度本身的不对称性，使得SNE算法只关注数据局部性而忽略了数据的全局性。

针对以上 3 个缺点，在 t-SNE 中会如何改进呢？

二、t-SNE

1、对称SNE

原始 SNE 中，在高维空间中条件概率 ${{p}_{j|i}}$不等于 ${{p}_{i|j}}$，低维空间中 ${{q}_{j|i}}$不等于 ${{q}_{i|j}}$，于是提出对称 SNE，采用更加通用的联合概率分布代替原始的条件概率，使得 ${{p}_{ij}}$= ${{p}_{ji}}$，${{q}_{ij}}$= ${{q}_{ji}}$

简单来讲，在低维空间中定义 ${{q}_{ij}}$：

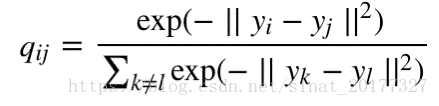
当然，在高维空间我们也可以定义 ${{p}_{ij}}$：

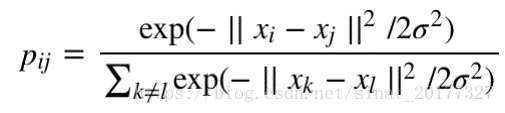
但是在高维空间中这样的定义会带来异常值的问题，怎么理解呢？假设点 ${{x}_{i}}$是一个噪声点，那么 || ${{x}_{i}}$- ${{x}_{j}}$|| 的平方会很大，那么对于所有的 j，${{p}_{ij}}$的值都会很小，导致在低维映射下的 ${{y}_{i}}$对整个损失函数的影响很小，但对于异常值，我们显然需要得到一个更大的惩罚，于是对高维空间中的联合概率修正为：

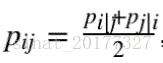
这样就避免了异常值的问题，此时的梯度变为：

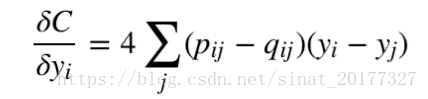
相比于原始 SNE，对称 SNE 的梯度更加简化，计算效率更高。但对称SNE的效果只是略微优于原始SNE的效果。

2、引入 t 分布

我们回到刚才 SNE 存在的两个缺点的第二个，拥挤问题，这个问题的解决在 t-SNE 中就是使用 t 分布。t 分布是一种长尾分布，从图中可以看到，在没有异常点时，t 分布与高斯分布的拟合结果基本一致。而在第二张图中，出现了部分异常点，由于高斯分布的尾部较低，对异常点比较敏感，为了照顾这些异常点，高斯分布的拟合结果偏离了大多数样本所在位置，方差也较大。相比之下，t 分布的尾部较高，对异常点不敏感，保证了其鲁棒性，因此其拟合结果更为合理，较好的捕获了数据的整体特征。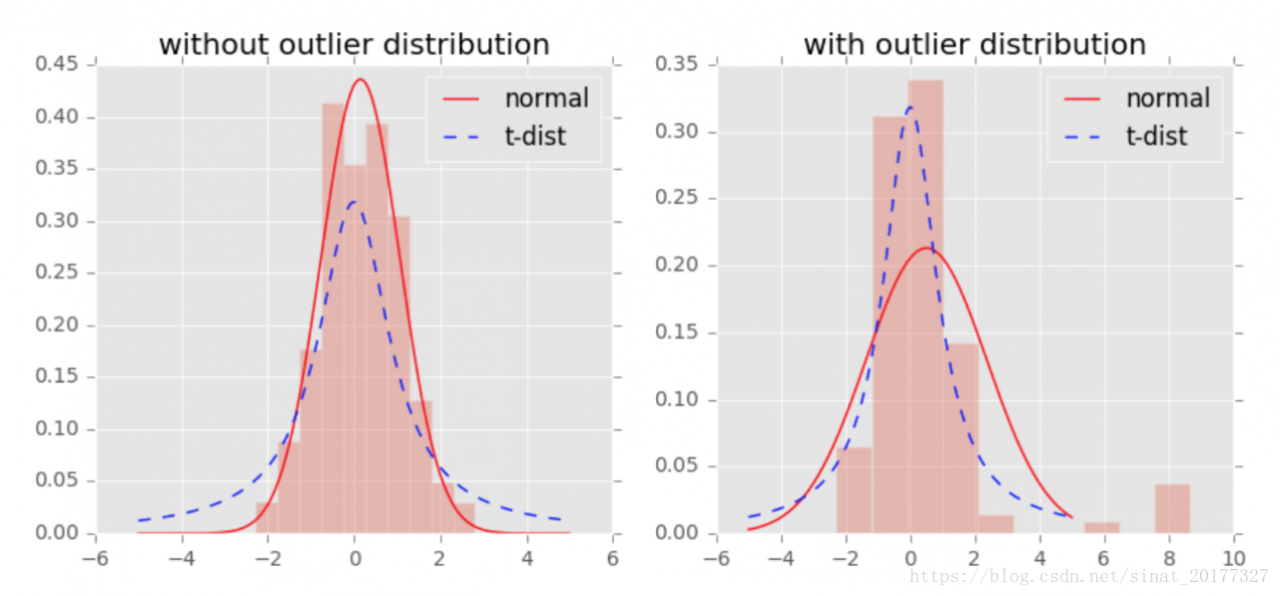

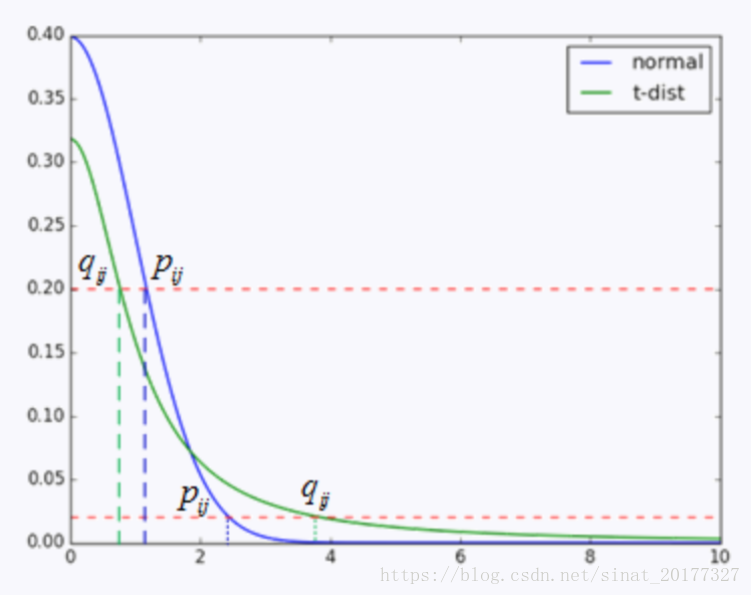
那么如何利用 t 分布的长尾性来改进 SNE 呢？我们来看下面这张图，注意这个图并不准确，主要是为了说明 t 分布是如何发挥作用的。

图中有高斯分布和 t 分布两条曲线，表示点之间的相似性与距离的关系，高斯分布对应高维空间，t 分布对应低维空间。那么对于高维空间中相距较近的点，为了满足 ${{p}_{ij}}$= ${{q}_{ij}}$，低维空间中的距离需要稍小一点；而对于高维空间中相距较远的点，为了满足 ${{p}_{ij}}$= ${{q}_{ij}}$，低维空间中的距离需要更远。这恰好满足了我们的需求，即同一簇内的点(距离较近)聚合的更紧密，不同簇之间的点(距离较远)更加疏远。

引入 t 分布之后，在低维空间中，用自由度为1的t分布重新定义 ：

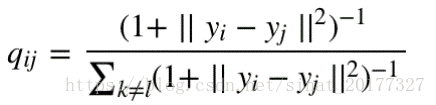
然后与原始 SNE 一样，我们使用 K-L 散度定义目标函数进行优化，从而求解。至此，关于 t-SNE 算法的原理部分，我们就介绍完了。

3、总结

总结一下 t-SNE 算法的改进：

• 把SNE变为对称SNE，提高了计算效率，效果稍有提升
• 在低维空间中采用了t分布代替原来的高斯分布，解决了拥挤问题，优化了SNE过于关注局部特征忽略全局特征的问题
  下面是 SNE 算法和 T-SNE 算法的可视化结果对比，可以看到， T-SNE 算法的效果要远远好于 SNE。

SNE：

T-SNE：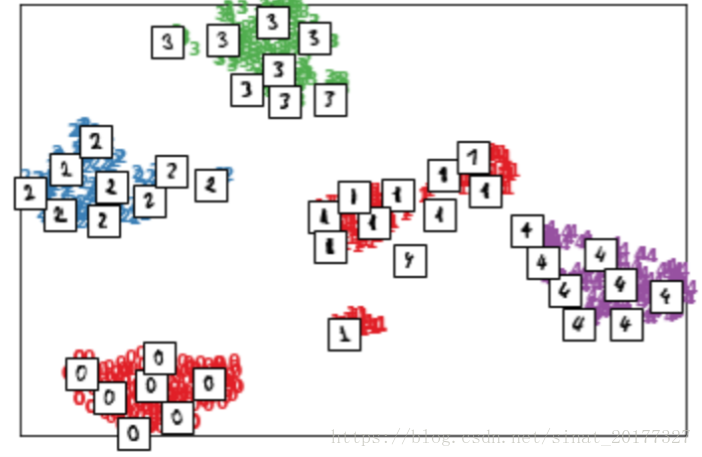

总结一下 t-SNE 算法的不足：

• 主要用于可视化，很难用于其他目的.比如降维到10维，因为t分布偏重长尾，1个自由度的 t 分布很难保存好局部特征，可能需要设置成更高的自由度；
• t-SNE 没有唯一最优解，且不能用于预测，比如测试集合降维，因为他没有显式的预估部分，不能在测试集合直接降维；
• 速度慢