一、建堆
1.堆的概念及性质
如果有一个关键码的集合 K = {k0 , k1 , k2 , … , kn-1} ,把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2 i+1 且 Ki<= K2 i+2 (Ki >= K2 i+1 且 Ki >= K2 i+2) i = 0 , 1 , 2… ,则称为小堆( 或大堆 ) 。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:堆中某个节点的值总是不大于或不小于其父节点的值;堆总是一棵完全二叉树。
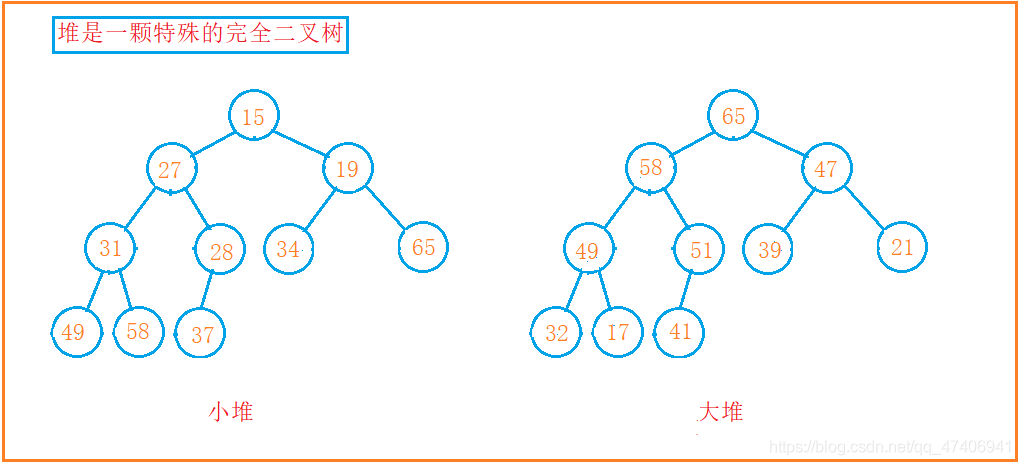
堆的特点:大堆的根节点最大小堆的跟节点最小;堆是一颗特殊的完全二叉树。
2.堆的构建
①向下调整算法
算法作用:将一个根节点的左右孩子均为大堆(小堆)的完全二叉树(非堆)堆调整成大堆(小堆)。
前提条件:对于大堆,根节点的左右孩子都必须是一个大堆;对于小堆,根节点的左右孩子都必须是小堆。
算法思路:根节点和较小(较大)的孩子进行比较,如果根节点小于(大于)孩子节点,则交换位置,如此迭代。
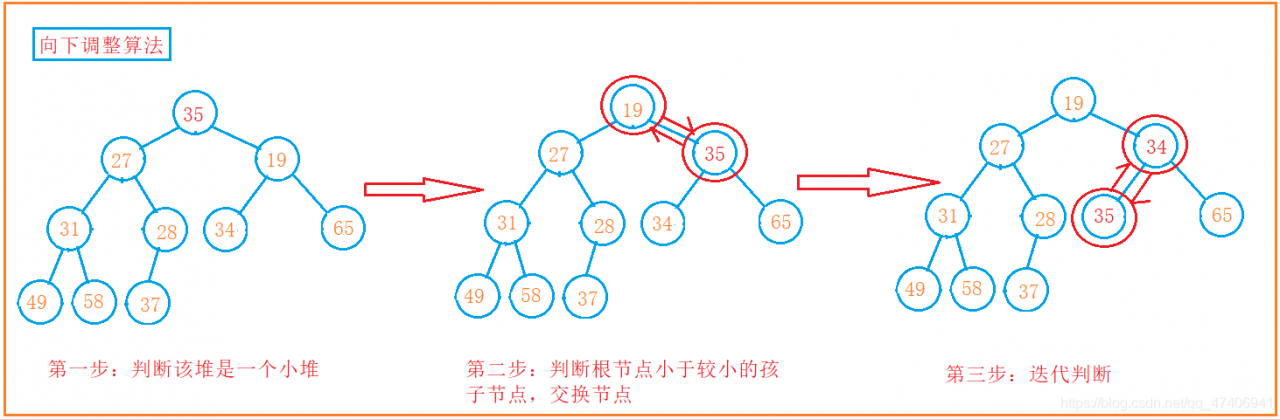
代码实现:

//向下调整算法(小堆)
void AdjustDown(int* heap, int root,int n)
{
int parent = root;
int child = parent * 2 + 1;
//当父节点不在有子节点终止迭代(子节点超出数组下标)
while (child+1 < n && child < n)
{
//选出较小的子节点
if (child > n && heap[child] > heap[child + 1])
{
child = child + 1;
}
//比较父子节点大小关系
if (heap[parent] > heap[child])
{
//交换父子节点
int temp = heap[parent];
heap[parent] = heap[child];
heap[child] = temp;
}
else
{
//如果父节点小于子节点,提前退出程序,终止迭代
break;
}
parent = child;
child = parent * 2 + 1;
}
}②向上调整算法
作用:向堆中插入一个数据可以使用向上调整算法实现。
在向堆中插入一个数据时,如果将要插入的数据放在数组下标为0的位置利用向下调整算法进行调整,则需要将数组整体后移,当堆较大时这样做就会有较大的性能损耗。使用向上调整算法的思路是将要插入的数据放在数组尾部,进行向上调整。
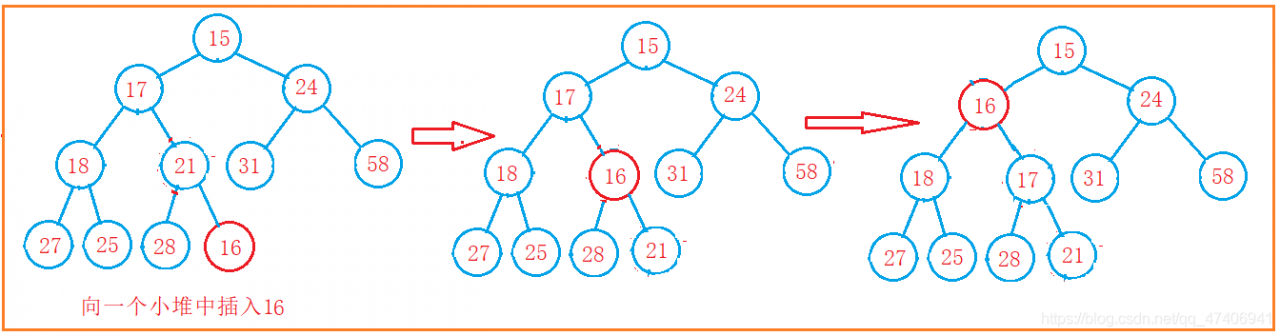
代码描述:
//向上调整算法
void AdjustUp(int* heap, int child, int n)
{
//找到叶子节点的父节点
int parent = (child - 1) / 2;
while (child > 0)
{
//判断叶子节点是否小于父节点,小于就进行替换
if (heap[child] < heap[parent])
{
int temp = heap[child];
heap[child] = heap[parent];
heap[parent] = temp;
}
else
{
break;
}
child = parent;
parent = (child-1)/2;
}
}③构建堆
思路:从第一个非叶子结点开始向上迭代,利用向下调整算法创建。
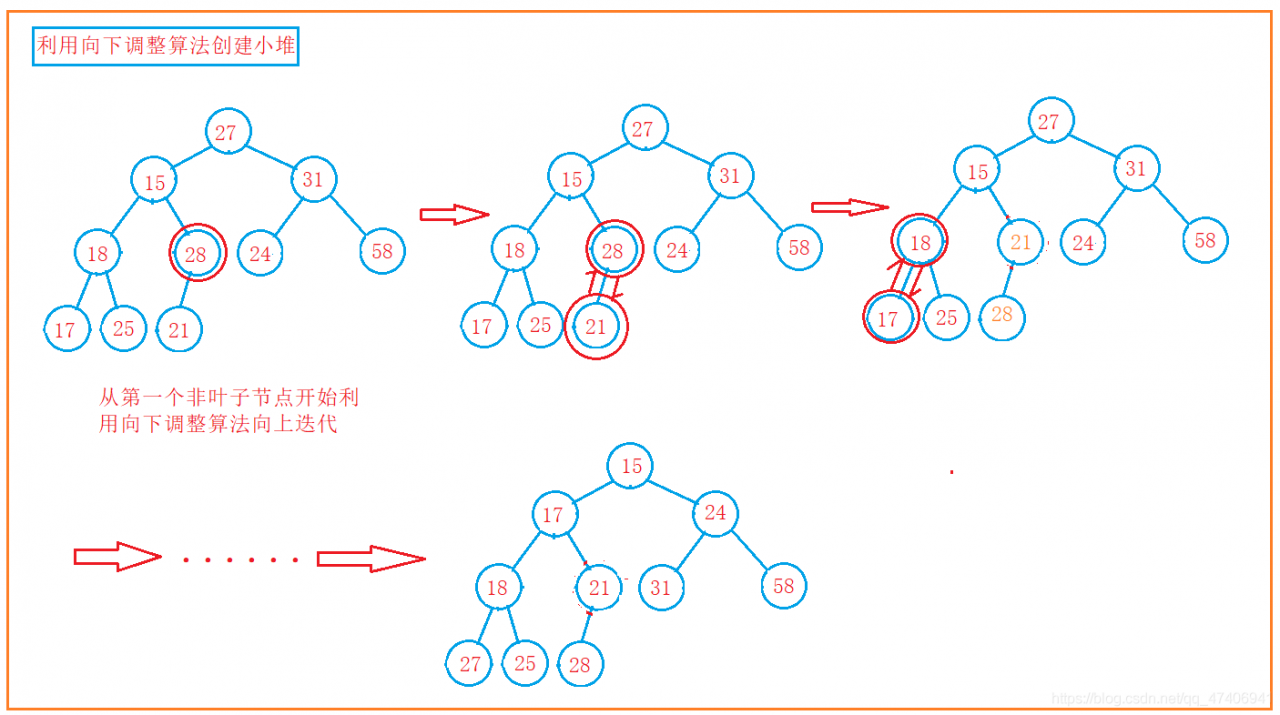
最后一个非叶子节点的计算:假设一共有n个节点,最后一个节点的小标为n-1,最后一个非叶子节点就是最后一个节点的父节点,因此,最后一个非叶子节点的下标为:(n-2)/2;
代码描述:
//利用向下调整算法创建堆(小堆)
void HeapCreate(int* heap,int root,int n)
{
//利用向下调整算法,从第一个非叶子结点开始调整。
int i = (n - 2) / 2;
for (; i >= root; i--)
{
AdjustDown(heap,i,n);
}
}二、堆排序
算法思路:利用堆的特点(根节点为最大(最小))每次将堆的根节点跟最后一个叶子节点进行交换,在对堆进行向下调整。
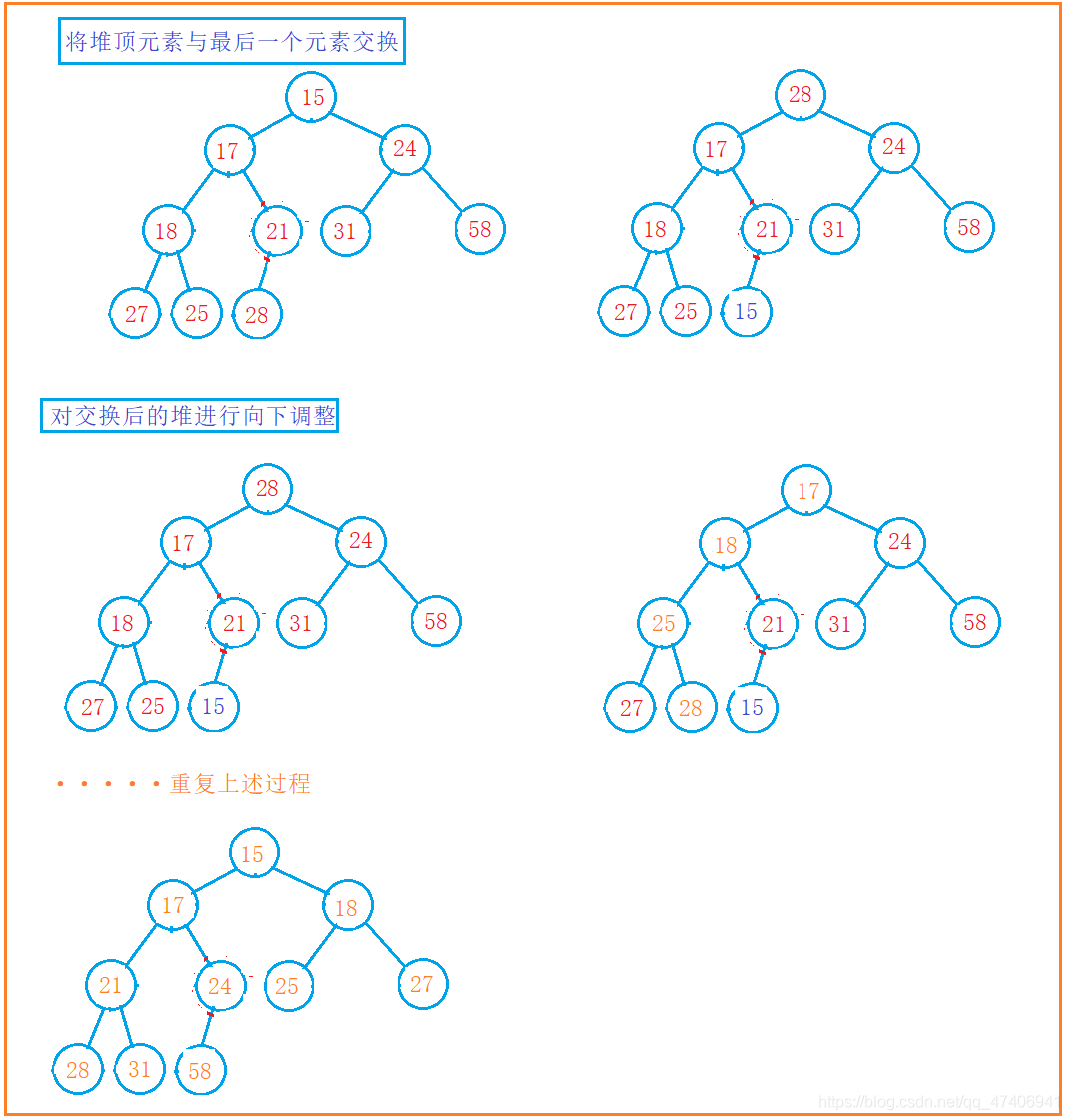
时间复杂度:O(N*logN)
特点:升序排序建大堆,降序排序建小堆。
算法描述:
//堆排序
void HeapSort(int* heap, int n)
{
int m = n;
int i = 1;
//迭代n-1次
for (i = 1; i < n; i++)
{
//交换堆根元素和最后一个叶子节点
int temp = heap[m - 1];
heap[m - 1] = heap[0];
heap[0] = temp;
//新堆大小减1
m--;
//对堆进行向下调整(最后一个叶子节点不进行调整)
AdjustDown(heap, 0, m);
}
}
版权声明:本文为qq_47406941原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。