数据摘要
反映集中程度的函数
下面是R中反映中程度的函数
- mean():均值
- median():中位数
- quantile():分位数
> a <- c(1,5,6,9,7,5,6,7,2,6)
> mean(a)
[1] 5.4
> median(a)
[1] 6
> quantile(a)
0% 25% 50% 75% 100%
1.00 5.00 6.00 6.75 9.00
反映数据分散程度的函数
下面是R中反映数据分散程度的函数
- range():极值
- var():反差
- sd():标准差
> a <- c(1,5,6,9,7,5,6,7,2,6)
> range(a)
[1] 1 9
> var(a)
[1] 5.6
> sd(a)
[1] 2.366432
数值摘要表
通过summary()函数我们可以得到一张表,从这张表中我们可以直接得到数据的极值、分位数、中位数、均值。
> summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 5.00 6.00 5.40 6.75 9.00
缺失值
NA缺失值
在R语言中NA表示缺失值,也就是不存在的值,或者说未知的值。
任何值与NA计算结果都是NA
> 1+NA
[1] NA
> 1*NA
[1] NA
在如果我们想将NA排除在外,可以将函数中的na.rm属性设置为TRUE
> a <- c(NA,1:49)
> a
[1] NA 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
[39] 38 39 40 41 42 43 44 45 46 47 48 49
> sum(a)
[1] NA
> mean(a)
[1] NA
> sum(a,na.rm = T)
[1] 1225
> mean(a,na.rm = T)
[1] 25
可以通用is.na函数查找缺失的值
> is.na(a)
[1] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[20] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[39] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
我们可以通过complete.cases()函数找到缺失的值
> a <- matrix(c(1:6,NA,8,9),nrow = 3)
> a
[,1] [,2] [,3]
[1,] 1 4 NA
[2,] 2 5 8
[3,] 3 6 9
> complete.cases(a)
[1] FALSE TRUE TRUE
> b <- c(1,6,NA)
> complete.cases(b)
[1] TRUE TRUE FALSE
可以通过下面的方式把缺失的行去除
> a[complete.cases(a)]
[1] 2 3 5 6 8 9
> a[complete.cases(a),]
[,1] [,2] [,3]
[1,] 2 5 8
[2,] 3 6 9
还可以直接通过na.omit()函数得到去除缺失值后的数据
> na.omit(a)
[,1] [,2] [,3]
[1,] 2 5 8
[2,] 3 6 9
attr(,"na.action")
[1] 1
attr(,"class")
[1] "omit"
下面是R语言中缺失值的解决方法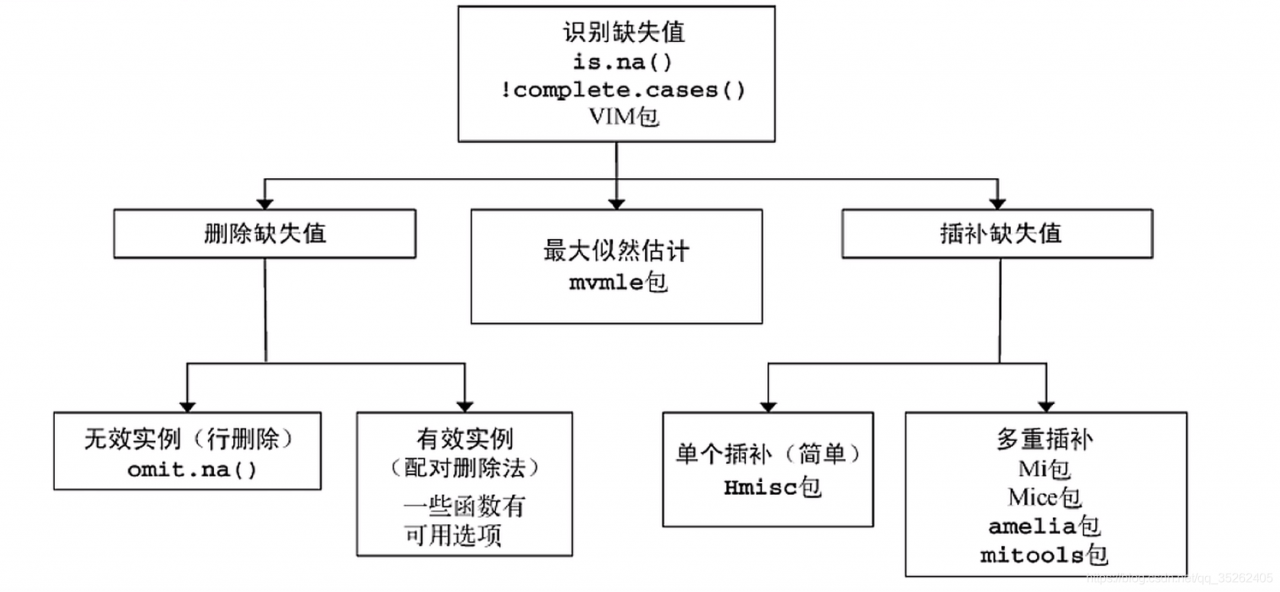
其他缺失值
- 缺失数据NaN,代表不可能的值;
- Inf表示无穷,分为正无穷Inf和负无穷Inf,代表无穷大或者无穷小。
下面是上面两种缺失值与NA缺失值的区别:
- NA是存在的值,但是不知道是多少;
- NaN是不存在的;
- Inf存在,是无穷大,-Inf是无穷小,表示的是不可能的值。
下面就是典型的NaN和Inf值
> 1/0
[1] Inf
> -1/0
[1] -Inf
> 0/0
[1] NaN
我们可以用is.infinite和is.nan函数判断这两种缺失值
> is.infinite(1/0)
[1] TRUE
> is.nan(0/0)
[1] TRUE
缺失值填充
一般通过如下的步骤实现缺失值的填充:
- 计算相关性
- 构建回归模型(lm(y~x))
- 带入回归模型预测
数据标准化
数据分析时经常需要数据标准化处理,常见的比如:回归、主成分、因子分析等,在神经网络、聚类分析中也会经常用到数据标准化预处理,甚至感觉一切的数据分析好像都需要标准化预处理。
数据标准化的作用主要时消除变量间的量纲关系,从而使数据具有可比性。
最大-最小规范化(线性变换)
y = x − m i n ( x ) m a x ( x ) − m i n ( x ) y=\frac{x-min(x)}{max(x)-min(x)}y=max(x)−min(x)x−min(x)
这样标准化后的数据范围为0<=y<=1,可以取值0和1,分别是当x取最值的时候。这是一个线性变换,因为它本身就是一个线性关系式。
z-score规范化
y = x − x ˉ σ x y=\frac{x-\bar{x}}{\sigma\scriptscriptstyle x}y=σxx−xˉ
这是用每个数据首先减去均值再除以标准差,处理后序列正负值得分布反映了数据得峰度偏度。比如:处理后序列负值居多,表明数据小于均值较多,那么均值水平就是为数不多得几个异常较大的值撑起来的。这种方法最常见,用的最多。
对数Logistic模式
y = 1 1 + e − x y=\frac{1}{1+e^{-x}}y=1+e−x1
线性回归
线性拟合的目的在于找出两个变量之间的线性关系,进而通过一个变量预测另外一个变量。下面是线性回归后方程的一般形式。
y = α + β x + ε y=\alpha+\beta x+\varepsilony=α+βx+ε
再R语言中我们线性回归一般会有如下几个步骤
- 标准化(scale)
- 线性拟合(lm)
下面是一个简单示例,数据集是iris中的Sepal.Length和Petal.Width,首先是使用scale函数将这两列数据归一化。
> head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
> sl <- scale(iris[,1])
> pw <- scale(iris[,4])
接着将这两列归一化的数据使用lm函数实现线性拟合,拟合完之后通过summary函数检测拟合的线性回归模型,从下面的分析中的Coefficients中我们发现常数项的Pr是1,这种级别是不合格的,Estimate更是一个过于小的数值,所以模型的常数项是不合格的,我们完全可以减去这个常数项。
> model <- lm(pw~sl)
> summary(model)
Call:
lm(formula = pw ~ sl)
Residuals:
Min 1Q Median 3Q Max
-1.26825 -0.47146 -0.02345 0.37243 1.61799
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.403e-15 4.713e-02 0.0 1
sl 8.179e-01 4.729e-02 17.3 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5772 on 148 degrees of freedom
Multiple R-squared: 0.669, Adjusted R-squared: 0.6668
F-statistic: 299.2 on 1 and 148 DF, p-value: < 2.2e-16
下面是去除常数项的模型,我们发现这个模型就已经合格了
> model <- lm(pw~sl-1)
> summary(model)
Call:
lm(formula = pw ~ sl - 1)
Residuals:
Min 1Q Median 3Q Max
-1.26825 -0.47146 -0.02345 0.37243 1.61799
Coefficients:
Estimate Std. Error t value Pr(>|t|)
sl 0.81794 0.04713 17.36 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5753 on 149 degrees of freedom
Multiple R-squared: 0.669, Adjusted R-squared: 0.6668
F-statistic: 301.2 on 1 and 149 DF, p-value: < 2.2e-16
所以iris中Sepal.Length和Petal.Width的线性关系大致如下
y = 0.81794 x y=0.81794 xy=0.81794x
我们可以将iris中Sepal.Length和Petal.Width的散点图发出来检查一下
> plot(pw,sl)
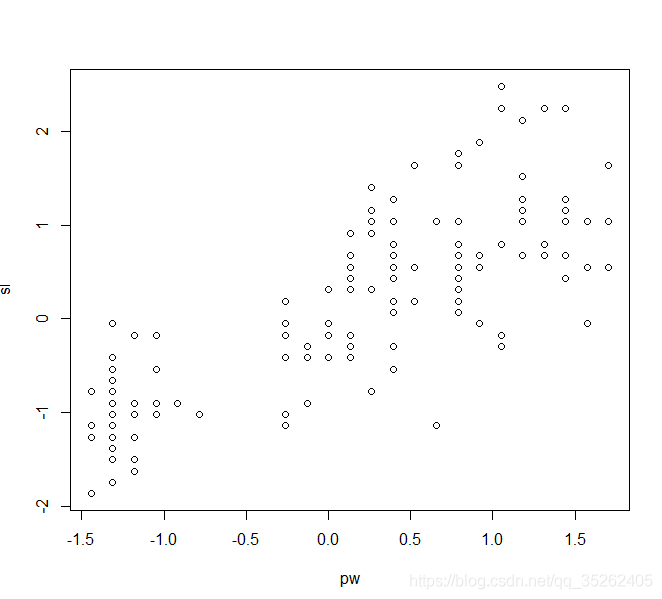
多元线性回归
对于一组变量数据,如果我们不管是通过画散点图还是其他方法,知道了一个变量与其他变量呈很强线性关系。我们就需要知道,到底是什么样的关系,关系系数是多少。
通过是用经典的最小二乘法,因为这样算出的缺失是最优的系数,可以保证残差平方和最小的优化目标。
下面就是多元线性回归后的标准模型
y = β 0 + β 1 x 1 + . . . + β k x k + ε y=\beta_0+\beta_1 x_1 +...+\beta_k x_k +\varepsilony=β0+β1x1+...+βkxk+ε
至于在R语言中多元线性回归的步骤一般如下:
- 数据标准化,
scale()函数; - 模型拟合,
lm()函数; - 残差图,
plot()函数; - 得出结果。
下面是对于R提供的iris数据集进行多元线性回归,首先还是通过scale函数实现数据标准化
> head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
> sl <- scale(iris[,1])
> sw <- scale(iris[,2])
> pl <- scale(iris[,3])
> pw <- scale(iris[,4])
接着通过lm函数进行线性拟合,通过summary分析拟合后的函数,同样发现常数项的pr值是不合格的,于是可以去除这个常数项
> model <- lm(sl~sw+pl+pw)
> summary(model)
Call:
lm(formula = sl ~ sw + pl + pw)
Residuals:
Min 1Q Median 3Q Max
-1.00012 -0.26555 0.02264 0.23802 1.02129
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.176e-16 3.102e-02 0.000 1
sw 3.426e-01 3.508e-02 9.765 < 2e-16 ***
pl 1.512e+00 1.209e-01 12.502 < 2e-16 ***
pw -5.122e-01 1.174e-01 -4.363 2.41e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3799 on 146 degrees of freedom
Multiple R-squared: 0.8586, Adjusted R-squared: 0.8557
F-statistic: 295.5 on 3 and 146 DF, p-value: < 2.2e-16
去除常数项后的模型就合格了,其中R-squared也是达到了0.8586,证明拟合的还算不错
> model <- lm(sl~sw+pl+pw-1)
> summary(model)
Call:
lm(formula = sl ~ sw + pl + pw - 1)
Residuals:
Min 1Q Median 3Q Max
-1.00012 -0.26555 0.02264 0.23802 1.02129
Coefficients:
Estimate Std. Error t value Pr(>|t|)
sw 0.34258 0.03496 9.799 < 2e-16 ***
pl 1.51175 0.12050 12.545 < 2e-16 ***
pw -0.51224 0.11701 -4.378 2.26e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3786 on 147 degrees of freedom
Multiple R-squared: 0.8586, Adjusted R-squared: 0.8557
F-statistic: 297.6 on 3 and 147 DF, p-value: < 2.2e-16
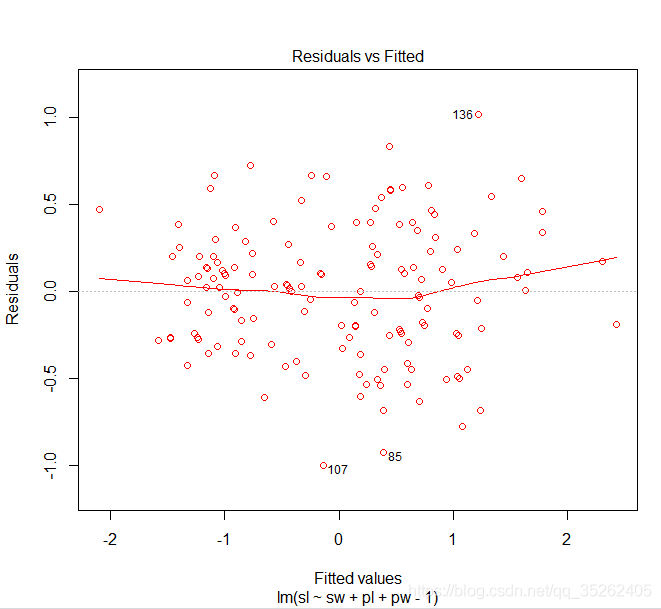
最后通过plot函数画出残差图,其中第二参数‘1’就是指定了图的类型是残差图,从下面的图中可以看出136、107、85这三个异常点。
plot(model,1,col = 'red')
通过下面的方式画出Q-Q图
plot(model,2,col = 'red')
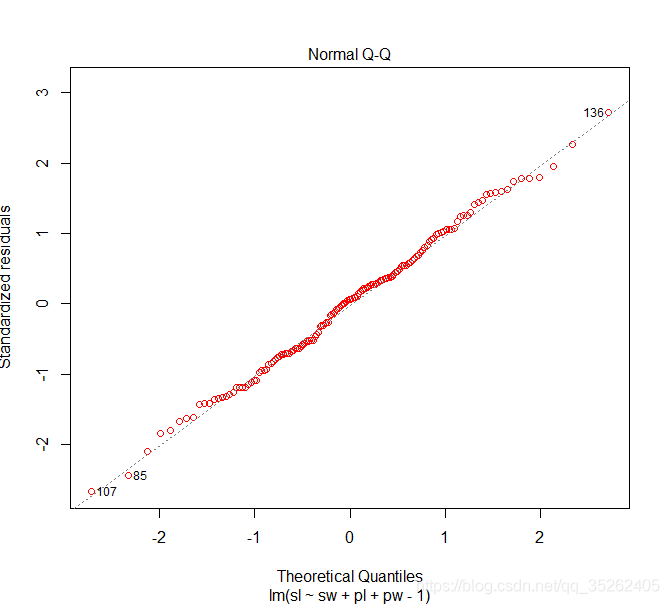
那么最后我们就可以求出线性模型如下
s l = 0.34258 s w + 1.51175 p l − 0.51224 p w sl=0.34258sw+1.51175pl-0.51224pwsl=0.34258sw+1.51175pl−0.51224pw
主成分分析
在数据分析中,我们常常会遇到高维的数据集,这时就需要降维方法,它要求被分析的变量之间具有相关性,否则就是去主成分分析的原有意义呢。
比如在学生成绩看综合评估、地区发展综合评估、运动员综合能力评估等,往往会有许多评估指标,这时候就需要进行数据降维,用较少的几个新变量代替原本的变量而尽可能保留原有的信息,计算出综合得分,进而给出综合评价结果。
主成分分析步骤如下:
- 构建原始数据矩阵;
- 消除量纲——数据标准化;
- 建立协方差矩阵(就是相关系数矩阵);
- 求出特征值、特征向量;
- 根据方差、累积方差贡献率确定主成分个数;
- 求出综合得分,给出现实意义的解释。
下面通过R提供的数据集进行了主成分分析的示例,分析的数据集是swiss数据集,这个数据集包含了瑞士的47个城市在6个评价指标上的数据。
首先还是标准化数据
> head(swiss)
Fertility Agriculture Examination Education Catholic Infant.Mortality
Courtelary 80.2 17.0 15 12 9.96 22.2
Delemont 83.1 45.1 6 9 84.84 22.2
Franches-Mnt 92.5 39.7 5 5 93.40 20.2
Moutier 85.8 36.5 12 7 33.77 20.3
Neuveville 76.9 43.5 17 15 5.16 20.6
Porrentruy 76.1 35.3 9 7 90.57 26.6
> sc <- scale(swiss)
> head(sc)
Fertility Agriculture Examination Education Catholic Infant.Mortality
Courtelary 0.8051305 -1.4820682 -0.18668632 0.1062125 -0.7477267 0.77503669
Delemont 1.0372847 -0.2447942 -1.31480509 -0.2057867 1.0477479 0.77503669
Franches-Mnt 1.7897846 -0.4825622 -1.44015162 -0.6217858 1.2529998 0.08838778
Moutier 1.2534283 -0.6234617 -0.56272591 -0.4137863 -0.1768099 0.12272023
Neuveville 0.5409551 -0.3152440 0.06400674 0.4182118 -0.8628212 0.22571757
Porrentruy 0.4769125 -0.6762990 -0.93876550 -0.4137863 1.1851420 2.28566429
接着通过princomp函数进行主成分分析
> pri <- princomp(sc,cor = TRUE)
> summary(pri,loadings = TRUE)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
Standard deviation 1.7887865 1.0900955 0.9206573 0.66251693 0.45225403 0.34765292
Proportion of Variance 0.5332928 0.1980514 0.1412683 0.07315478 0.03408895 0.02014376
Cumulative Proportion 0.5332928 0.7313442 0.8726125 0.94576729 0.97985624 1.00000000
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
Fertility 0.457 0.322 0.174 0.536 0.383 0.473
Agriculture 0.424 -0.412 -0.643 0.375 0.309
Examination -0.510 0.125 0.814 -0.224
Education -0.454 0.179 -0.532 0.681
Catholic 0.350 0.146 -0.807 0.183 -0.402
Infant.Mortality 0.150 0.811 0.160 -0.527 -0.105
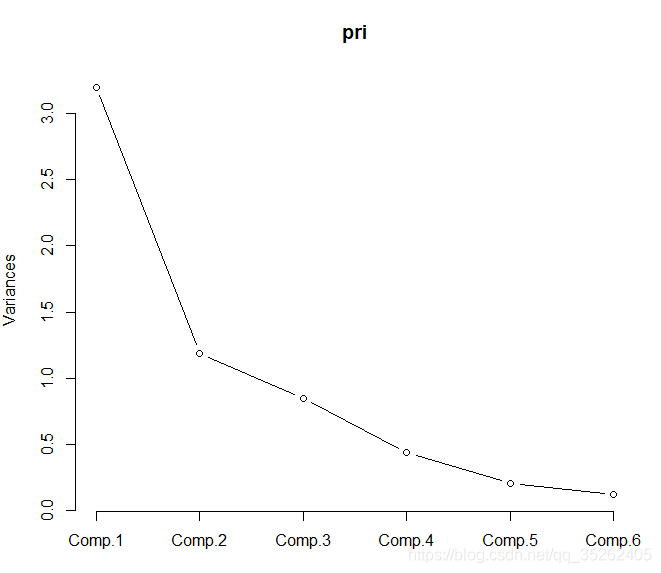
通过screeplot函数画出碎石图确定主成分个数
screeplot(pri,type = 'line')
通过predict可以查看每一个城市在每一个主成分上的得分
> predict(pri)
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
Courtelary -0.36355156 1.39942043 0.8597075 0.910963605 -0.63161039 0.28337042
Delemont 1.63417550 1.02604695 -0.5478672 0.505921909 -0.64635832 0.09123058
Franches-Mnt 2.10420020 0.74602360 -0.4726831 1.501911294 -0.40765420 0.08720438
Moutier 0.74760789 0.59589165 0.5791595 1.072298689 -0.22992758 0.30997471
Neuveville -0.38152761 0.44884479 0.6282612 0.246077409 -0.07112802 0.76731497
Porrentruy 1.36921903 2.29187838 -0.3505274 -0.307782719 -0.83653932 -0.70933512
Broye 1.72432731 1.12775240 -0.4321727 -0.467113882 0.82572488 -0.07841113
Glane 2.18253588 1.76414415 -0.3982893 -0.249441795 0.81038447 0.27042035
Gruyere 1.51766939 0.62257236 -0.7079726 0.470324290 0.20333070 -0.23034770
Sarine 0.96155561 1.89512185 -0.6647708 -0.001973985 0.30001246 -0.03329330
Veveyse 2.01128901 1.54135700 -0.4058252 -0.287603102 0.62698878 -0.12467771
Aigle -0.80506589 -1.35892381 0.3373395 -0.077269309 0.43968807 0.27674183
Aubonne 0.17520904 -0.88187440 0.8329215 -0.504185854 -0.18845018 0.29393399
Avenches -0.23562425 0.48914597 0.8083984 -0.961529850 0.11736633 0.37875429
Cossonay -0.42035821 -1.07192701 0.9281662 -0.741320000 0.53774346 -0.24555932
Echallens 0.59889560 -0.30086168 0.8578256 -0.896887294 0.41147631 -0.32192730
Grandson -0.46581609 0.18010264 0.9661629 0.469430116 -0.32477593 -0.02954850
Lausanne -2.78442448 0.63703185 -0.4103685 -0.088366571 -0.25421374 0.24241992
La Vallee -3.42909196 -2.07525184 -0.2448720 1.712934307 0.50503356 -0.24296878
Lavaux -0.15436533 -0.65730064 0.7829503 -0.957702534 0.31825529 0.27298746
Morges -0.71390686 -0.89333076 0.6319530 -0.222216266 0.49554378 0.12182041
Moudon 0.25236121 0.15735119 1.1905959 -0.788599650 -0.53396422 -0.34277056
Nyone -1.29000159 -1.25551410 0.1440459 -0.112175353 0.14726464 -0.26088870
Orbe -0.94982763 -1.87067448 0.5986589 0.135712308 0.06640493 -0.41608229
Oron 0.96765998 -0.41301362 1.3210597 -0.639169876 -0.18274004 0.13599047
Payerne 0.48915287 0.83286698 1.0989038 -0.781155988 -0.28389870 0.36523538
Paysd'enhaut 0.94131433 -1.18635377 0.9760593 0.129231998 -0.85124791 0.40058569
Rolle -0.55958462 -1.60672774 0.3474346 -0.109333221 -0.18906898 0.13423051
Vevey -1.96390503 0.60351152 0.0204286 -0.201054029 -0.08290364 -0.25217038
Yverdon -0.12335657 0.41402839 0.9121602 -0.683585317 -0.54601214 -0.09292530
Conthey 2.40893922 -2.04463449 -1.0525424 0.435254058 -0.13443293 -0.01610155
Entremont 1.95527998 -0.72627044 -1.0539122 -0.732645507 -0.13130720 -0.21572130
Herens 2.58674740 -1.13381204 -0.8384683 -0.193564929 0.07632329 -0.03741754
Martigwy 1.52334927 -0.60823624 -0.9759511 -0.452038974 0.32125628 -0.38639558
Monthey 2.10281914 -0.04580606 -0.6590874 0.231413249 -0.15043867 -0.31480419
St Maurice 1.24475999 -1.15053479 -1.3427985 -0.341854259 -0.16118089 -0.28819025
Sierre 3.01438790 -1.22991180 -0.7999096 0.965963131 0.30940289 0.64810996
Sion 1.07917226 -0.32825283 -1.2372365 0.515352351 0.43036016 0.26994007
Boudry -1.16783772 0.37614158 0.7918458 0.134884925 0.60627472 -0.01839639
La Chauxdfnd -1.98754750 0.92983063 0.7201498 0.782338582 0.29429897 -0.86160681
Le Locle -1.30711318 0.41467405 0.5717183 1.142289944 -0.02910645 -0.06177060
Neuchatel -3.08273842 1.91976852 -0.3432797 -0.263154993 0.80372214 0.46212052
Val de Ruz 0.01142719 0.22331275 1.0431698 0.650169028 -0.27322389 0.21462817
ValdeTravers -1.35578566 0.33954785 0.9506714 0.788888804 0.16757825 -0.73452003
V. De Geneve -5.65565803 0.56333827 -2.6557725 -0.321439701 -0.03847105 0.43944741
Rive Droite -1.85826599 -0.71488255 -1.6434878 -0.826611433 -0.93783867 0.22876851
Rive Gauche -2.54870102 0.01438935 -1.6619528 -0.591583605 -0.69794132 -0.37939969
> pre <- predict(pri)
> summary(pre)
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
Min. :-5.65566 Min. :-2.0753 Min. :-2.6558 Min. :-0.9615 Min. :-0.93784
1st Qu.:-1.05883 1st Qu.:-0.8876 1st Qu.:-0.6619 1st Qu.:-0.4856 1st Qu.:-0.26372
Median : 0.01143 Median : 0.1801 Median : 0.1440 Median :-0.1122 Median :-0.03847
Mean : 0.00000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.00000
3rd Qu.: 1.44344 3rd Qu.: 0.6298 3rd Qu.: 0.8207 3rd Qu.: 0.4699 3rd Qu.: 0.31976
Max. : 3.01439 Max. : 2.2919 Max. : 1.3211 Max. : 1.7129 Max. : 0.82572
Comp.6
Min. :-0.8616
1st Qu.:-0.2489
Median :-0.0184
Mean : 0.0000
3rd Qu.: 0.2717
Max. : 0.7673
通过eigen函数求出特征值
> y <- eigen(cor(sc))
> y
eigen() decomposition
$values
[1] 3.1997570 1.1883082 0.8476098 0.4389287 0.2045337 0.1208626
$vectors
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.4569876 0.3220284 0.17376638 0.53555794 0.38308893 0.47295441
[2,] 0.4242141 -0.4115132 -0.03834472 -0.64291822 0.37495215 0.30870058
[3,] -0.5097327 0.1250167 0.09123696 -0.05446158 0.81429082 -0.22401686
[4,] -0.4543119 0.1790495 -0.53239316 -0.09738818 -0.07144564 0.68081610
[5,] 0.3501111 0.1458730 -0.80680494 0.09947244 0.18317236 -0.40219666
[6,] 0.1496668 0.8111645 0.16010636 -0.52677184 -0.10453530 -0.07457754
最后算出最终得分
> scores <- (y$values[1]*pre[,1]+y$values[2]*pre[,2]+y$values[3]*pre[,3]+y$values[4]*pre[,4])/sum(y$values[1:4])
> scores
Courtelary Delemont Franches-Mnt Moutier Neuveville Porrentruy Broye
0.2869294213 1.0936288874 1.3882936724 0.7157910349 -0.0082646920 1.1758391149 1.1077782013
Glane Gruyere Sarine Veveyse Aigle Aubonne Avenches
1.5213133496 0.9167750940 0.8396005716 1.3740209884 -0.6941135000 -0.0004619647 0.0159445934
Cossonay Echallens Grandson Lausanne La Vallee Lavaux Morges
-0.3802005799 0.3334569108 -0.0443212193 -1.5047941538 -2.2722291113 -0.1818160506 -0.5124178520
Moudon Nyone Orbe Oron Payerne Paysd'enhaut Rolle
0.2920905295 -0.9774729513 -0.8273984483 0.6070348886 0.5539493267 0.4381388293 -0.6085575824
Vevey Yverdon Conthey Entremont Herens Martigwy Monthey
-0.9935132584 0.1005168014 0.8066227226 0.7363513573 1.0809547212 0.5508643287 1.0955837231
St Maurice Sierre Sion Boudry La Chauxdfnd Le Locle Neuchatel
0.2339406861 1.3974142570 0.3948350736 -0.4510347744 -0.7579290047 -0.4764572464 -1.4078887244
Val de Ruz ValdeTravers V. De Geneve Rive Droite Rive Gauche
0.2593145665 -0.4903660180 -3.4926597035 -1.5069528518 -1.7281339644