曲率圆中心坐标公式_流形微分几何(5)——曲率

我不知道大家学没学曲线论和曲面论，但我就当大家学了，我以后可能会把这种

$equation?tex=E3$ 微分几何的内容写一下。另外上期有同学说要讲相流，那么下节我就把相流放在单参群里讲一下吧。

一、曲面上的测地线

考虑在曲面

$equation?tex=S%3A%5Cbm+r%3D%5Cbm+r%28u%2Cv%29$ 上的曲线

$equation?tex=C%3A%5Cbm+r%28t%29%3D%5Cbm+r%5Bu%28t%29%2Cv%28t%29%5D$ ，我们知道

$equation?tex=%5Cfrac%7Bd%5E2%5Cbm+r%7D%7Bdt%5E2%7D%3Dk%5Cbm%5Cbeta$ ，其中

$equation?tex=k$ 为曲率，

$equation?tex=%5Cbm%5Cbeta$ 为主法方向。

注意到

$equation?tex=k%5Ccos%5Ctheta%3Dk%5Cbm%5Cbeta%5Ccdot%5Cbm+n%3D%5Cbm+n%5Ccdot%5Cfrac%7Bd%5E2%5Cbm+r%7D%7Bdt%5E2%7D$

如果采用自然参数

$equation?tex=t%3Ds$ ，那么

$equation?tex=k%5Ccos%5Ctheta%3D%5Cfrac%7B%5Cbm+n%5Ccdot+d%5E2%5Cbm+r%7D%7Bds%5E2%7D%3D%5Cfrac%7BII%7D%7BI%7D$

其中

$equation?tex=I%2CII$ 为曲面

$equation?tex=S$ 的第一、第二基本形式。

我们用

$equation?tex=k_n%3Dk%5Ccos%5Ctheta%3DII%2FI$ 叫做曲面

$equation?tex=S$ 沿着方向

$equation?tex=%5Cbm+r%27%28s%29$ 的

法曲率。

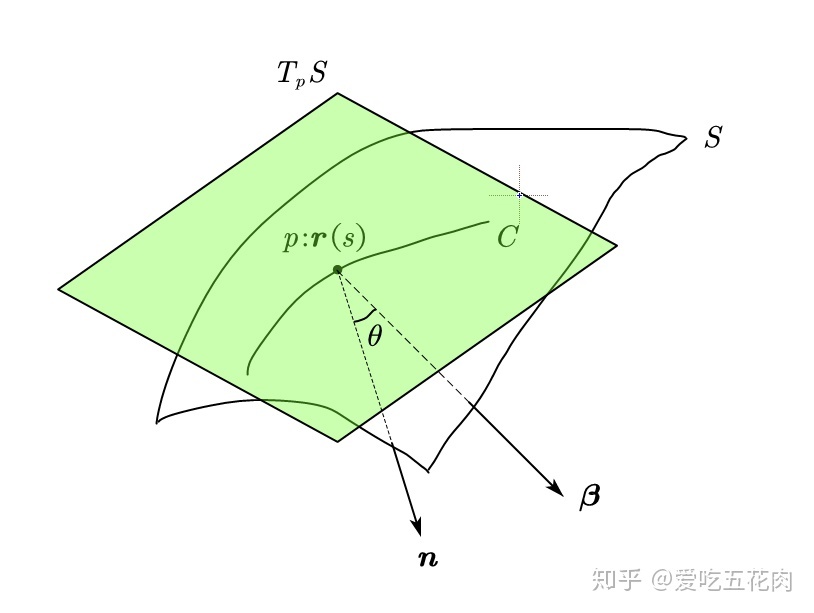
（笔记本画图真麻烦）

我们仔细看看这个图，如果令

$equation?tex=C%27$ 为

$equation?tex=C$ 在切平面

$equation?tex=T_p+S$ 上的投影曲线，那么

$equation?tex=C%E7%9A%84%E6%9B%B2%E7%8E%87k%5Cbm%5Cbeta%5Cto+C%27%E7%9A%84%E6%9B%B2%E7%8E%87k_n%5Cbm+n$

能不能理解？

当然证明是简单的（^_^。。。），留给读者（我错了）

大家看我画出投影曲线

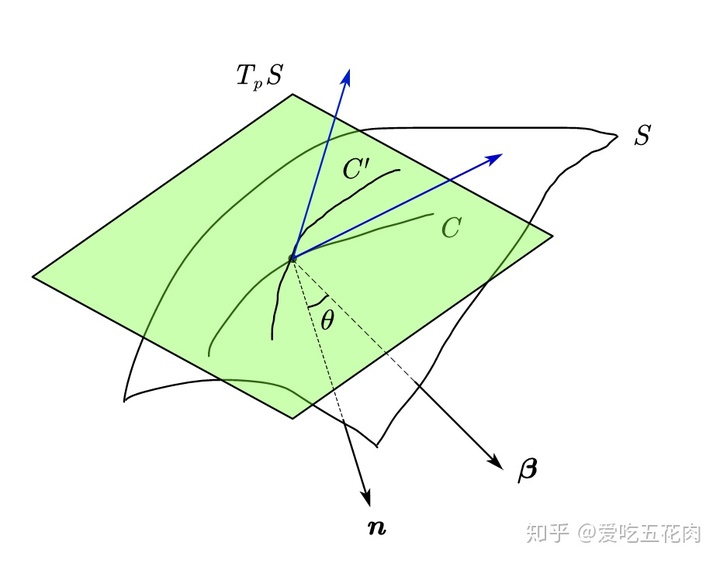
两条蓝线分别为

$equation?tex=C%2CC%27$ 的切方向，明显它们都在

$equation?tex=T_pS$ 上，夹角为

$equation?tex=%5Ctheta$ 。

那么明显

$equation?tex=%5Cbm+n$ 就是

$equation?tex=C%27$ 的主法矢量，这就出来了。

这个关系叫做Meusnier定理，大家可以在上图的基础上画出

$equation?tex=C$ 和

$equation?tex=C%27$ 的曲率圆（。。。），这样会更直观，但我不想画了，笔记本鼠标贼难受。

曲面上如果某个方向的

$equation?tex=d%5Cbm+r%2F%2Fd%5Cbm+n$ （就是比较平，比如平面就满足），那么这个方向叫做

主方向。沿着主方向的法曲率叫做 主曲率。注意，正交的

$equation?tex=u%2Cv$ 曲线为主方向，因为

$equation?tex=%5Cgamma_u%3Adv%3D0%2C%5Cgamma_v%3Adu%3D0$

那么设

$equation?tex=k_1%2Ck_2$ 为坐标网的主曲率，

$equation?tex=%5Ctheta$ 为对

$equation?tex=u$ 曲线的夹角（对

$equation?tex=v$ 曲线就是余角

$equation?tex=%5Cpi%2F2-%5Ctheta$ ），那么有

$equation?tex=k_n%3Dk_1%5Ccos%5E2%5Ctheta%2Bk_2%5Csin%5E2%5Ctheta$ （Euler公式，证明挺容易的，设出形式

$equation?tex=I%2CII$ 直接算就行了）

如果我们令

$equation?tex=%5Cphi%3D%5Cpi%2F2-%5Ctheta$ ，那么

$equation?tex=k_n%3Dk_1%5Ccos%5E2%5Ctheta%2Bk_2%5Ccos%5E2%5Cphi%3D%28k_1%5Ccos%5Ctheta%29%5Ccos%5Ctheta%2B%28k_2%5Ccos%5Cphi%29%5Ccos%5Cphi%3Dk_%7Bn1%7D%5Ccos%5Ctheta%2Bk_%7Bn2%7D%5Ccos%5Cphi$

这是啥？对，这说明曲率是符合矢量的三角形法则的，所以我们就可以规定所谓的矢量法曲率

$equation?tex=%5Cbm+k_n%3Dk_n%5Cbm+n$ 。（顺便一提，上面的式子也叫Euler公式。。。数学上有很多Euler公式，就像有很多Gauss定理一样）

其实，物理上的加速度定义为

$equation?tex=%5Cbm+a%3D%5Cfrac%7Bd%5E2%5Cbm+r%7D%7Bdt%5E2%7D%3D%5Cfrac%7Bd%5E2%5Cbm+r%7D%7Bds%5E2%7D%5Cfrac%7Bds%5E2%7D%7Bdt%5E2%7D%3D%5Cbm+k%5Cgamma%5E2$

其中

$equation?tex=%5Cgamma%3Dds%2Fdt$ ，明显的

$equation?tex=a%3D%5Cgamma%5E2%2C%5Cbm+k%3D%5Cbm+a%2F%7C%7C%5Cbm+a%7C%7C$ ，对吧，这就是矢量曲率的最基本形式，即曲率乘上主法矢量

$equation?tex=%5Cbm+k%3Dk%5Cbm%5Cbeta$ 。

此外，我们还会用到Gauss曲率

$equation?tex=K%3Dk_1k_2$ 和平均曲率

$equation?tex=H%3D%5Cfrac%7Bk_1%2Bk_2%7D%7B2%7D$ ，我们考虑

$equation?tex=K%3D0$ 和

$equation?tex=H%3D0$ 的曲面。注意若

$equation?tex=K%3D0$ ，只要

$equation?tex=k_1%2Ck_2$ 一个为零就可以了，假设

$equation?tex=k_1%3D0$ ，这说明曲面在

$equation?tex=u$ 方向是直的，那么可以将其看成是平面沿着

$equation?tex=v$ 方向卷起来的，对

$equation?tex=k_2%3D0$ 同理，这种曲面叫做

可展曲面。

$equation?tex=H%3D0$ 的曲面叫做

极小曲面，这是因为存在一个定理：给定曲面

$equation?tex=S$ 的边界

$equation?tex=%5Cpartial+S$ ，则若

$equation?tex=H_S%3D0$ 则曲面

$equation?tex=S$ 的表面积取最小值（注意不是极小值），证明自己去看微分几何的教科书（这可以看成两点之间直线最短的一般情况）。

曲面上曲线沿着切平面的投影具有重要意义，如果曲面曲线

$equation?tex=C%5Csubset+S$ 在每点

$equation?tex=%5Cforall+p%5Cin+C$ 上的切平面

$equation?tex=T_p+S$ 上的投影曲线

$equation?tex=C_p%27$ 都在

$equation?tex=p$ 点曲率为0（在

$equation?tex=p$ 点附近为直线），那么这段曲线就比较直，我们将其称为

测地线。对于一个曲面曲线，我们把其在切平面的投影曲线的曲率叫做 测地曲率

$equation?tex=k_g$ ，也就是说测地线是处处

$equation?tex=k_g%5Cequiv+0$ 的曲线。

容易看出

$equation?tex=k%5E2%3Dk_g%5E2%2Bk_n%5E2$ ，或者说

$equation?tex=%5Cbegin%7Bcases%7D%5Cbm+k%3D%5Cbm+k_g%2B%5Cbm+k_n%5C%5C+%5Cbm+k_g%5Cbot%5Cbm+k_n%5Cend%7Bcases%7D$ ，看下图

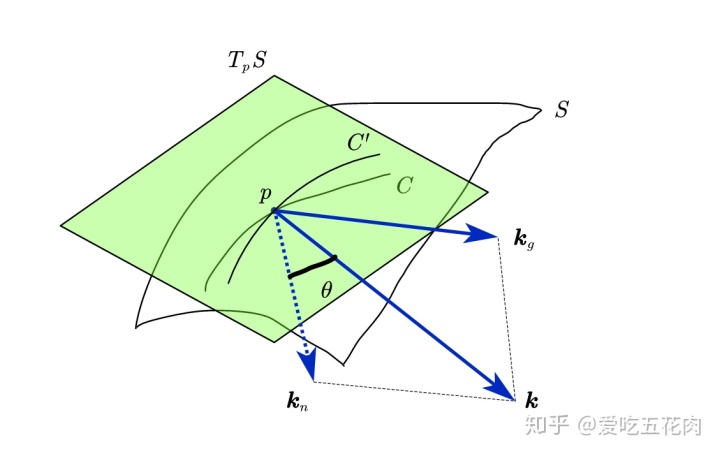
是不是简洁明了？注意蓝色的箭头是曲率矢量，

$equation?tex=%5Cbm+k_n$ 是向下穿过去的。那么对测地线，

$equation?tex=%5Cbm+k_g%3D0$ ，那么只有

$equation?tex=%5Cbm+k%3D%5Cbm+k_n%5C+%5Cbot%5C++T_p+S$ 了，对吧。

二、Christoffel记号

这种记号的优势是可以直接推向高维情况——流形，所以我们引入指标记号来表示曲面

$equation?tex=S%3A%5Cbm+r%3D%5Cbm+r%28u%5E1%2Cu%5E2%29$

偏导数就写成

$equation?tex=%5Cpartial_k%3D%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+u%5Ek%7D$ ，

$equation?tex=%5Cbm+r_i%3D%5Cpartial_i%5Cbm+r$ ，

$equation?tex=%5Cbm+r_%7Bij%7D%3D%5Cpartial_i%5Cpartial_j%5Cbm+r$ ，由此

$equation?tex=%5Cbm+n%3D%5Cfrac%7B%5Cbm+r_1%5Ctimes%5Cbm+r_2%7D%7B%5Csqrt%7B%5C+g%5C+%7D%7D$

并且我们把第一基本量表示成度规的系数

$equation?tex=g_%7Bij%7D%3D%5Cbm+r_i%5Ccdot%5Cbm+r_j%5Cto%5Cbegin%7Bcases%7DE%3Dg_%7B11%7D%5C%5CF%3Dg_%7B12%7D%3Dg_%7B21%7D%5C%5C+G%3Dg_%7B22%7D%5Cend%7Bcases%7D$

并且

$equation?tex=g%3D%5Cdet%7Ca_%7Bij%7D%7C%3DEG-F%5E2$

第二基本量表示为

$equation?tex=L_%7Bij%7D%3D%5Cbm+r_%7Bij%7D%5Ccdot%5Cbm+n$ 。

下面我们尝试把

$equation?tex=D%5E2%5Cbm+r$ 和

$equation?tex=D%5Cbm+n$ 分别用

$equation?tex=%28D%5Cbm+r%2C%5Cbm+n%29$ 和

$equation?tex=D%5Cbm+r$ 线性表示，其中

$equation?tex=D$ 为某个微分算子，我们待定系数为

$equation?tex=%5Cbegin%7Bcases%7D+%5Cbm+r_%7Bij%7D%3D%5CGamma%5Ek_%7Bij%7D%5Cbm+r_k%2B%5Clambda_%7Bij%7D%5Cbm+n%5C%5C+%5Cbm+n_i%3D%5Cmu_i%5Ej%5Cbm+r_j+%5Cend%7Bcases%7D$

第一式点乘

$equation?tex=%5Cbm+n$ 得到

$equation?tex=L_%7Bij%7D%3D%5Clambda_%7Bij%7D%5Cbm+n%5E2%3D%5Clambda_%7Bij%7D$ （法向量已经归一化）

下面尝试定出

$equation?tex=%5CGamma_%7Bij%7D%5Ek$ ，为此我们有

$equation?tex=g_%7Bij%7D%3D%5Cbm+r_i%5Ccdot%5Cbm+r_j%5Cto%5Cpartial_lg_%7Bij%7D%3D%5Cbm+r_%7Bil%7D%5Ccdot%5Cbm+r_j%2B%5Cbm+r_i%5Ccdot%5Cbm+r_%7Bjl%7D$

轮换上式可以得到如下的关系式

$equation?tex=%5Cfrac%7B1%7D%7B2%7D%5Cleft%28%5Cfrac%7B%5Cpartial+g_%7Bil%7D%7D%7B%5Cpartial+u%5Ej%7D%2B%5Cfrac%7B%5Cpartial+g_%7Bjl%7D%7D%7B%5Cpartial+u%5Ei%7D-%5Cfrac%7B%5Cpartial+g_%7Bij%7D%7D%7B%5Cpartial+u%5El%7D%5Cright%29%3D%5CGamma_%7Bij%7D%5Ekg_%7Bkl%7D%5Cquad%281%29$

消去度规（用逆矩阵

$equation?tex=g%5E%7Bij%7D$ ）得到

$equation?tex=%5CGamma_%7Bij%7D%5Ek%3D%5Cfrac%7B1%7D%7B2%7Dg%5E%7Bkl%7D%5Cleft%28%5Cfrac%7B%5Cpartial+g_%7Bil%7D%7D%7B%5Cpartial+u%5Ej%7D%2B%5Cfrac%7B%5Cpartial+g_%7Bjl%7D%7D%7B%5Cpartial+u%5Ei%7D-%5Cfrac%7B%5Cpartial+g_%7Bij%7D%7D%7B%5Cpartial+u%5El%7D%5Cright%29%5Cquad+%282%29$

我们把(1)式叫做第一类Christoffel符号

$equation?tex=%5Bij%2Cl%5D%3D%5CGamma_%7Bij%7D%5Ekg_%7Bkl%7D$ ，把(2)式叫做第二类Christoffel符号

$equation?tex=%5Cbegin%7BBmatrix%7Dk%5C%5Cij%5Cend%7BBmatrix%7D$ ，但我们保留

$equation?tex=%5CGamma_%7Bij%7D%5Ek$ 的记号叫做Christoffel记号。

至于

$equation?tex=%5Cmu_i%5Ej$ ，可以定出

$equation?tex=%5Cmu_i%5Ej%3D-g%5E%7Bjk%7DL_%7Bik%7D$ ，具体留作练习

由此我们得到Gauss-Weingarten方程组

$equation?tex=%5Cbegin%7Bcases%7D+%5Cbm+r_%7Bij%7D%3D%5CGamma%5Ek_%7Bij%7D%5Cbm+r_k%2BL_%7Bij%7D%5Cbm+n%5C%5C+%5Cbm+n_i%3D-g%5E%7Bjk%7DL_%7Bik%7D%5Cbm+r_j+%5Cend%7Bcases%7D$

三、张量曲率——曲面的Riemann曲率

我们前面提到过，曲面的曲率有很多，比如法曲率、Gauss曲率、平均曲率、测地曲率等等等等，这和曲线完全不同，这是为什么呢？因为曲面比曲线整整高了一个自由度！曲面的各种曲率都是不完整的表达，完整的表达是Riemann曲率，这是一个张量，定义为

$equation?tex=R_%7Bijk%7D%5El%3D%5Cpartial_k%5CGamma%5El_%7Bij%7D-%5Cpartial_j%5CGamma%5El_%7Bik%7D%2B%5CGamma_%7Bij%7D%5Ep%5CGamma_%7Bpk%7D%5El-%5CGamma_%7Bik%7D%5Ep%5CGamma_%7Bpj%7D%5El$

别忘了后面的Einstein求和，这个式子可以形式的写成这样

$equation?tex=R%5Cto%5Cbegin%7BVmatrix%7D%5Cpartial_k%26%5Cpartial_j%5C%5C%5CGamma%5El_%7Bik%7D%26%5CGamma%5El_%7Bij%7D%5Cend%7BVmatrix%7D%2B%5Cbegin%7BVmatrix%7D%5CGamma%5E%7B%5Ccolor%7Bblue%7D%7B%5Cbm+p%7D%7D_%7Bij%7D%26%5CGamma%5E%7B%5Ccolor%7Bblue%7D%7B%5Cbm+p%7D%7D_%7Bik%7D%5C%5C%5CGamma%5El_%7B%7B%5Ccolor%7Bblue%7D%7B%5Cbm+p%7D%7Dj%7D%26%5CGamma%5El_%7B%7B%5Ccolor%7Bblue%7D%7B%5Cbm+p%7D%7Dk%7D%5Cend%7BVmatrix%7D$ （蓝色的表示求和）

当然我们有时也把上指标降下来

$equation?tex=R_%7Bmijk%7D%3Dg_%7Bml%7DR%5El_%7Bijk%7D$

我们讨论Gauss-Weingarten方程组，通过一定的数学运算可以化成Gauss-Codazzi-Mainardi方程组

$equation?tex=%5Cbegin%7Bcases%7DR_%7Bmijk%7D%3DL_%7Bij%7DL_%7Bmk%7D-L_%7Bik%7DL_%7Bmj%7D%5C%5C%5Cpartial_kL_%7Bij%7D-%5Cpartial_jL_%7Bik%7D%3D%5CGamma%5El_%7Bik%7DL_%7Blj%7D-%5CGamma_%7Bij%7D%5ElL_%7Blk%7D%5Cend%7Bcases%7D$

观察第一个式子，我们注意到

$equation?tex=R_%7B1212%7D%3DL_%7B12%7DL_%7B12%7D-L_%7B11%7DL_%7B22%7D%3D-Kg%5Cto+K%3D-R_%7B1212%7D%2Fg$

下面我们看看如何在Euclid空间E

$equation?tex=E%5En$ 上建立Riemann曲率

考虑一个矢量场

$equation?tex=%5Cbm+v$ 在两个坐标系

$equation?tex=%5C%7Bx%5Ei%5C%7D$ 和

$equation?tex=%5C%7By%5Ei%5C%7D$ 下的表达式

$equation?tex=%5Cbm+v%3Dv%5Ei%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+x%5Ei%7D%3D%5Ctilde%7Bv%7D%5Ei%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+y%5Ei%7D$

我们知道，坐标变换就相差两个坐标系的Jacobi行列式

$equation?tex=%5Ctilde%7Bv%7D%5Ei%3Dv%5Ej%5Cfrac%7B%5Cpartial+y%5Ei%7D%7B%5Cpartial+x%5Ej%7D$

我们对这个式子微分

$equation?tex=d%5Ctilde%7Bv%7D%5Ei%3Ddv%5Ej%5Cfrac%7B%5Cpartial+y%5Ei%7D%7B%5Cpartial+x%5Ej%7D%2Bv%5Ejd%5Cleft%28%5Cfrac%7B%5Cpartial+y%5Ei%7D%7B%5Cpartial+x%5Ej%7D%5Cright%29$ （简单的Leibniz法则）

后面的全微分展开得到

$equation?tex=d%5Cleft%28%5Cfrac%7B%5Cpartial+y%5Ei%7D%7B%5Cpartial+x%5Ej%7D%5Cright%29%3D%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+x%5Ek%7D%5Cfrac%7B%5Cpartial+y%5Ei%7D%7B%5Cpartial+x%5Ej%7Ddx%5Ek$

代入上式得到

$equation?tex=d%5Ctilde%7Bv%7D%5Ei%3Ddv%5Ej%5Cfrac%7B%5Cpartial+y%5Ei%7D%7B%5Cpartial+x%5Ej%7D%2Bv%5Ej%5Cfrac%7B%5Cpartial%5E2+y%5Ei%7D%7B%5Cpartial+x%5Ej%5Cpartial+x%5Ek%7Ddx%5Ek$

下面考虑流形

$equation?tex=M$ ，若存在度规

$equation?tex=%5Cbm+g$ ，或者说

$equation?tex=M$ 为一个Riemann流形，其某区域两个坐标卡

$equation?tex=%5C%7Bx%5C%7D%2C%5C%7By%5C%7D$ ，设

$equation?tex=g_%7Bij%7D%3D%5Cbm+g%5Cleft%28%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+x%5Ei%7D%2C%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+x%5Ej%7D%5Cright%29%2C%5Ctilde+g_%7Bij%7D%3D%5Cbm+g%5Cleft%28%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+y%5Ei%7D%2C%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+y%5Ej%7D%5Cright%29$

那么

$equation?tex=g_%7Bij%7D%3D%5Ctilde%7Bg%7D_%7Brs%7D%5Cfrac%7B%5Cpartial+y%5Er%7D%7B%5Cpartial+x%5Ei%7D%5Cfrac%7B%5Cpartial+y%5Es%7D%7B%5Cpartial+x%5Ej%7D%5Cto%5CGamma%5Ek_%7Bij%7D%3D%5Ctilde%7B%5CGamma%7D%5El_%7Brs%7D%5Cfrac%7B%5Cpartial+y%5Er%7D%7B%5Cpartial+x%5Ei%7D%5Cfrac%7B%5Cpartial+y%5Es%7D%7B%5Cpartial+x%5Ej%7D%5Cfrac%7B%5Cpartial+x%5Ek%7D%7B%5Cpartial+y%5El%7D%2B%5Cfrac%7B%5Cpartial%5E2+y%5El%7D%7B%5Cpartial+x%5Ei%5Cpartial+x%5Ej%7D%5Cfrac%7B%5Cpartial+x%5Ek%7D%7B%5Cpartial+y%5El%7D$

代入上式得到

$equation?tex=%28d%5Ctilde+v%5Ei%2B%5Ctilde+v%5Er%5Ctilde%5CGamma%5Ei_%7Brs%7Ddy%5Es%29%3D%28dv%5Ej%2Bv%5Ep%5CGamma%5Ej_%7Bpq%7Ddx%5Eq%29%5Cfrac%7B%5Cpartial+y%5Ei%7D%7B%5Cpartial+x%5Ej%7D$

由此，我们令

$equation?tex=Dv%5Ei%3Ddv%5Ei%2Bv%5Er%5CGamma%5Ei_%7Brs%7Ddx%5Es$ ，

$equation?tex=D%5Cbm+v%3DDv%5Ei%5Cpartial_i$

那么

$equation?tex=D%5Ctilde+v%5Ei%3DDv%5Ej%5Cfrac%7B%5Cpartial+y%5Ei%7D%7B%5Cpartial+x%5Ej%7D$ 服从反变规律，我们把这种导数叫做

协变微分。

我们知道，

$equation?tex=D%5Cbm+v$ 实际上不是向量，而是以一阶微分形式为分量的形式向量，所以我们令

$equation?tex=D_%7B%5Cbm+X%7D%5Cbm+v%3DD%5Cbm+v%28%5Cbm+X%29%3D%5Cbm+X%28Dv%5Ei%29%5Cpartial_i$

叫做

$equation?tex=%5Cbm+v$ 沿着方向

$equation?tex=%5Cbm+X$ 的协变导数，且明显地有

$equation?tex=D_%7B%5Cpartial_j%7D%5Cpartial_i%3D%5CGamma%5Ek_%7Bij%7D%5Cpartial_k$ 。

根据协变导数我们定义这么一个张量

$equation?tex=%5Cbm+R%5Cin%5Cmathscr+F_M%281%2C3%29$

$equation?tex=%5Cbm+R%28%5Cbm+u%2C%5Cbm+v%29%3A%5Cbm+t%5Cto+D_%7B%5Cbm+u%7DD_%7B%5Cbm+v%7D%5Cbm+t-D_%7B%5Cbm+v%7DD_%7B%5Cbm+u%7D%5Cbm+t-D_%7B%5B%5Cbm+u%2C%5Cbm+v%5D%7D%5Cbm+t$

我们计算其分量

$equation?tex=R%5El_%7Bijk%7D%3Ddx%5El%5Cleft%5C%7B%5B%5Cbm+R%28%5Cpartial_i%2C%5Cpartial_j%29%5D%28%5Cpartial_k%29%5Cright%5C%7D$

$equation?tex=%3Ddx%5El%5Cbigg%5BD_%7B%5Cpartial_i%7DD_%7B%5Cpartial_j%7D%5Cpartial_k-D_%7B%5Cpartial_j%7DD_%7B%5Cpartial_i%7D%5Cpartial_k%2BD_%7B%28%5Cpartial_i%5Cpartial_j-%5Cpartial_j%5Cpartial_i%29%7D%5Cpartial_k%5Cbigg%5D$

注意到偏导数可交换

$equation?tex=%5Cpartial_i%5Cpartial_j-%5Cpartial_j%5Cpartial_i%3D0$ ，则上式可化为

$equation?tex=dx%5El%5Cbigg%28D_%7B%5Cpartial_i%7DD_%7B%5Cpartial_j%7D%5Cpartial_k-D_%7B%5Cpartial_j%7DD_%7B%5Cpartial_i%7D%5Cpartial_k%5Cbigg%29%3Ddx%5El%5Cleft%28D_%7B%5Cpartial_i%7D%5CGamma%5Em_%7Bkj%7D%5Cpartial_m-D_%7B%5Cpartial_j%7D%5CGamma%5Em_%7Bki%7D%5Cpartial_m%5Cright%29$

$equation?tex=%3D%5Cleft%28D_%7B%5Cpartial_i%7D%5CGamma%5El_%7Bkj%7D%5Cpartial_l-D_%7B%5Cpartial_j%7D%5CGamma%5El_%7Bki%7D%5Cpartial_l%5Cright%29%5Cpartial_l%2B%28%E5%AF%B9m%E7%9A%84%E6%B1%82%E5%92%8C%E9%A1%B9%29%5Cquad%28%E5%AF%B9l%E5%8F%AA%E5%AF%B9%E6%8B%AC%E5%8F%B7%E5%A4%96%5Cpartial_l%E6%B1%82%E5%92%8C%29$

$equation?tex=%3D%28D_%7B%5Cpartial_i%7D%5CGamma%5El_%7Bkj%7D-D_%7B%5Cpartial_j%7D%5CGamma%5El_%7Bki%7D%2B%5CGamma%5Em_%7Bkj%7DD_%7B%5Cpartial_i%7D%5Cpartial_m-%5CGamma%5Em_%7Bki%7DD_%7B%5Cpartial_j%7D%5Cpartial_m%29%5Cpartial_l$

$equation?tex=%3D%5Cleft%28%5Cfrac%7B%5Cpartial%5CGamma%5El_%7Bkj%7D%7D%7B%5Cpartial+x%5Ei%7D-%5Cfrac%7B%5Cpartial%5CGamma%5El_%7Bki%7D%7D%7B%5Cpartial+x%5Ej%7D%2B%5CGamma%5Em_%7Bkj%7D%5CGamma%5El_%7Bmi%7D%2B%5CGamma%5Em_%7Bki%7D%5CGamma%5El_%7Bmj%7D%5Cright%29%5Cpartial_l$

即

$equation?tex=R%5El_%7Bkij%7D%3D%5Cfrac%7B%5Cpartial%5CGamma%5El_%7Bkj%7D%7D%7B%5Cpartial+x%5Ei%7D-%5Cfrac%7B%5Cpartial%5CGamma%5El_%7Bki%7D%7D%7B%5Cpartial+x%5Ej%7D%2B%5CGamma%5Em_%7Bkj%7D%5CGamma%5El_%7Bmi%7D%2B%5CGamma%5Em_%7Bki%7D%5CGamma%5El_%7Bmj%7D$

就是Riemann曲率

原文链接：https://blog.csdn.net/weixin_33585889/article/details/113038350