1. 问题描述:
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设 nums 只有一个重复的整数,找出这个重复的数 。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
示例 3:
输入:nums = [1,1]
输出:1
示例 4:
输入:nums = [1,1,2]
输出:1
提示:
2 <= n <= 3 * 10 ^ 4
nums.length == n + 1
1 <= nums[i] <= n
nums 中 只有一个整数出现两次或多次 ,其余整数均只出现一次
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/find-the-duplicate-number
2. 思路分析:
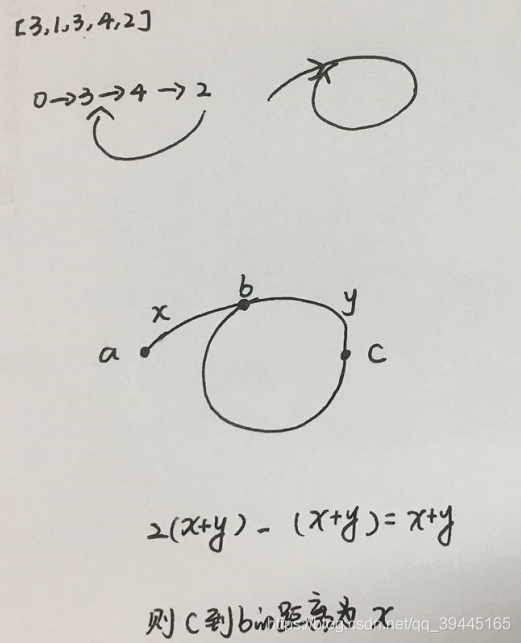
分析题目可以知道最容易想到的是使用哈希表对nums中出现的数字进行计数,因为使用是python语言所以可以使用collections.defaultdict(int)声明一个字典对nums中出现的数字进行计数,使用这个方法是最简单而且是比较高效的。除了这种方法之外,在y总的视频中讲到的是另外一个思路是寻找环的起点,感觉这种方法还是比较难想到的,其实我们可以将这些数字通过下标的方式连接起来,例如[3,1,3,4,2]可以表示为下图的形式,这样使用下标连接数字的时候那么相当于表示为链表的形式,从图中可以知道至少有两个起点指向的数字那么就是重复的数字,所以问题等价于寻找环的起点。寻找环的起点的经典方法是使用快慢指针a, b,慢指针每次走一步,快指针每次走两步这样因为存在环所以最终两个指针肯定会在一个位置相遇,假设两个指针相遇在下图中的c点,因为第一次相遇的时候快指针比慢指针肯定是多走一圈的,而且快指针比慢指针多走一倍的路程,所以根据这些关系我们得到图中c点到b点的长度为x,这样当两个指针相遇的时候我们令一个指针从最开始的位置走,另外一个指针从当前位置开始走,最终两个指针相等的位置就是环的起点。
3. 代码如下:
寻找环的起点:
from typing import List
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
a, b = 0, 0
while True:
# a指针每次走一步, b指针每一次走两步, 列表中两层嵌套表示的就是每次走两步的意思
a, b = nums[a], nums[nums[b]]
if a == b:
# a从开始位置走, b从当前位置开始走当两个位置系相等的时候说明是环的起点
a = 0
while a != b:
a = nums[a]
b = nums[b]
return a
return -1字典:
from typing import List
import collections
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
dic = collections.defaultdict(int)
for i in range(len(nums)):
if dic[nums[i]]:
return nums[i]
dic[nums[i]] += 1