#每日一题合集#牛客JZ34-JZ43

为了督促自己每天练一练编程
时间：2022年9月1日-2022年9月10日
网站：https://www.nowcoder.com/exam/oj/ta?tpId=13

9.1-JZ34. 二叉树中和为某一值的路径(二)

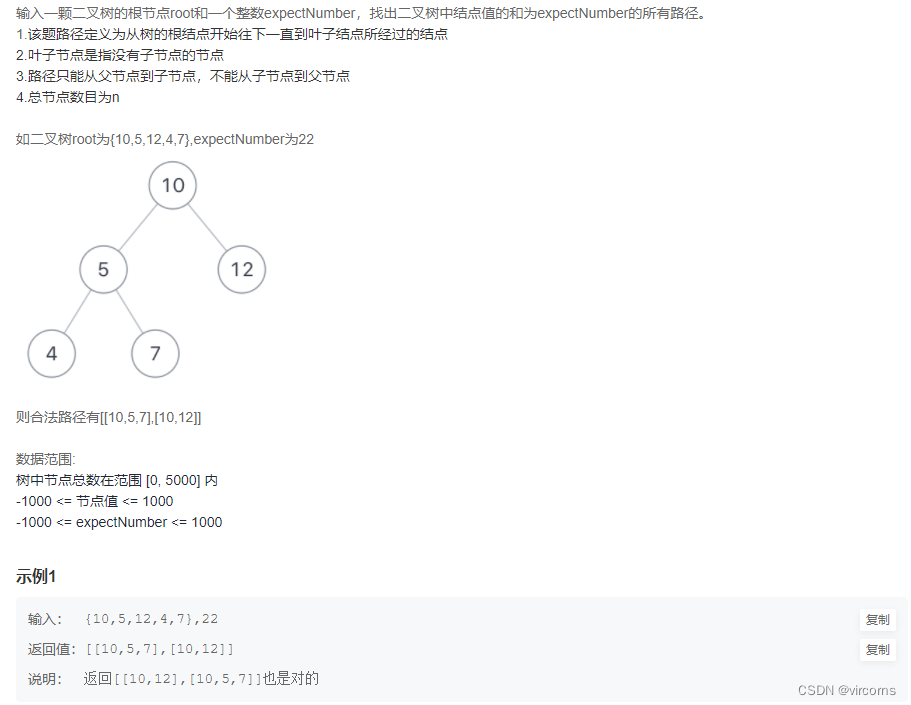
基础DFS。

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    void dfs(TreeNode* root,int n){
        if(root == NULL)
            return;
        path.push_back(root->val);
        n -= root->val;
        
        if(root->left == NULL && root->right==NULL && n == 0)
            res.push_back(path);
        
        dfs(root->left, n);
        dfs(root->right, n);
        path.pop_back();
        
    }
    vector<vector<int>> FindPath(TreeNode* root,int expectNumber) {
        dfs(root, expectNumber);
        return res;
    }
};

9.2-JZ35. 复杂链表的复制

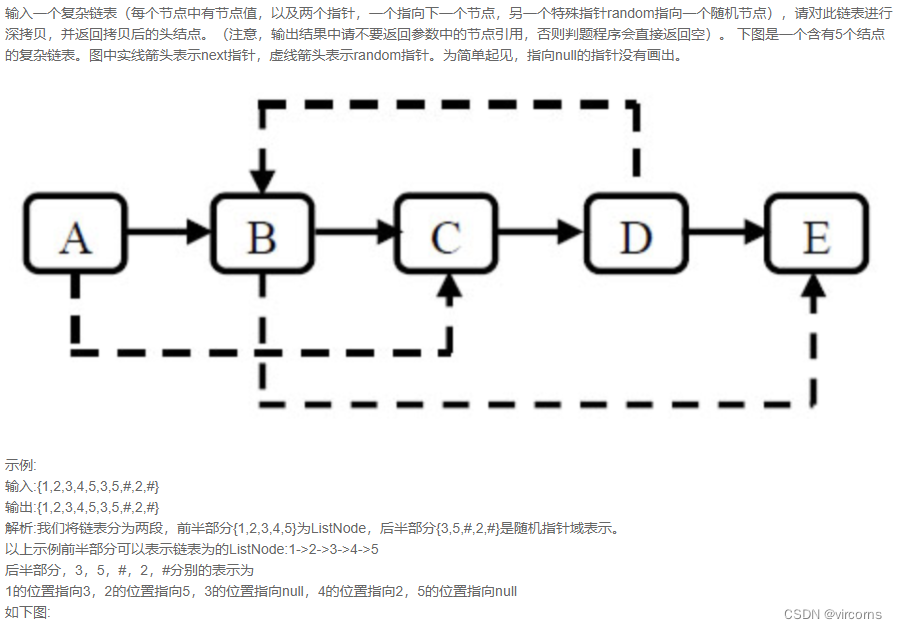
这个主要就难在“不能返回参数中的节点引用”。参考官方题解思路，直接在将拷贝后的每个节点插入到原始链表相应节点之后，这样连接random指针的时候，原始链表random指针后一个元素就是原始链表要找的随机节点，而该节点后一个就是它拷贝出来的新节点；拷贝结束后再拆分即可。

class Solution {
public:
    RandomListNode* Clone(RandomListNode* pHead) {
        if(pHead == NULL)
            return pHead;
        RandomListNode *cur = pHead;
        //step1：复制
        while(cur != NULL){
            RandomListNode *clone = new RandomListNode(cur->label);
            clone->next = cur->next;
            cur->next = clone;
            cur = clone->next;
        }
        //step2：random指针的拷贝
        cur = pHead;
        RandomListNode *clone = pHead->next;
        RandomListNode *res = pHead->next;
        
        while(cur != NULL){
            if(cur->random == NULL)
                clone->random = NULL;
            else
                clone->random = cur->random->next;
            
            cur = cur->next->next;
            if(clone->next != NULL)
                clone = clone->next->next;
        }
        
        //step3:拆分
        cur = pHead;
        clone = pHead->next;
        while(cur != NULL){
            cur->next = cur->next->next;
            cur = cur->next;
            
            if(clone->next != NULL)
                clone->next = clone->next->next;
            clone = clone->next;
        }
        return res;
    }
};

9.3-JZ36.二叉搜索树与双向链表

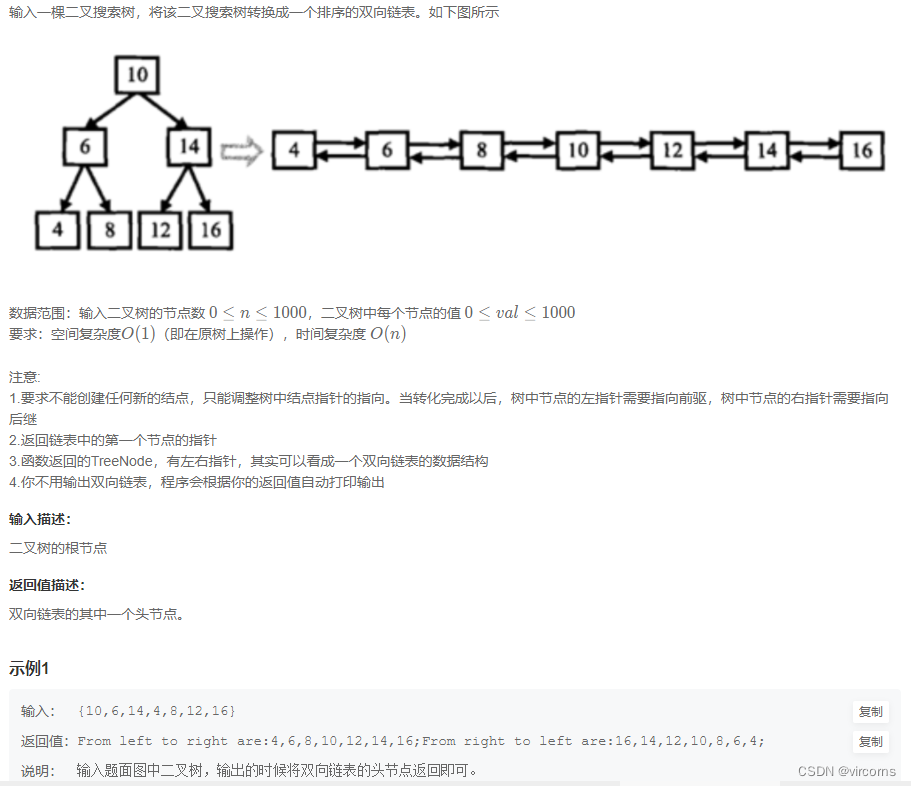
从给的图示就能看出来，是个中序遍历，和以往的中序的区别就是要考虑左右指针的指向。

class Solution {
public:
    TreeNode* head = NULL;
    TreeNode* pre = NULL;
    
    TreeNode* Convert(TreeNode* pRootOfTree) {
        if(pRootOfTree == NULL)
            return NULL;
        Convert(pRootOfTree->left);
        if(pre == NULL){
            head = pRootOfTree;
            pre = pRootOfTree;
        }
        else{
            pre->right = pRootOfTree;
            pRootOfTree->left = pre;
            pre = pRootOfTree;
        }
        Convert(pRootOfTree->right);
        return head;
    }
};

9.4-JZ37.序列化二叉树(未完成)

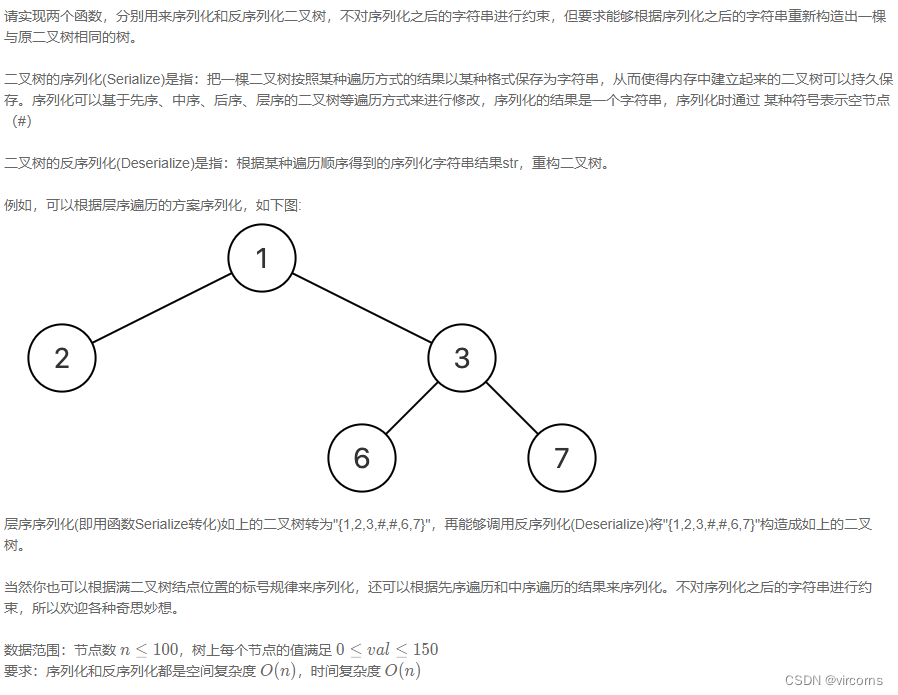
这个比较简单的就是前序遍历了，string转char这种也是参考了官方的题解。
但最后内存超限了，按着官方题解改也没想明白怎么回事

9.5-JZ38.字符串的排列

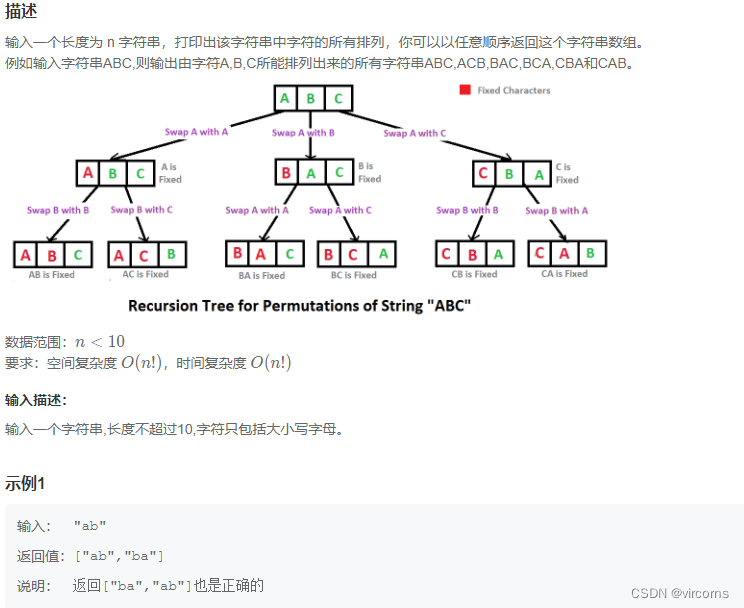
首先，我们需要一个数组记录哪些字符以及遍历过了，然后准备递归。递归的终止条件就是str里所有字符都用过了，也就是length相等；在每一个循环里，根据vis数组，已经加入的元素不能再次加入了；且如果当前的元素str[i]与同一层的前一个元素str[i-1]相同，也不能纳入。
将vis数组当前位置标记为使用过，然后进入下一层递归，进入回溯的时候需要再将vis=0，然后去掉刚才加入的字符。

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param str string字符串 
     * @return string字符串vector
     */
    void fun(vector<string> &res, string &str, string &tmp, vector<int> &vis){
        if(tmp.length() == str.length()){
            res.push_back(tmp);
            return;
        }
        for(int i = 0; i < str.length(); i++){
            if(vis[i])
                continue;;
            if(i > 0 && str[i] == str[i-1] && !vis[i-1])
                continue;;
            vis[i] = 1;
            tmp.push_back(str[i]);
            fun(res, str, tmp, vis);
            vis[i] = 0;
            tmp.pop_back();
        }
    }
    vector<string> Permutation(string str) {
        // write code here
        sort(str.begin(), str.end());
        vector<int> vis(str.size(), 0);
        vector<string> res;
        string tmp;
        
        fun(res, str, tmp, vis);
        return res;
    }
};

9.6-JZ39.数组中出现次数超过一半的数字

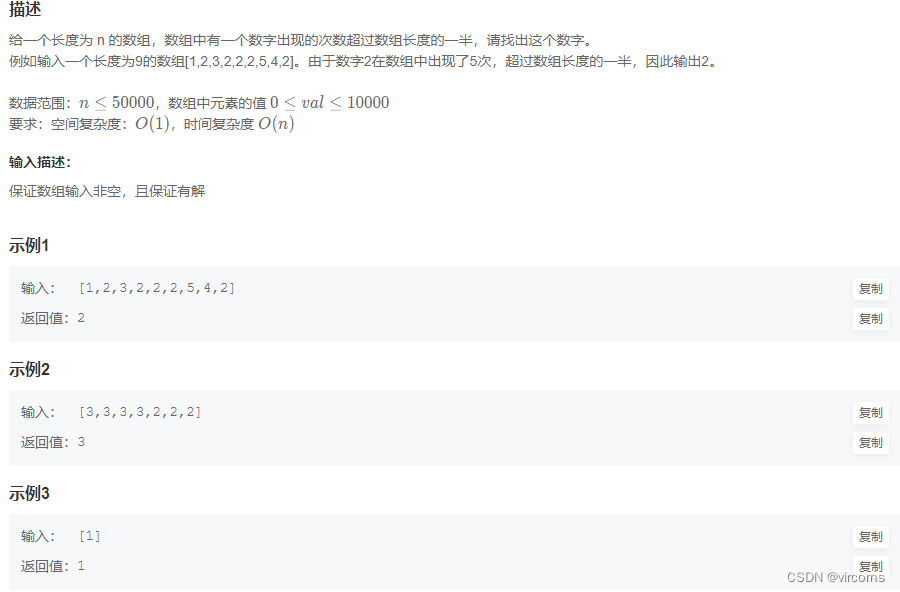
这个数出现次数超过一半，那他一定有一个是中位数，那么只需要判断中位数出现的次数即可。

class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        sort(numbers.begin(), numbers.end());
        int n = numbers.size();
        int center =  numbers[n/2];
        int cnt = 0;
        for(int i = 0; i < n; i++){
            if(center == numbers[i])
                cnt++;
        }
        if(cnt > n/2)
            return center;
        else
            return 0;
    }
};

9.7-JZ40. 最小的K个数

偷懒了偷懒了，看见第一反应就是sort就完事了，看了看别人的题解，可以堆排序、冒泡排序、自己实现快排等等

class Solution {
public:
    vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
        vector<int> res;
        if(k == 0 || k > input.size())
            return res;
        sort(input.begin(), input.end());
        return vector<int>{input.begin(), input.begin()+k};
    }
};

9.8-JZ41.数据流中的中位数

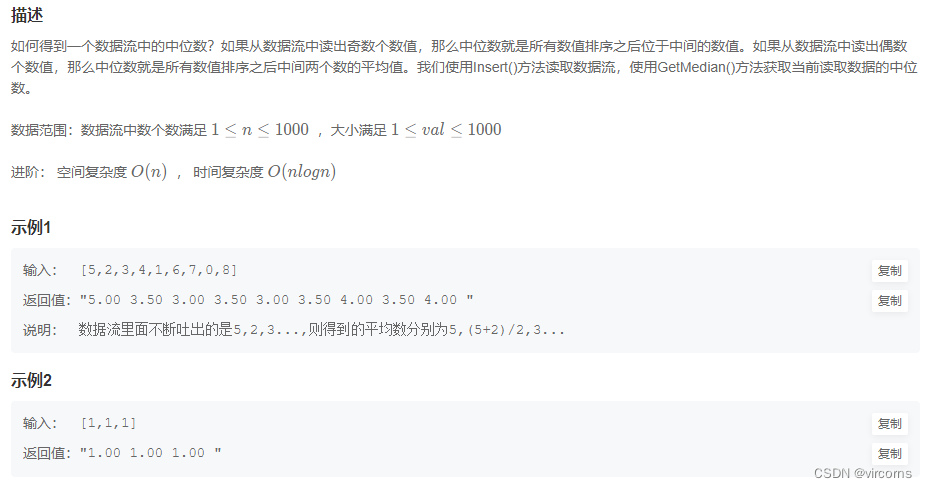
暴力就完了

class Solution {
public:
    vector<int> v;
    void Insert(int num) {
        v.push_back(num);
    }

    double GetMedian() { 
        sort(v.begin(),v.end());
        int n = v.size();
        if(n % 2 == 0){
            return 1.00*(v[n/2]+v[(n-1)/2])/2;
        }else{
            if(n == 1)
                return 1.00*v[n-1];
            return 1.00*v[n/2];
        }
    }
};

9.9-JZ42.连续子数组的最大和

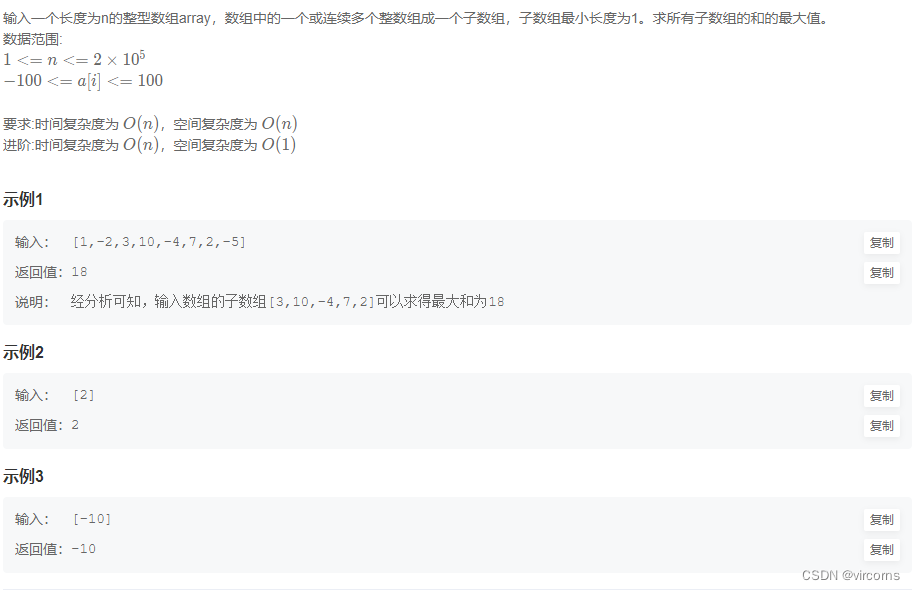
动态规划基础

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        int n = array.size();
        vector<int> dp(n, 0);
        dp[0] = array[0];
        int sum = dp[0];
        for(int i = 1; i < n; i++){
            dp[i] = max(dp[i-1]+array[i], array[i]);
            sum = max(sum, dp[i]);
        }
        return sum;
    }
};

9.10-JZ43.整数中1出现的次数（从1到n整数中1出现的次数）

class Solution {
public:
    int getsum(int n){
        int sum = 0;
        while(n){
            int tmp = n % 10;
            if(tmp == 1)
                sum++;
            n = n / 10;
        }
        return sum;
    }
    int NumberOf1Between1AndN_Solution(int n) {
        int sum = 0;
        for(int i = 1; i <= n; i++){
            sum += getsum(i);
        }
        return sum;
    
    }
};