前言

要成为绝世高手，并非一朝一夕，除非是天生武学奇才，但这种人…万中无一
-------包租婆

一、层序遍历是什么？

二叉树的层序遍历，就是从左到右一层一层的去遍历二叉树。需要借助队列这种数据结构来实现，队列先进先出，符合一层一层遍历的逻辑。而用栈先进后出模拟深度优先遍历也就是递归的逻辑。

二、实现方法(leetcode 102题为例)

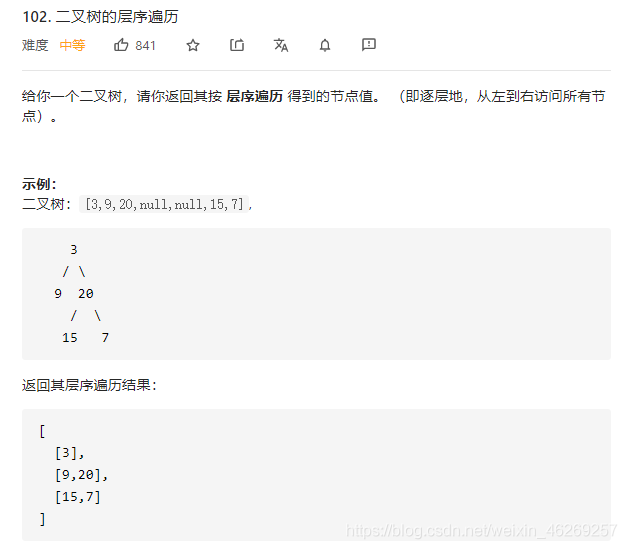
calss Solution{
public:
   //对比遍历结果输出就知道为什么返回值是vector容器嵌套了
   vector<vector<int>> levelOrder(TreeNode* root){
   queue<TreeNode*> que;//定义一个队列存放遍历结点的地址
   vector<vector<int>> res;//一个大vector数组[      ]
   
   if(root!=NULL) que.push(root);
  
   while(!que.empty()){
     int size=que.size();
     vec<int> vec;//一个小vector数组[]
    //这里一定要使用固定大小size,因为que.size()是不断变化的。
     for(int i=0;i<size;i++){
       TreeNode* node=que.front();
       que.pop();
       vec.push_back(node->val);
       if(node->left) que.push(node->left);
       if(node->right) que.push(node->right);
   }
   res.push_back(vec);//[[3],]
  }
  return res;
 }
 };
  
   

打怪升级1

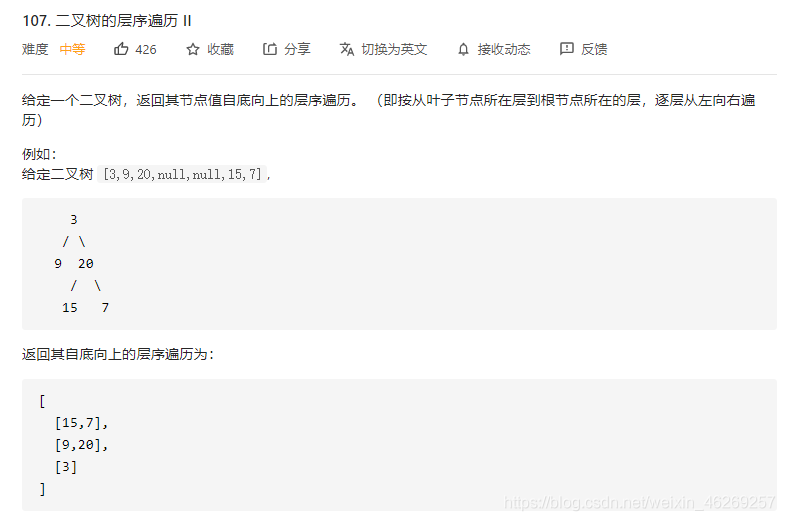
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {

    vector<vector<int>> res;
    queue<TreeNode*> que;
    if(root!=nullptr) que.push(root);

    while(!que.empty())//判断队列是否为空
    {
      int size=que.size();//不为空就计算一下队列元素的个数,便于确定将要入队元素个数
      vector<int> vec;
      
      for(int ii=0;ii<size;ii++)
      {
        TreeNode* node=que.front();//记录即将出队的元素地址
        que.pop();//元素出队

        vec.push_back(node->val);
        if(node->left) que.push(node->left);
        if(node->right) que.push(node->right);
      }
      
       res.push_back(vec);
    }
   
    reverse(res.begin(),res.end());//善于利用reverse算法，可大大提升效率

    return res;
    }
};

打怪升级2

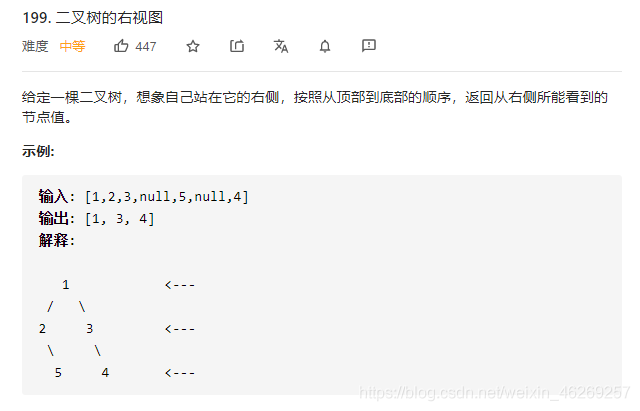
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
  
    vector<int> res;
    queue<TreeNode*> que;

    if(root!=nullptr) que.push(root);

    while(!que.empty())
    {
      int size=que.size();
      for(int ii=0;ii<size;ii++)
      {
        TreeNode* node=que.front();
        que.pop();

        if(ii==size-1) res.push_back(node->val);//判断是否遍历到单层的最后⾯的元素，如果是，就放进result数组中.
        if(node->left) que.push(node->left);
        if(node->right) que.push(node->right);
      }

    }
     return res;
    }
};

打怪升级3

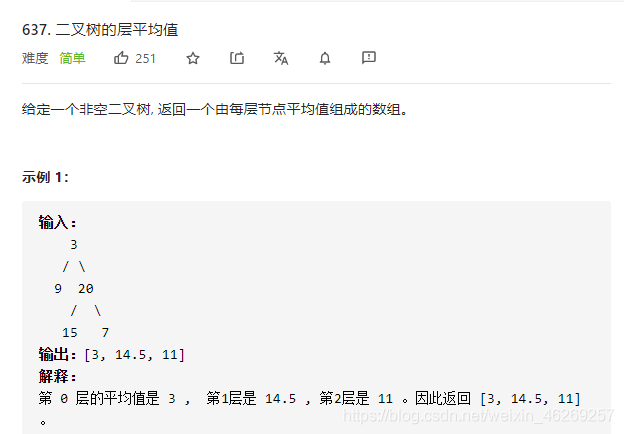
class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {

    vector<double> res;
    queue<TreeNode*>que;

    if(root!=nullptr) que.push(root);
    
    while(!que.empty())
    {
      int size=que.size();
      double sum=0;  //存放每一层的总和
      for(int ii=0;ii<size;ii++)
      {
        TreeNode* node=que.front();
        que.pop();
        sum=sum+(node->val);//统计每一层的总和
        if(node->left) que.push(node->left);
        if(node->right) que.push(node->right);
      }

      res.push_back(sum/size);//计算每一层的平均值

    }
   return res;
    }
};

打怪升级4

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    vector<vector<int>> levelOrder(Node* root) {
    
    vector<vector<int>> res;
    queue<Node*> que;

    if(root!=nullptr) que.push(root);

    while(!que.empty())
    {
      int size=que.size();
      vector<int> vec;

      for(int ii=0;ii<size;ii++)
      {
         Node* node=que.front();
         que.pop();
         vec.push_back(node->val);

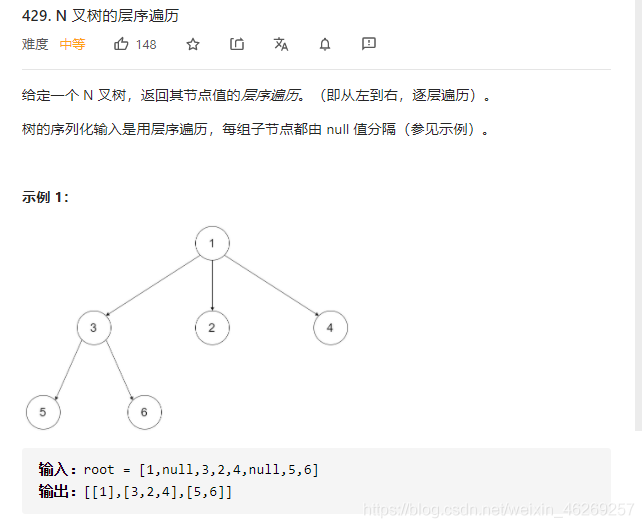
         for(int jj=0;jj<node->children.size();jj++)//注意结点定义
         {
           if(node->children[jj]) que.push(node->children[jj]);//每组子节点都由 null 值分隔，所以要判断结点里面指针为null的情况
         }
      }
      res.push_back(vec);
    }
     return res;
    }
};

打怪升级6

class Solution {
public:
    vector<int> largestValues(TreeNode* root) {

    vector<int> res;
    queue<TreeNode*> que;

    if(root!=nullptr) que.push(root);
    while(!que.empty())
    {
      int size=que.size();
      int maxnode=INT_MIN;//取整数最小值
      for(int ii=0;ii<size;ii++)
      {
       TreeNode* node=que.front();
       que.pop();
     
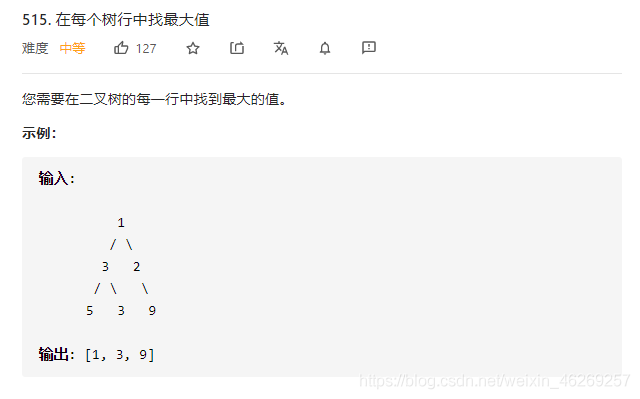
       if(node->val>maxnode) maxnode=node->val;//更新一行中的最大值
       if(node->left) que.push(node->left);
       if(node->right) que.push(node->right);
      }

      res.push_back(maxnode);

    } 
    return res;
    }
};

打怪升级7

//解法一
class Solution {
public:
    Node* connect(Node* root) {
     queue<Node*> que;

     if(root!=nullptr) que.push(root);
     while(!que.empty())
     {
       int size=que.size();

       for(int ii=0;ii<size;ii++)
       {
         Node* node=que.front();
         que.pop();
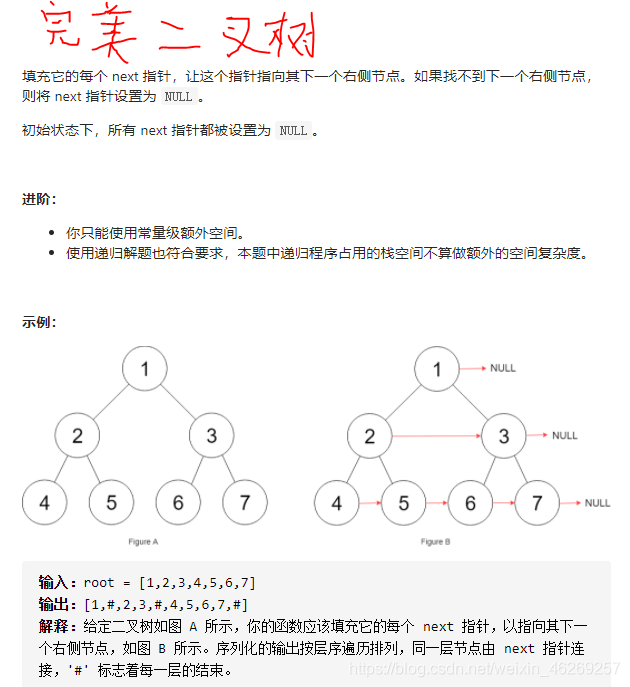
         if(ii!=size-1) node->next=que.front();

         if(node->left) que.push(node->left);
         if(node->right) que.push(node->right); 
       }
     }   
     return root;
    }
};

//解法二
class Solution {
public:
    Node* connect(Node* root) {
        queue<Node*> que;
        if (root != NULL) que.push(root);
        while (!que.empty()) {
            int size = que.size();
            Node* nodehead;
            Node* nodecur;
            for (int i = 0; i < size; i++) { // 开始每一层的遍历
                if (i == 0) {
                    nodehead = que.front(); // 记录一层的头结点
                    que.pop();
                    nodecur = nodehead;
                } else {
                    nodecur = que.front();
                    que.pop();
                    nodehead->next = nodecur; // 本层前一个节点next指向本节点
                    nodehead = nodehead->next;
                }
                if (nodecur->left) que.push(nodecur->left);
                if (nodecur->right) que.push(nodecur->right);
            }
           // nodePre->next = NULL; // 本层最后一个节点指向NULL
        }
        return root;
    }
};

打怪升级8

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
    queue<Node*> que;
    if(root!=nullptr) que.push(root);

    while(!que.empty()){
      int size=que.size();
      Node* nodehead;
      Node* nodecur;
  
      for(int ii=0;ii<size;ii++){
        if(ii==0)  {
          nodehead=que.front();
          que.pop();
          nodecur=nodehead;
        }
        else {
          nodecur=que.front();
          que.pop();
          nodehead->next=nodecur;
          nodehead=nodehead->next;
        }
        if(nodecur->left) que.push(nodecur->left);
        if(nodecur->right) que.push(nodecur->right);
      }
    }
    return root;
    }
};

总结

⼆叉树的层序遍历，就是图论中的⼴度优先搜索在⼆叉树中的应⽤，需要借助队列来实现。层序遍历遍历相对容易⼀些，只要掌握基本写法（也就是框架模板），剩下的就是在⼆叉树每⼀⾏遍历的时候做做逻辑修改。