1.题目描述
请计算n*m的棋盘格子(n为横向的格子数,m为竖向的格子数)沿着各自边缘线从左上角走到右下角,总共有多少种走法,要求不能走回头路,即:只能往右和往下走,不能往左和往上走。
2.思路分析
题目输入n为横向,m为竖向。同时,走的时候只能是往右往下走。
这里我们先看几个特殊情况:
1.n == 1 && m == 1,即只有一个格子的情况。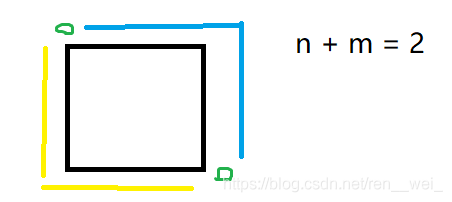
此时,满足要求的方案有两种,也就是n + m = 2。
2.当有一行多列格子。也就是n == 1 && m >= 1.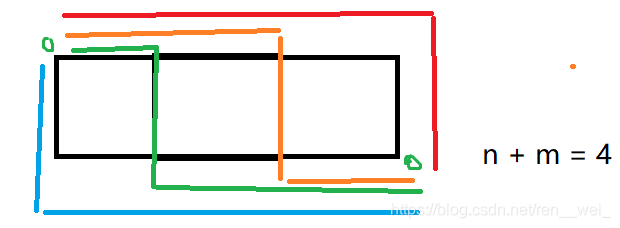
满足要求的也是n + m = 4种。
3.当有一列多行。也就是m == 1 && n >= 1.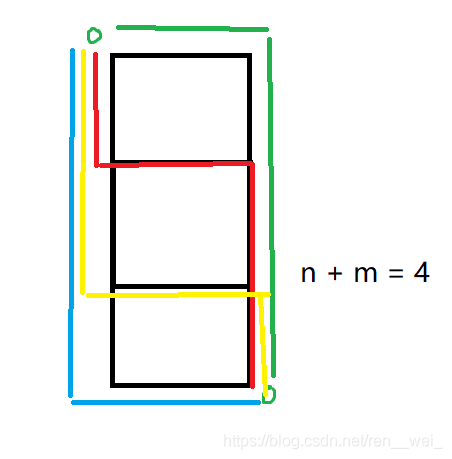
满足要求的也是n + m = 4种。
这是几种特殊的情况,我们发现,当只有一行或者一列时,满足要求的方案数就是n、m的和。
对于一般情况,我们再来分析: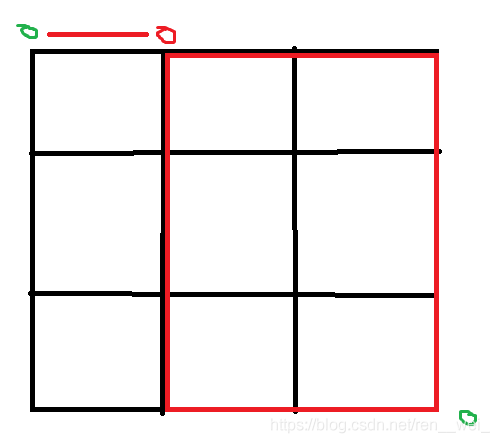
当朝右走一格的话,就只需要再求这个红框(n -1 , m)的方案数即可。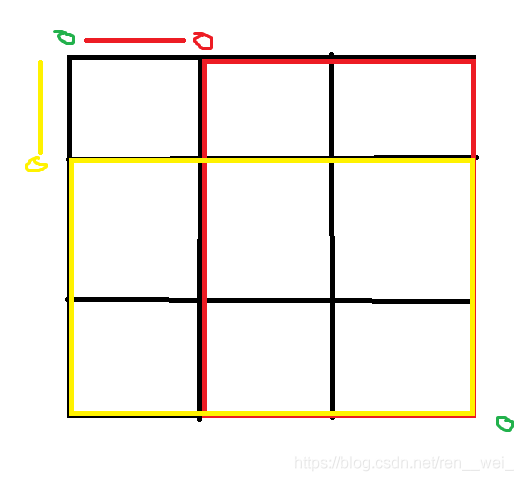
当朝下走一格的话,求出黄框(m - 1, n)的方案数即可。
然后将两种方案数加起来。
对于红框: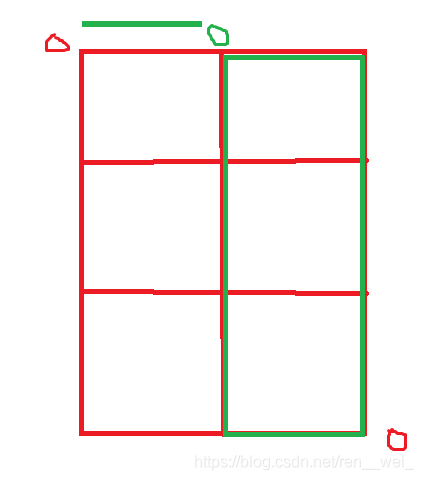
朝右走一格,就是求绿框(n - 1 - 1)的方案数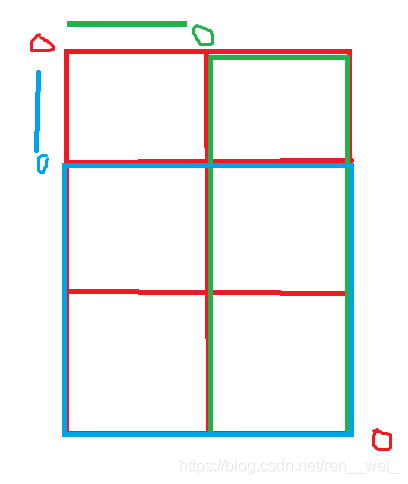
朝下走一格,就是求蓝框(n - 1, m - 1)的方案数。
然后将绿框和蓝框的方案数加起来就是红框的方案数。
对于黄框方案数的求法和红框是一样的,很明显,我们要用到递归。
对于一个一般的方格(n ,m),满足要求的方案数就是(n - 1, m)的方案数 + (m - 1, n)的方案数。
停止递归的条件就是,当n 或者 m为1 时。
那么我们的分析就结束了,下面是代码:
3.代码
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
int n = sc.nextInt();
int m = sc.nextInt();
System.out.println(med(n, m));
}
}
public static int med(int n, int m){
if((n == 1 && m >= 1) || (m == 1 &&n >= 1)){
return m + n;
}
return med(n - 1, m) + med(n, m - 1);
}
}
版权声明:本文为ren__wei_原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。