0x00 背景
最近在做毕设,需要使用Google的word2vec。查阅了相关资料,总结后,写下这篇。
注,本文大多取自以下内容:
cbow例子,取自知乎,已取得答主同意
word2vec数学原理详解
word2vec今生前世
0X01 简介
word2vec是Google与2013年开源推出的一个用于获取word vecter的工具包,利用神经网络为单词寻找一个连续向量看空间中的表示。
word2vec有两种网络模型,分别为:
- Continous Bag of Words Model (CBOW)
- Skip-Gram Model
在开始之前,需要一些准备知识(统计语言模型):- 《word2vec的前世今生》
http://www.cnblogs.com/iloveai/p/word2vec.html- 吴军博士的《数学之美》
0X02 CBOW网络模型
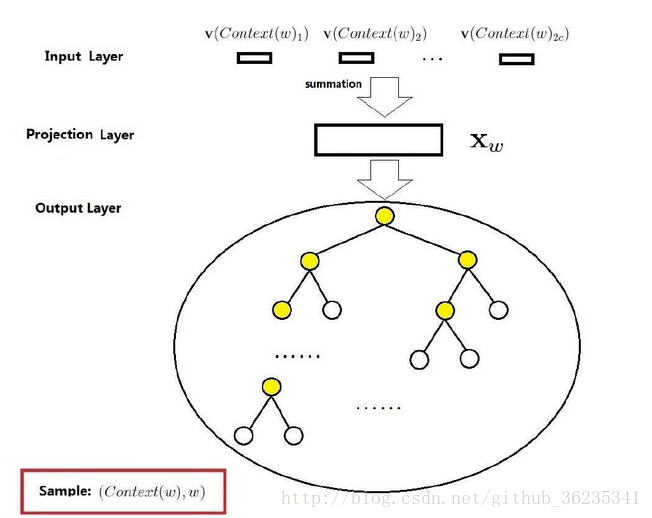
- 输入层:
假设当前词为W,Context(W)由W前后C个词构成。
所以输入层中有2c个词向量, v(Context(W)1), ······,v(Context(W)2c)
- 投影层:
将输入层的2c个向量累加,即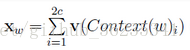
- 输出层:
输出层为一棵二叉树,以词库中的词作为叶子结点,并以词频为权重构造出来的Huffman树,如果词库中有D个词,则有D个叶子结点。
0X03 CBOW模型流程举例
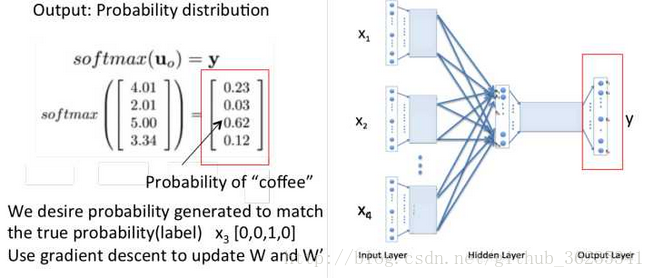
假设 Courpus = { I drik coffee everyday } ,根据 “I”“drink”“everyday”来预测“coffee”。
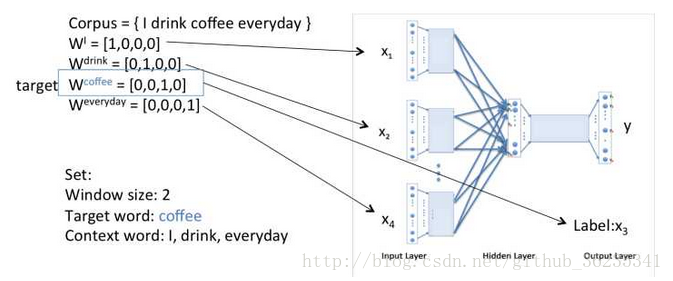
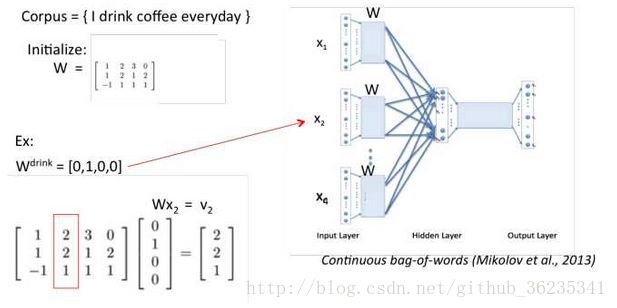
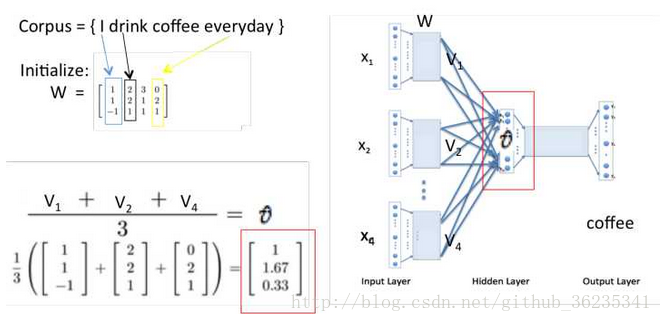
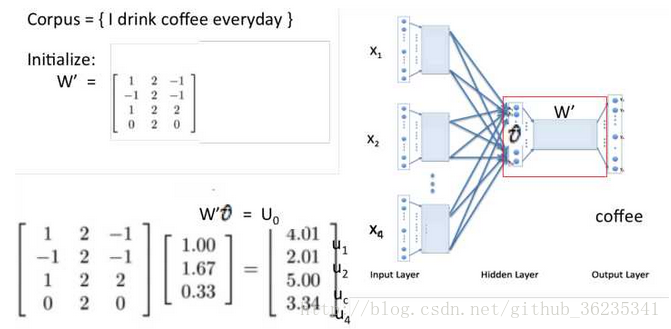
投影层将每个词向量加起来,
这里Xw即上图Uo ,当Xw传导到输出层时,因为输出层为一棵二叉树,每一次分支都可视为进行一次二分类,将分到左边为负类,分到右边为正类。
根据sigmoid函数,可将二分类函数写成: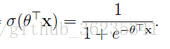
所以,一个结点被分到正类的概率是: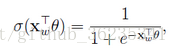
被分到负类的概率是: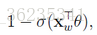
这里Θ向量是待定参数。
将每个分支的概率相乘就是所需的 P( W | Context(W) )
对概率函数取对数,即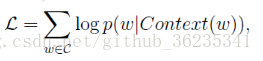
并对式子求 Xw的偏导 和 Θ 的偏导。
详细过程在《word2vec中的数学原理详解》http://suanfazu.com/t/word2vec-zhong-de-shu-xue-yuan-li-xiang-jie-duo-tu-wifixia-yue-du/178
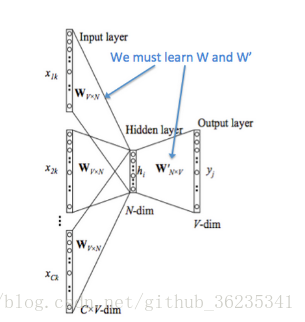
最终,通过大量的数据迭代,使用梯度下降更新W和W’,来最小化loss函数,训练结束后的W就是词向量的矩阵,任何一个单词的One-Hot表示乘以这个矩阵W就可以得到其词向量的表示。
0X04 word2vec的使用
我用的是python的gensim库
from gensim.models.word2vec import Word2vec model = Word2Vec(data_set,size,window,negative,iter) model.save(file) // 训练完后保存 model = Word2Vec.load(file) model.wv['compute'] // 词向量保存在wv实例里,得到“compute”的词向量 model.wv.similarity('woman', 'man') // 求词与词之间的相关性几个重要的参数:
sg : 为0则cbow(默认),为1则Skip-gram
size:特征向量的维度
window:预测词与当前词的最大距离
negative:if > 0 ,使用负样本,通常5-20,默认5个噪声词
iter:词库的迭代次数当然了,想了解更多可以上官网看看。
附上链接
https://radimrehurek.com/gensim/models/word2vec.html