线性回归预测糖尿病

[Python数据挖掘课程] 五.线性回归知识及预测糖尿病实例
 数据集介绍
 常见的sklearn数据集
 常用数据集
 斯坦福公开课：第二课单变量线性回归

预测房价，也就是求取模型参数，当前自变量(输入特征)是房子面积x，因变量是房价y.给定了一批训练集数据。我们要利用手上的训练集数据，得出x与y之间的函数f关系，并用f函数来预测任意面积x对应的房价。

假设x与y是线性关系，则我们可以接着假设一元线性回归函数如下来代表y的预测值：
$h_{\theta}(x)=\theta_{\mathrm{0}}+\theta_{1} x$

如何利用现有的训练集来判定未知参数 $(\theta_{\mathrm{0}},\theta_{1})$ 的值，使其让h的值更接近实际值y? 训练集指的是已知x,y值的数据集合。
一种方法是计算它的成本函数(Cost function)，即预测出来的h的值与实际值y之间的方差的大小来决定当前的 $(\theta_{\mathrm{0}},\theta_{1})$ 值是否是最优的！
常用的成本函数(Cost function)是最小二乘法求解残差平方和：
$J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}$

求解方法：梯度下降（Gradient descent）

1.载入并查看数据

from sklearn import datasets

diabets = datasets.load_diabetes()

print(diabets.data)  # 数据
print(diabets.target)  # 类标
print('总行数：', len(diabets.data), len(diabets.target))  # target为预测指标
print('特征数：', len(diabets.data[0]))   # 每行数据集维数
print('数据类型', diabets.data.shape)
print('总行数：', type(diabets.data), type(diabets.target))

2.完整代码

from sklearn import datasets
from sklearn import linear_model
import matplotlib.pyplot as plt
import numpy as np

#数据集划分
diabetes = datasets.load_diabetes()                #载入数据
diabetes_x_temp = diabetes.data[:, np.newaxis, 2]  #获取一个特征
diabetes_x_train = diabetes_x_temp[:-20]           #训练样本,从0到-20行（不包含最后20行）
diabetes_x_test = diabetes_x_temp[-20:]            #测试样本 后20行
diabetes_y_train = diabetes.target[:-20]           #训练标记
diabetes_y_test = diabetes.target[-20:]            #预测对比标记


#回归训练及预测
clf = linear_model.LinearRegression()
clf.fit(diabetes_x_train, diabetes_y_train)  #注: 训练数据集


#系数 残差平法和 方差得分
print('Coefficients :\n', clf.coef_)
print("Residual sum of square: %.2f" % np.mean((clf.predict(diabetes_x_test) - diabetes_y_test) ** 2))
print("variance score: %.2f" % clf.score(diabetes_x_test, diabetes_y_test))


#绘图
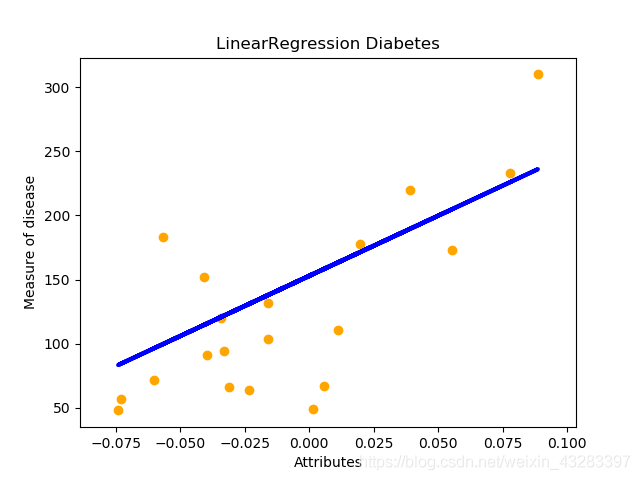
plt.title('LinearRegression Diabetes')   #标题
plt.xlabel(u'Attributes')                 #x轴坐标
plt.ylabel(u'Measure of disease')         #y轴坐标


#点的准确位置
plt.scatter(diabetes_x_test, diabetes_y_test, color = 'orange')


#预测结果 直线表示
plt.plot(diabetes_x_test, clf.predict(diabetes_x_test), color='blue', linewidth = 3)
plt.show()

结果为：

Coefficients :
 [938.23786125]
Residual sum of square: 2548.07
variance score: 0.47

在这里插入图片描述

3.代码优化
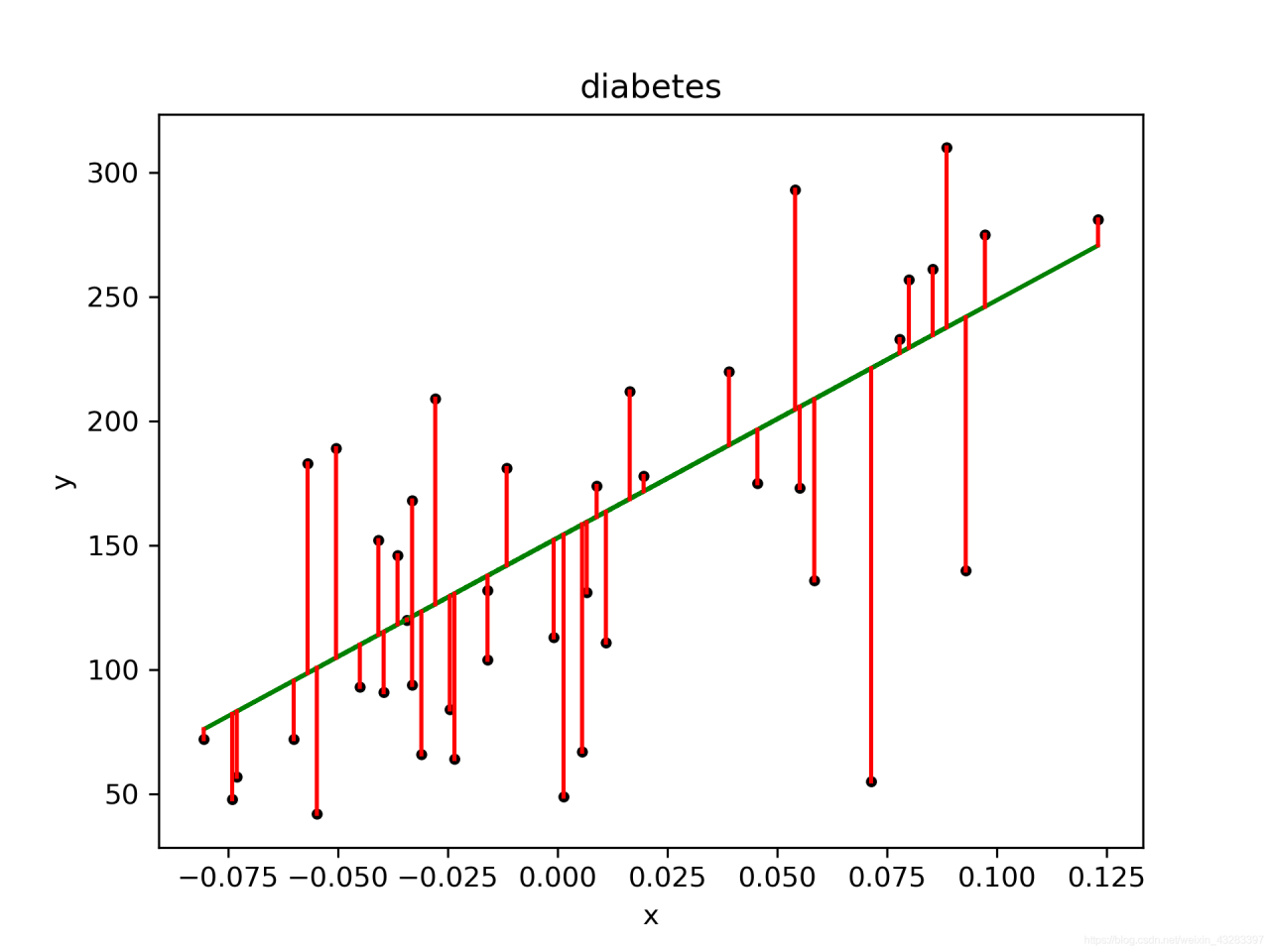
优化后的代码，增加了斜率、截距的计算，同时增加了点图到线性方程的距离，保存图片设置像素。

#第一步 数据集划分
from sklearn import datasets
import numpy as np


#获取数据 10*442
d = datasets.load_diabetes()  # 数据10*442
x = d.data
print(u'获取x特征')
print(len(x), x.shape)
print(x[:4])


#获取一个特征 第3列数据
x_one = x[:,np.newaxis, 2]
print(x_one[:4])


#获取的正确结果
y = d.target
print(u'获取的结果')
print(y[:4])

#x特征划分
x_train = x_one[:-42]                   # 训练集X[0:400]
x_test = x_one[-42:]                    # 预测集X[401:442]
print(len(x_train), len(x_test))
y_train = y[:-42]                       # 训练集Y[0:400]
y_test = y[-42:]                        # 预测集Y[401:442]
print(len(y_train), len(y_test))


#第二步 线性回归实现
from sklearn import linear_model
clf = linear_model.LinearRegression()
print(clf)
clf.fit(x_train, y_train)
pre = clf.predict(x_test)
print(u'预测结果')
print(pre)
print(u'真实结果')
print(y_test)


#第三步 评价结果
cost = np.mean(y_test-pre)**2
print(u'平方和计算:', cost)
print(u'系数', clf.coef_)
print(u'截距', clf.intercept_)
print(u'方差', clf.score(x_test, y_test))


#第四步 绘图
import matplotlib.pyplot as plt
plt.title("diabetes")
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x_test, y_test, 'k.')
plt.plot(x_test, pre, 'g-')

for idx, m in enumerate(x_test):
    plt.plot([m, m],[y_test[idx],
              pre[idx]], 'r-')

plt.savefig('power.png', dpi=300)

plt.show()

获取x特征
442 (442, 10)
[[ 0.03807591  0.05068012  0.06169621  0.02187235 -0.0442235  -0.03482076
  -0.04340085 -0.00259226  0.01990842 -0.01764613]
 [-0.00188202 -0.04464164 -0.05147406 -0.02632783 -0.00844872 -0.01916334
   0.07441156 -0.03949338 -0.06832974 -0.09220405]
 [ 0.08529891  0.05068012  0.04445121 -0.00567061 -0.04559945 -0.03419447
  -0.03235593 -0.00259226  0.00286377 -0.02593034]
 [-0.08906294 -0.04464164 -0.01159501 -0.03665645  0.01219057  0.02499059
  -0.03603757  0.03430886  0.02269202 -0.00936191]]
[[ 0.06169621]
 [-0.05147406]
 [ 0.04445121]
 [-0.01159501]]
获取的结果
[151.  75. 141. 206.]
400 42
400 42
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
预测结果
[196.51241167 109.98667708 121.31742804 245.95568858 204.75295782
 270.67732703  75.99442421 241.8354155  104.83633574 141.91879342
 126.46776938 208.8732309  234.62493762 152.21947611 159.42995399
 161.49009053 229.47459628 221.23405012 129.55797419 100.71606266
 118.22722323 168.70056841 227.41445974 115.13701842 163.55022706
 114.10695016 120.28735977 158.39988572 237.71514243 121.31742804
  98.65592612 123.37756458 205.78302609  95.56572131 154.27961264
 130.58804246  82.17483382 171.79077322 137.79852034 137.79852034
 190.33200206  83.20490209]
真实结果
[175.  93. 168. 275. 293. 281.  72. 140. 189. 181. 209. 136. 261. 113.
 131. 174. 257.  55.  84.  42. 146. 212. 233.  91. 111. 152. 120.  67.
 310.  94. 183.  66. 173.  72.  49.  64.  48. 178. 104. 132. 220.  57.]
平方和计算: 83.19234082703763
系数 [955.70303385]
截距 153.00018395675963
方差 0.42720426706720194

在这里插入图片描述

原文链接：https://blog.csdn.net/weixin_43283397/article/details/103141669