第二部分
第15题
因为集合M不是空集,所以M∩N=φ需要分N是空集和N不是空集两种情况讨论。
附不等式“k+3<-1或6-k≥2”的求解过程:得k<-4或k≤4,“或”就是求并集,并集是k≤4(如果不明白,画数轴求并集),所以这个不等式的解集为k≤4。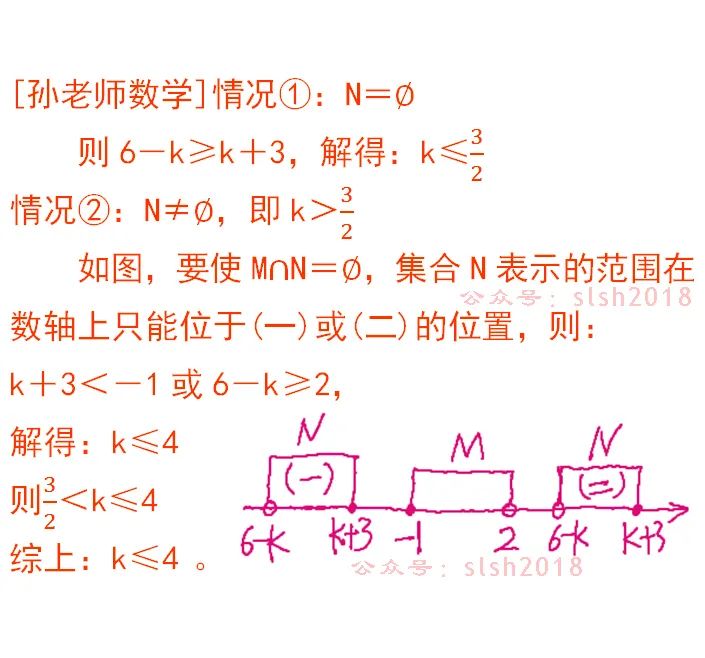

R是实数集,集合A中的元素是一元二次方程的解,则A∩R=φ说明A是空集,即一元二次方程无解,则其判别式△<0;又m在根号下,所以m必须≥0。


因为集合B不是空集,所以A∩B=φ要分两种情况进行讨论:A是空集和A不是空集。
A是空集时,集合A中的一元二次方程无解,则判别式△<0。见第一条虚线上方。
A不是空集时,一元二次方程有解,则必有△≥0;因为集合B中的元素是大于0的实数,要使A∩B=φ,一元二次方程的两个解必须都≤0,则只需两根之和≤0,且两根之积≥0;所以情况②共3个限制条件。见两条虚线中间部分。
情况①和情况②中m取值范围的并集就是最终m的取值范围。 第18题
因为A∩B≠φ,所以A和B都不能是空集,已知B不是空集,则集合A也不能是空集。见第一条虚线上方。
在A不是空集的条件之下,集合A和B中不能有公共元素,故必须如图所示。见两条虚线中间部分。
a≤1和a<2的交集就是最终a的取值范围。
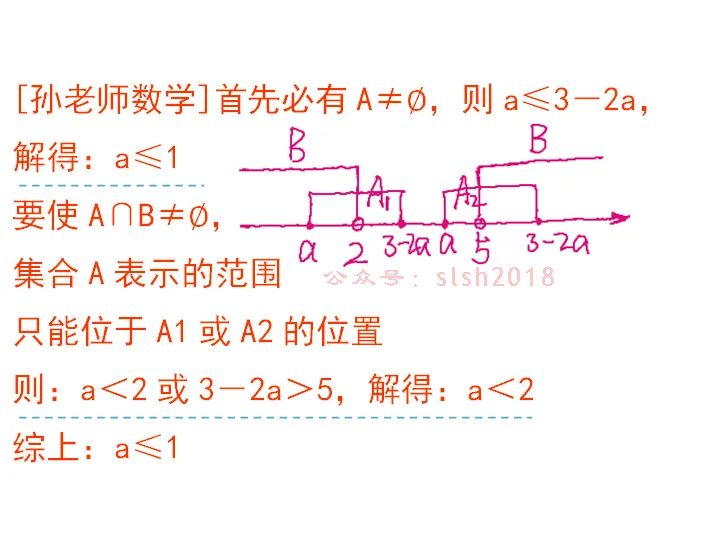

A∩B≠φ,说明集合A和B中有公共元素;集合B中有两个元素:a和4,因为4的平方不≤1,所以4不在A中,则a必须在集合A中,则a的平方≤1。


A∪B=R,意思是:集合A表示的范围和集合B表示的范围,合在一起可以包含整个数轴。
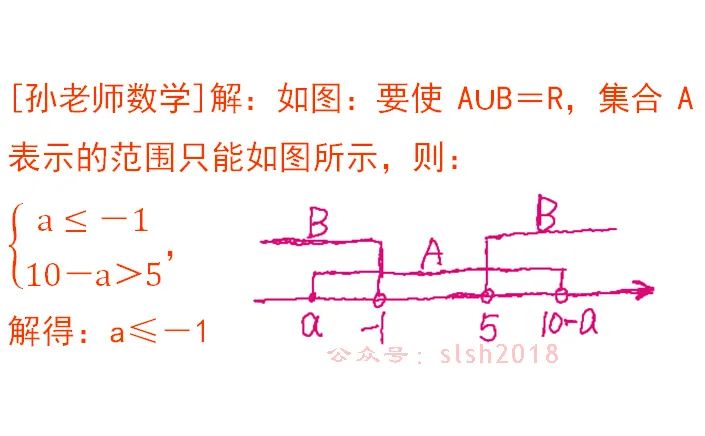

因为B不是空集,A可以是空集,所以A∩B=φ要分两种情况进行讨论:A是空集和A不是空集。
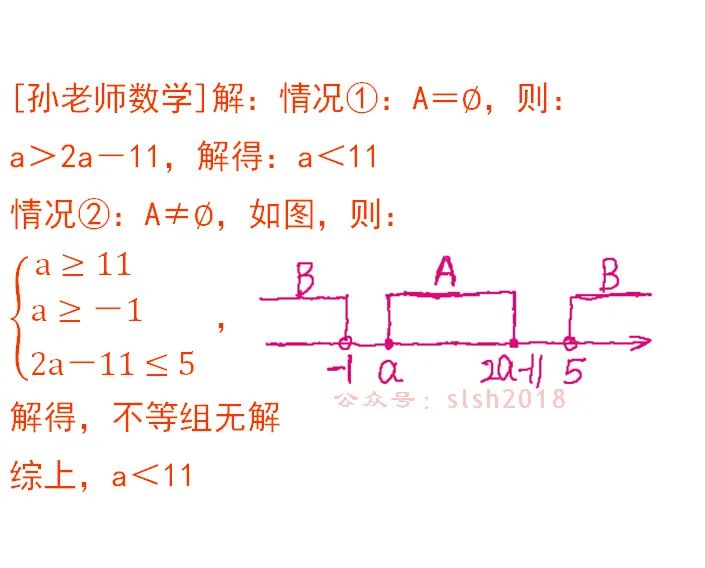

解答过程:
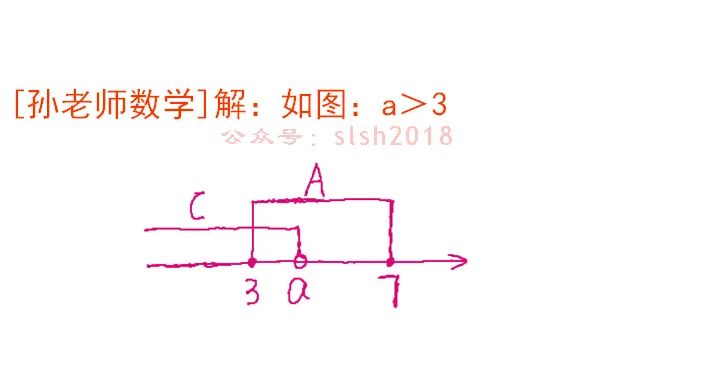

A∩B≠φ,说明集合A和B中有公共元素,集合B中有两个元素2a和4,则这两个元素中至少有一个在集合A中。


A∩B=B说明B包含于A,又B可以是空集,所以要分两种情况进行讨论:B是空集和B不是空集。B是空集时,B中的一元二次方程无解,如下。

B不是空集时,B中的一元二次方程有解,要使B包含于A,集合B中的一元二次方程的解只能是1或2,所以又要分两种情况进行讨论,如下。

为什么求出a的值之后,要带入集合验证B是否包含于A?因为一元二次方程有2个解,1是方程的解,不能保证暂时未知的另一个解也在集合A中(即另一个解是1或2),所以要验证。
第25题
存在性问题,如果能够求出满足题意的x的值,就存在,否在就是不存在。
CsA={0},说明0在全集S中,且不在A中,由此可得如下的不等式组。

温馨提醒:公众号菜单处有分好类的课程和专题。