R 加权最小二乘 代码_R语言基础及稳健回归实现

注：本文是王桢罡对“R语言基础及稳健回归实现”的介绍

R语言简介

R是统计领域广泛使用的诞生于1980年左右的S语言的一个分支。R是一套由数据操作、计算和图形展示功能整合而成的套件。包括：有效的数据存储和处理功能，一套完整的数组(特别是矩阵)计算操作符，拥有完整体系的数据分析工具，为数据分析和显示提供的强大图形功能，一套(源自S语言)完善、简单、有效的编程语言(包括条件、循环、自定义函数、输入输出功能)。常被用于统计分析，是一种极具分享精神的语言环境！

两种稳健回归方法(Huber损失和Bisquare损失的M估计)

稳健回归

稳健回归(robust regression)是统计学稳健估计中的一种方法，其主要思路是将对异常值十分敏感的经典最小二乘回归中的目标函数进行修改。经典最小二乘回归以使误差平方和达到最小为其目标函数。因为方差为一不稳健统计量，故最小二乘回归是一种不稳健的方法。不同的目标函数定义了不同的稳健回归方法。常见的稳健回归方法有：最小中位平方(least median square；LMS)法、M估计法等。

M估计

M 估计是基于最小二乘估计发展起来的一种抗差估计(Robust Estimation)方法。它实质上包含了最小二乘估计和很多稳健估计方法的一种广义类。其思想就是通过最小化损失函数的方法来估计参数。不同的方法选择不同的损失函数来达到不同的稳健效果。

  • Huber损失
cfb585e557c4d46c1b1d065970293b33.png

上式给出了Huber损失的函数表达式，其中δ是事先给定的，常用值为1.345。y代表真实值，f(x)表示拟合值。

5273d5862fb0377b64f52cd5a418ad36.png

可以看出，当一个点的真实值远离群体时，它与其拟合值就越远，但这种“远”所带来的损失的增长速度是比较慢的(此处的比较慢，是相对于最小二乘而言的)。所以这种损失函数，实际上控制了离群点的权重，使得它的影响力没有那么高，最终达到稳健的效果。

  • Bisquare损失(也称Biweights)
a787e22d9edb3ff15933b3040c5dc23d.png

上式给出了Bisquare损失的函数表达式，其中c是事先给定的，常用值为4.685，c决定了函数的拐点。r就是真实值和拟合值的差。

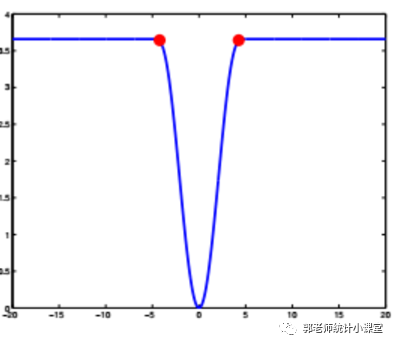
6eef54c1d07f1f195830fd6b178b6f4f.png

可以看出，这种损失函数对离群点更加“干脆”和“残忍”，在离群点“远”到一定程度之后，它的损失就成为一个常数，不管这个点多么“离谱”，它对估计的影响也不会再变化了。这种损失函数最终会导致一些特别偏离的野点的权重下降到很小，趋近于0，也能达到稳健的效果。

R基础代码和两种稳健方法的实现

本文需要使用MASS包

#R语言超级基础分享会
#(两种稳健回归方法的随机模拟实现)

#导入包
library(MASS)
#查看整个包的帮助文档
help(package = "MASS") 
#查看某个函数的帮助文档
?c#把圆括号里的用逗号分隔的元素，整合成一个向量。

#创建数据集和引用其中的元素
#标量
data_scalar1 1
data_scalar2 = "one"  
data_scalar3 TRUE

一定要注意

length(testdata 1:10)
#length(testdata_1 = 1:5) #此行代码是错误示范
#
testdata_2 = 1:5
length(testdata_2)#向量，元素必须为同一类型
data_vector1 1,2,3,4,5,6)
data_vector2 "one","two","three")
data_vector3 TRUE,TRUE,FALSE)
data_vector4 1:6)
data_vector5 0,100)
data_vector6 1,5,0.5)
data_vector6
data_vector2[1] #序号为1的元素即为第一项
data_vector2[-1] #不显示第一项
data_vector2[c(-1,-2)]

#矩阵，元素必须为同一类型
data_matrix1 2,3)
data_matrix2 2,3,byrow = TRUE)
data_matrix1
data_matrix2
data_matrix1[1,2] #引用第一行第二列的元素
data_matrix1[-1,] #得到除去第一行的矩阵
data_matrix1[1,-1]
data_matrix1[1:2,c(1,3)]

#数据框，每一列元素性质可以不同
frame1 1:3,c("one","two","three"),fix.empty.names = FALSE)
frame1

#模拟随机生成数据
x 4,15,0.5)
e 23,mean = 0,sd = 1) #生成23个服从N(0,1)的随机数
y 0.5*x+0.3+e
y[14] 20   #加入异常值，x=10.5时，y设为20

runif(10,min = 0,max = 1) #均匀分布随机数
rpois(10,lambda = 2) #泊松分布随机数
sample(1:5,size = 3,replace = TRUE,prob = c())#TRUE代表有放回
rcauchy(10,0,1) #柯西分布随机数

现在表格文件大多都是.xlsx格式了，使用.csv和.txt格式的表格不常见了。所以推荐安装xlsx包，但此包需要安装JAVA和JDK，请读者自行安装。

#library(xlsx)
#mydata #write.xlsx(mydata,"F:/mydata.xlsx") #注意正反斜杠#从EXCEL中导入数据#library(readxl)#dataset1 #col_types = c("skip",  "numeric", "numeric"))#View(dataset1)
dataset1 #绘制简单图
plot(dataset1,type = "o", main = "一张图",
     sub = "统计学院", xlab = "我的自变量",
     ylab = "我的因变量", lty = 1, pch = 5,
     col = "red",fg="blue",col.axis = "blue",
     font = 2,xlim = c(),ylim = c())
axis(side = 1,at = 10.5 ,label = "out",col = "red")
legend(x=4,y=20,c("图例1","图例2"))
abline(a=0.3,b=0.5) #在图上添加一条截距为a，斜率为b的直线
abline(v=10.5,lty = 5) #在x=10.5初，画一条垂直于x轴的线
text(x=12,y=20,")

layout这个函数中需要构造一个矩阵，第i张图占据矩阵中值为i的所有元素所在的位置。


layout(matrix(c(1,1,2,3),2,2,byrow = TRUE)) #利用矩阵在一个平面上布局多图
plot(dataset1,type = "l")
plot(dataset1,type = "o")
plot(dataset1,type = "h")
layout(matrix(c(1),1,1))

#重复和循环
#for循环
for (i in 1:9) {  #圆括号中的参数用于控制循环次数，也可以引用
  print(i+1)
}

#while循环
j=0
while (j<5 | j<3) {  #R语言中的“或”。
  print(j)
  j 1
}

j=0
while (j<5 & j<3) {  #R语言中的“与”。
  print(j)
  j 1
}

j=0
while (j != 4) {  #R语言中的“非”。
  print(j)
  j 1
}

注意|和||，&和&&的区别。

testbool TRUE,FALSE,FALSE)
testbool_1 TRUE,TRUE,FALSE)
#都是或，但两杠仅比较第一分量，一杠各个分量都比且输出为向量
testbool | testbool_1  
testbool || testbool_1 
#都是与，差别同上
testbool & testbool_1
testbool && testbool_1

#if-else条件执行
if(5) print("统计学院真的很棒！") #R语言中非零的数在逻辑运算中都被认为是TRUE
if(0) print("R语言真的很棒！")
if(-3) print("华为加油！")

year = 2021
if(year == 2020){
  print("2020年可真难啊")
}else if(year == 2019){
  print("2019年还是不错的")
}else if(year == 2021){
  print("希望2021年能好起来")
}

ifelse(x1:10 5,print("睡觉"),print("醒了"))

j=0
while(1){
  sq 2
  print(sq)
  if(sq == 49) break #满足条件则跳出整个循环
  j 1
}
print(paste(j,"的平方是49"))

for (j in 1:5) {
  if(j == 3){
    next  #满足条件则跳出此次循环
  }
  print(j)
}

#一元回归模型
?lm
View(dataset1)
mymodel summary(mymodel)

mymodel$fitted.value

plot(dataset1,type = "o", main = "一张图",
     sub = "统计学院", xlab = "我的自变量",
     ylab = "我的因变量", lty = 1, pch = 5,
     col = "red",fg="blue",col.axis = "blue",
     font = 2,xlim = c(),ylim = c())
axis(side = 1,at = 10.5 ,label = "out",col = "red")
legend(x=4,y=20,c("图例1","图例2"))
abline(a=0。3,b=0.5) #在图上添加一条截距为a，斜率为b的直线
abline(v=10.5,lty = 5)
text(x=12,y=20,")
abline(mymodel,col = "green")

rlm函数，默认使用Huber损失，可通过参数psi来选择其他损失函数。


#一元稳健回归模型
?rlm
#M估计

#方法一：Huber损失
mymodel_huber abline(mymodel_huber,col = "blue")
#查看残差大的离群点权重是不是低
w_huber w_huber

#方法二：Bisquare损失
mymodel_bisquare abline(mymodel_bisquare,col = "red")
#查看残差大的离群点权重是不是低
w_bisquare w_bisquare

以下给出一种循环保存多张图片的方法

#循环中保存图片
for (k in 1:100) {
  setwd("F:/picture") #规定R语言工作路径
  filename=paste("A",k,".jpeg") #利用循环使文件名各异
  jpeg(file = filename)
  plot(k,k+1)
  dev.off()
}

以下是最小二乘回归(绿直线)、Huber损失的M估计(蓝直线)、Bisquare损失的M估计(红直线)的对比图，黑线为真实直线。

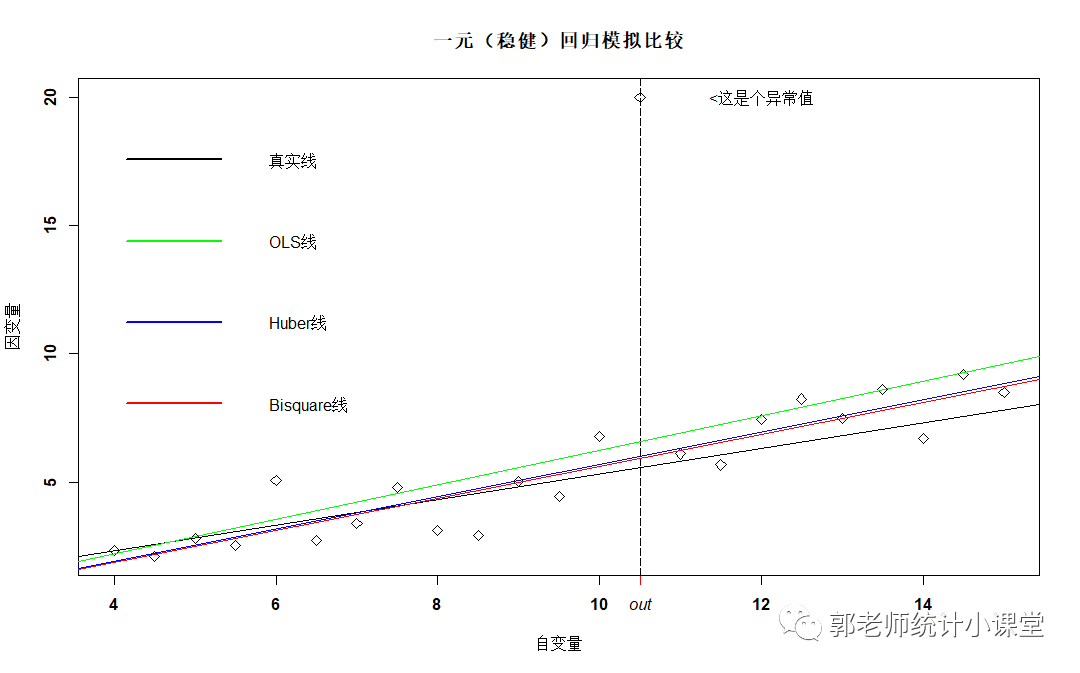
94a28bc8e55236dba15fa07facbd3239.png

可以看出稳健回归方法对离群值的干扰作用还是有很大的抵抗力的。

参考资料

  • 1.L1、L2损失函数、Huber损失函数，https://www.cnblogs.com/pacino12134/p/11104446.html
  • 2.R文档关于Bisquare，https://www.rdocumentation.org/packages/qrmix/versions/0.9.0/topics/Bisquare
如果觉得本文不错，请点赞关注！
8280f022beaeab62d91c639a12db96cd.png