Python求一组数字的最大公约数和最小公倍数

一、先来看求最大公约数

1）、利用gcd函数

math库里面有个gcd函数能直接求出两个数字的最大公约数，遇到求一组数字的最大公约数的时候，加一个循环就好，如下：

import math
def gcd_many(s):
    g = 0
    for i in range(len(s)):
        if i == 0:
            g = s[i]
        else:
            g=math.gcd(g,s[i])

    return g

s = list(map(int,input().split()))
print(gcd_many(s))

看输入输出：

输入：4 8 12 24 48
输出：4

2）、不使用库函数里面的gcd函数

不用gcd函数的话，我们就自己写一个求两个数最大公约数的函数，如下：

def gcd_2(a,b):		#求两个数的最大公约数
    a,b = max(a,b),min(a,b)
    if a%b == 0:
        return b
    else:
        return gcd_2(b,a%b)

def gcd_many(s):		#求全部的
    g = 0
    for i in range(len(s)):
        if i == 0:
            g = s[i]
        else:
            g=gcd_2(g,s[i])

    return g

s = list(map(int,input().split()))
print(gcd_many(s))

二、求一组数的最小公倍数

求最小公倍数没有捷径可走，我们知道小时候学的“短除法”求最小公倍数，就是将两个数所有的约数，乘到一起再乘以下面的两个数字，如图：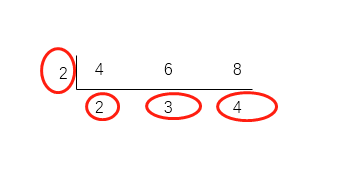

最小公倍数就是$2\ast 2\ast 3\ast 4$，所以只要求出最大公约数，在乘上每个数除以最大公约数的值即可。

不废话了，上代码：

import math
s = list(map(int,input().split()))
def gbs(s):
    a,b = s[0],s[1]
    a = a // math.gcd(a, b) * b // math.gcd(a, b) * math.gcd(a, b)
    if len(s)>2:
        for i in range(2,len(s)):
            b = s[i]
            a = a//math.gcd(a,b) * b//math.gcd(a,b) * math.gcd(a, b)
    return a

print(gbs(s))

看输入输出：

输入：10 16 4
输出：80

小白欢迎指点~