三种求平方根的算法——C/C++

1、二分法

这种是最简单的，就是定义一个最小值0和最大值number，把一个数取一个中间值（0+number）/2，然后平方，如果平方大于该数值，就把中间值赋给最大值，否者就把中间值赋给最小值，一直循环，直到取到想要的精度为止
代码如下：

//二分法 
double sqrt1(double x){
	double EPSINON = 0.00001;
	double low = 0.0;
	double high = x;
	double mid = (low + high) / 2;
	while ((high - low) > EPSINON){
		if (mid*mid > x){
			high = mid;
		}
		else{
			low = mid;
		}
		mid = (high + low) / 2;
	}
	return mid;
}

2、牛顿迭代法

这个也是有迹可循的，求平方根即x^2=n。
令f(x)=x^2-n
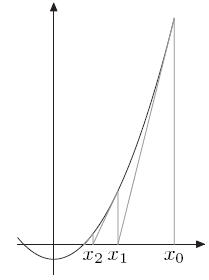
如图所示：
取x0，如果x0不是解，做一个经过(x0,f(x0))这个点的切线，与x轴的交点为x1。
同理，如果x1不是解，做一个经过(x1,f(x1))这个点的切线，与x轴的交点为x2。
以此类推。
以这样的方式得到的 xi 会无限趋近于 f(x)=0 的解。

判断xi是否是f(x)=0的解有两个步骤：

• 计算 f(xi) 的值，判断是否为 0
• 判断前后两个解 xi 和 xi-1 是否无限接近。

（1）先
(f(x)-f(xi))/(x-xi)=f’(x)，f’(x)是斜率也是f(x)的导函数，即f’(x)=2x。
化简得：f(xi)=f(x)-f’(x)(x-xi)，令f(xi)=0得：

(x^2-n)-2x(x-xi)=0

持续化简得：

x^2 - n - 2x^2 + 2xx_i=0
2xx_i=x^2 + n
2xi=x+n/x
xi=(x+n/x)/2

（2）再采用第二种方法判断
这样就得到了一元等式，就可以进行编程了。

//牛顿迭代法 
double sqrt2(double x) {
    if (x == 0) {
    	return 0;
    }
    double last = 0.0;
    double res = 1.0;
    while (res != last) {
        last = res;
        res = (res + x / res) / 2;
    }
    return res;
}

3、神秘代码

网上说出自Quake-III Arena (雷神之锤3)是90年代的经典游戏之一，作为游戏引擎算法。
直接上代码，我也不是很懂。

//神奇代码 
double sqrt3(double x) { 
	//float后加f转换成double类型
    if(x == 0) return 0; 
    float result = x; 
    float xhalf = 0.5f*result; 
    int i = *(int*)&result; 
    
    // what the fuck? 
    i = 0x5f3759df - (i>>1); 
    result = *(float*)&i; 
    result = result*(1.5f-xhalf*result*result);
    result = result*(1.5f-xhalf*result*result); 
    return 1.0f/result; 
}

中心思想是二分法，但是搞不懂为何求倒和0x5f3759df，为什么what the fuck? ，更加准确的是0x5f375a86。。。。

运行结果，多方面比较，采用C/C++的#include<math.h>库，引用sqrt对比

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

double sqrt1(double x);
double sqrt2(double x);
double sqrt3(double x);

int main() {
	const int count = 1000;		//测试次数 
	double test = 0.0;
	printf("sqrt\t\tsqrt1\t\tsqrt2\t\tsqrt3\n");
	for (int i = 0; i < count; i++) {
		test = rand() % 10000;
		double s = sqrt(test);
		double s1 = sqrt1(test);
		double s2 = sqrt2(test);
		double s3 = sqrt3(test);
		printf("%lf\t%lf\t%lf\t%lf\n", s, s1, s2, s3);
	}
	return 0;
}

总结

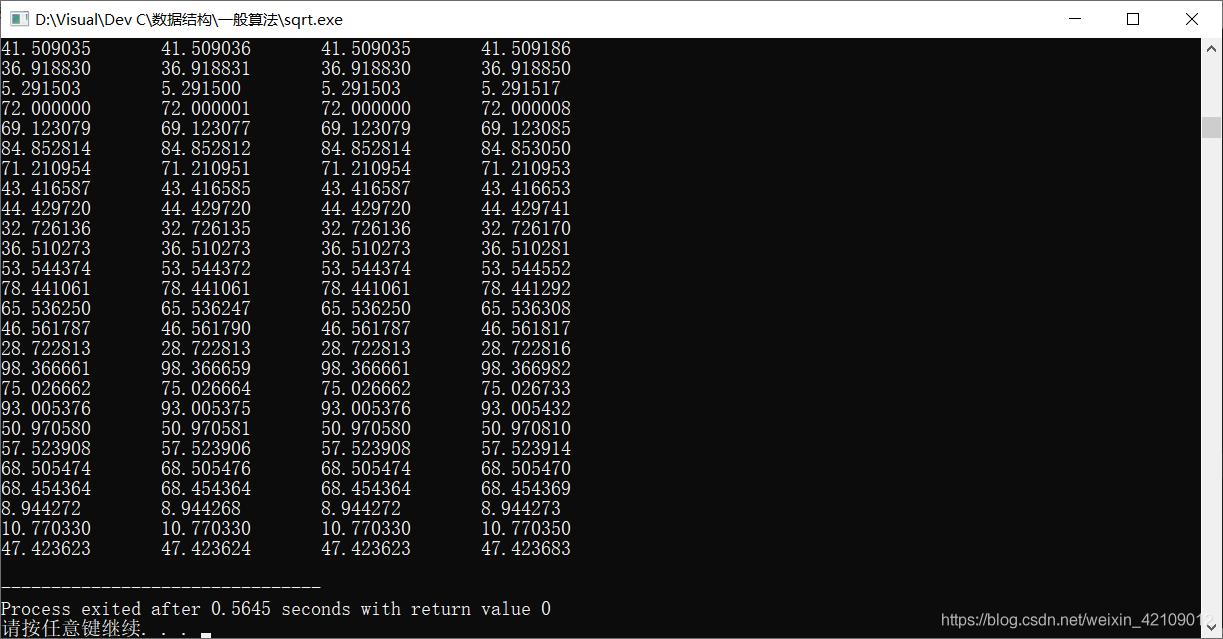
1、准确性
<math.h>的求平方根和牛顿迭代法一样

2、耗时
<math.h>的求平方根最短，可能直接底层运算吧。