通俗易懂理解卷积神经网络CNN

https://www.zhihu.com/question/22298352

1. 卷积

从数学上讲，卷积就是一种运算，就是一个函数在另一个函数上的加权叠加。

2. 卷积的定义

我们称$(f\ast g)(n)$为$f,g$的卷积

其连续的定义为：

$(f\ast g)n={\int }_{-\infty }^{\infty }f(\tau )g(n-\tau )d\tau$

其离散的定义为：

$(f\ast g)(n)={\sum }_{\tau =-\infty }^{\infty }f(\tau )g(n-\tau )$

这两个式子有一个共同的特征：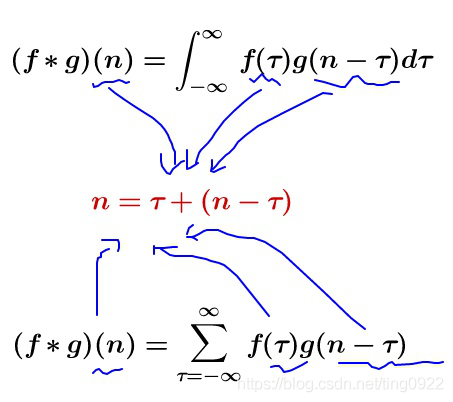

这个特征有什么意义？
我们令$x=\tau ,y=n-\tau$，那么$x+y=n$就是下面的这些直线：

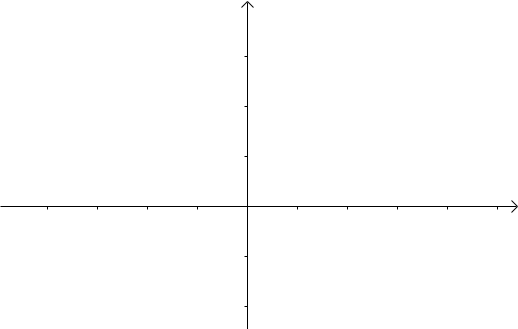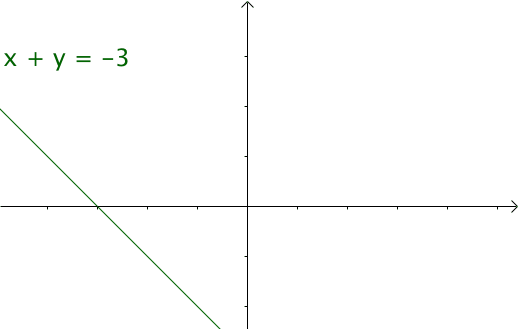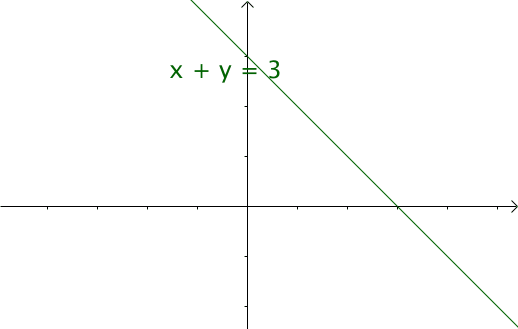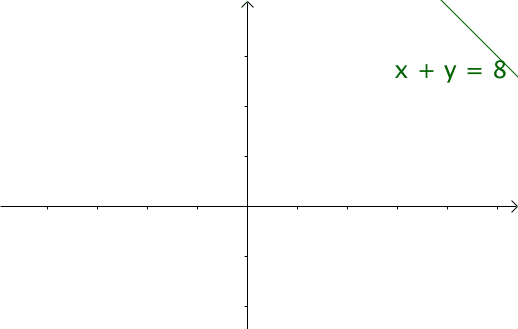
如果遍历这些直线，就好比，把毛巾沿着角卷起来：

只看数学符号，卷积是抽象的，但是，我们可以通过现实中的意义，来习惯卷积这种运算。

3.离散卷积的例子：求骰子

我有两枚骰子

把这两枚骰子都抛出去，求：两枚骰子点数加起来为4的概率是多少？
这个问题的关键是，两枚骰子加起来要等于4， 这正是卷积的应用场景。
我们把骰子各个点数出现的概率表示出来：

那么这两枚骰子点数加起来为4的情况有：

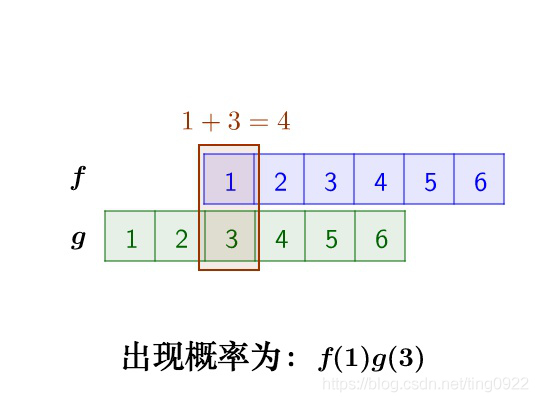
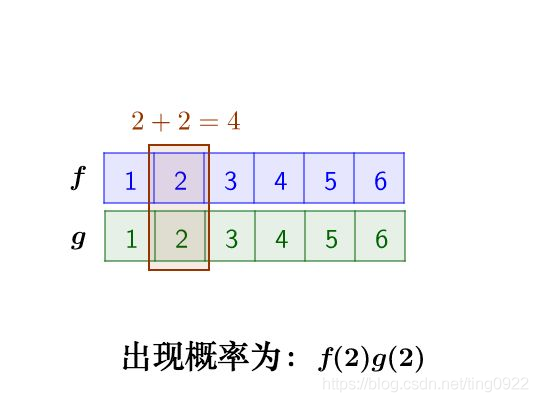
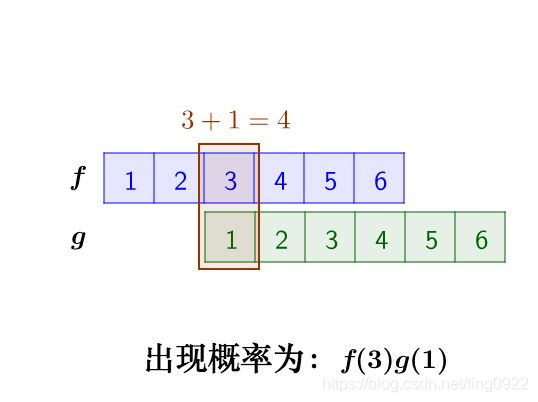
因此，两枚骰子点数加起来为4的概率为：

$f(1)g(3)+f(2)g(2)+f(3)g(1)$

符合卷积的定义，把它写成标准的形式就是：

$(f\ast g)(4)={\sum }_{m=1}^{3}f(4-m)g(m)$

4.连续卷积的例子：做馒头

楼下早点铺子生意太好了，供不应求，就买了一台机器，不断的生产馒头。

假设馒头的生产速度是$f(t)$，那么一天后生产出来的馒头总量为：

${\int }_0^{24}f(t)dt$

馒头生产出来之后，就会慢慢坏掉，这个坏掉的函数为$g(t)$。第一个小时做出来的馒头，一天后经历24小时的坏掉的过程，第二个小时生产出来的馒头，一天后经历23小时的坏掉的过程。
如此，我们可以知道，一天后，馒头总共坏掉了：

${\int }_0^{24}f(t)g(24-t)dt$

这就是连续的卷积。

5.图像处理

5.1 原理

有这么一副图像，可以看到，图像上有很多噪点：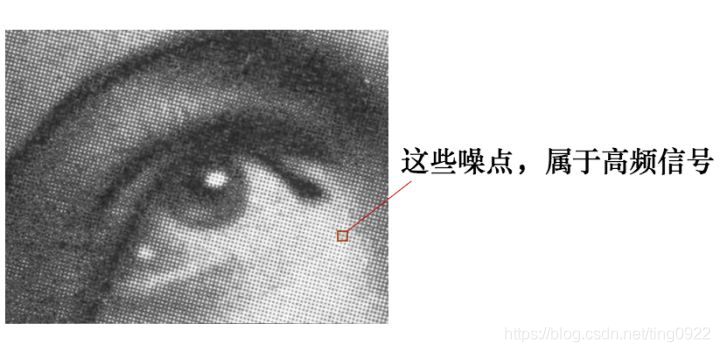

高频信号，就好像平地耸立的山峰：

看起来很显眼，平滑这座山峰的方法之一就是把山峰刨掉一些土，填到山峰周围去。用数学的话来说，就是把山峰周围的高度平均一下。

平滑后得到：

5.2 计算

卷积可以帮助实现这个平滑算法。
有噪点的原图，可以把它转为一个矩阵：

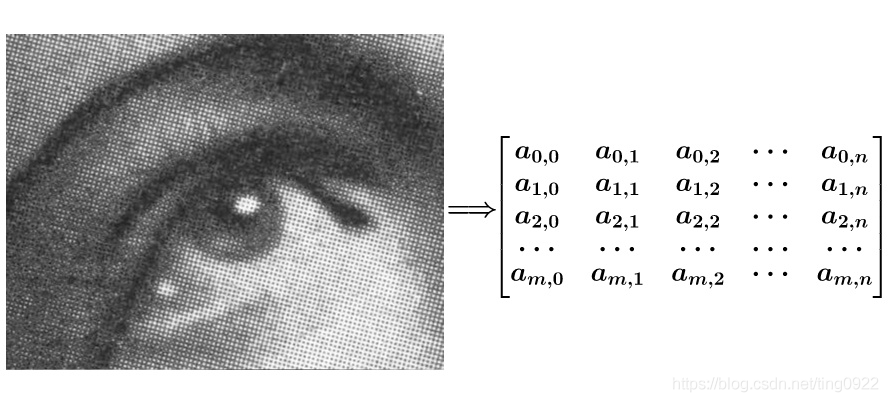
然后用下面这个平均矩阵（说明下，原图的处理实际上用的是正态分布矩阵，这里为了简单，就用了算术平均矩阵）来平滑图像：

$g=\left[\begin{array}{ccc}1/9& 1/9& 1/9\\ 1/9& 1/9& 1/9\\ 1/9& 1/9& 1/9\end{array}\right]$

把高频信号与周围的数值平均一下就可以平滑山峰。
比如我要平滑$a_{1,1}$点，就在矩阵中，取出$a_{1,1}$点附近的点组成矩阵$f$，和$g$进行卷积计算后，再填回去：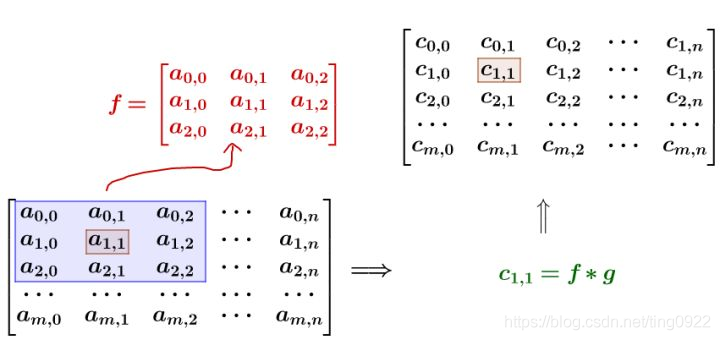

要注意一点，为了运行卷积，$g$虽然和$f$同维度，但是下标却不一样：
用一个动图来说明计算过程：

写成卷积公式就是：

$(f\ast g)(1,1)={\sum }_{k=0}^2{\sum }_{h=0}^{2}f(h,k)g(1-h,1-k)$

这样就相当于实现了$g$这个矩阵在原来图像上的滑动（准确来说，下面这幅图把$g$矩阵旋转了180度）：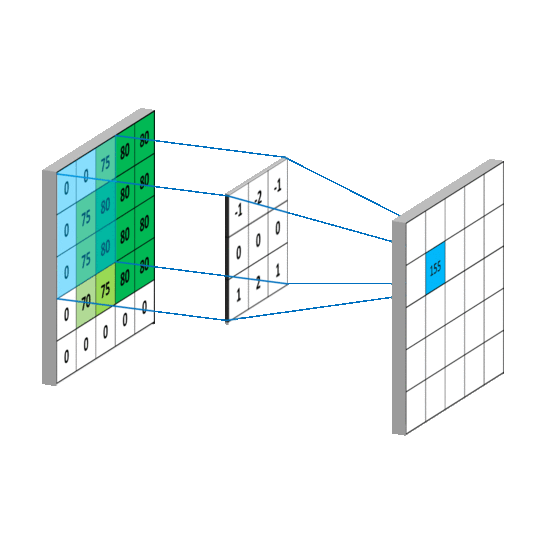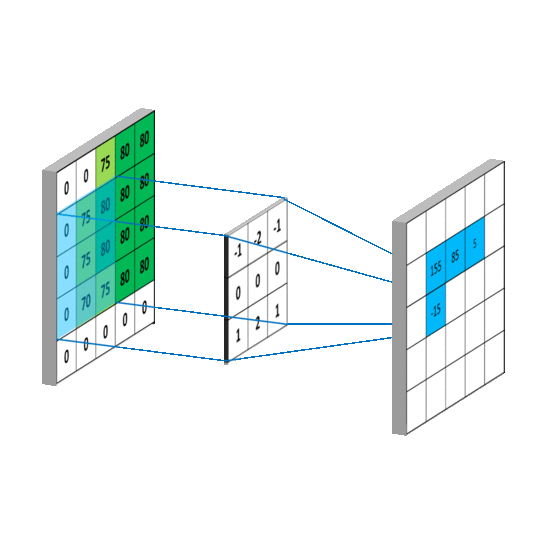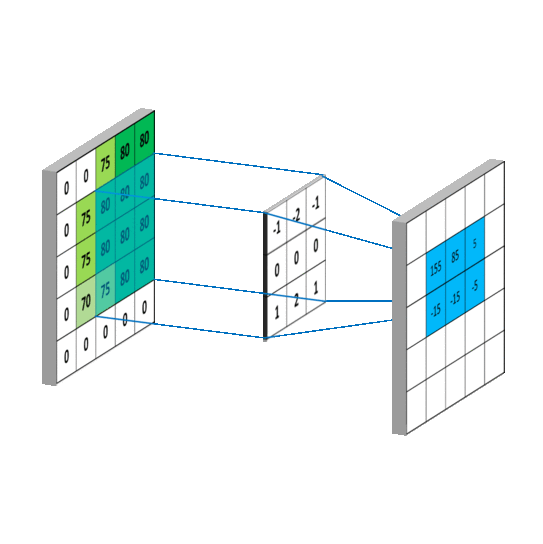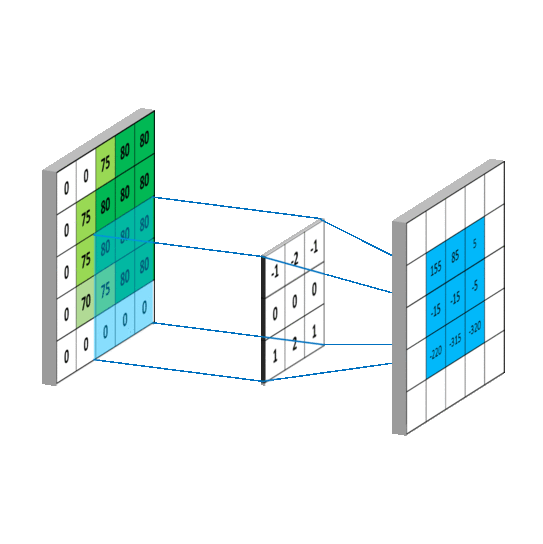

这个图展示的其实就是卷积神经网络中的卷积层做的事情。