线性代数小结02伴随矩阵的十二个性质

性质一

$A^{*}A=E$

性质二

$(\lambda A)^{*}=\lambda ^{n-1}A^{*}$

性质三

$A^{*}$ 可逆的充要条件是 $A$ 可逆

证明

充分性

显然的

必要性

证明伴随矩阵可逆，原矩阵必然可逆

假设A不可逆，那么A的行列式为0，有

$AA^{*}=\left | A \right |E=O$

$AA^{*}(A^{*})^{-1}=0$

$A=E$

$A^{*}=O$

零矩阵不可逆，得出矛盾

性质四

矩阵的伴随矩阵的转置矩阵等于矩阵的转置矩阵的伴随矩阵

$(A^{*})^{T}=(A^{T})^{^{*}}$

暴力求证

得证

性质五

对称矩阵的伴随矩阵也是对称矩阵

$(A^{*})^{T}=(A^{T})^{*}=A^{*}$

性质六

<1>正交矩阵的伴随矩阵是正交矩阵

$\because A.is-orthogonal \therefore AA^{T}=A^{T}A=E;\left | A \right |^{2}=1 \because AA^{*}=\left | A \right |E$

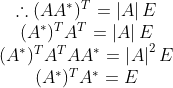
$\begin{matrix} \therefore (AA^{*})^{T}=\left | A \right |E\ (A^{*})^{T}A^{T}=\left | A \right |E\ (A^{*})^{T}A^{T}AA^{*}=\left | A \right |^{2}E\ (A^{*})^{T}A^{*}=E\ \end{matrix}$

<2>矩阵的伴随矩阵为正交矩阵,那么矩阵数乘其行列式的倒数也是正交矩阵

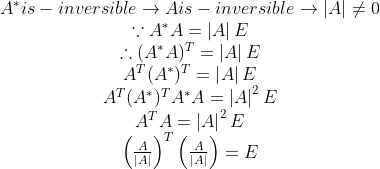
$\begin{matrix} A^{*} is-inversible\rightarrow Ais-inversible\rightarrow \left | A \right |\neq 0\ \because A^{*}A=\left | A \right |E\ \therefore (A^{*}A)^{T}=\left | A \right |E\ A^{T}(A^{*})^{T}=\left | A \right |E\ A^{T}(A^{*})^{T}A^{*}A=\left | A \right |^{2}E\ A^{T}A=\left | A \right |^{2}E\ \left ( \frac{A}{\left | A \right |} \right )^{T}\left ( \frac{A}{\left | A \right |} \right )=E \end{matrix}$

性质七

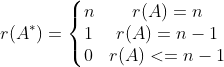
$r(A^{*})=\left\{\begin{matrix} n & r(A)=n\ 1 & r(A)=n-1\ 0 & r(A)<=n-1 \end{matrix}\right.$

见小结01

性质八

<1>一个二阶以上可逆矩阵的m重伴随矩阵

$A^{*^{m}}=\left | A \right |^{\frac{(n-1)^{m}+(-1)^{m-1}}{n}}A^{(-1)^{m}}$

<2>一个三阶以上的不可逆矩阵的重伴宿矩阵为零矩阵

<3>一个二阶的不可逆矩阵的m重伴随矩阵

$A^{*^{m}}=\left\{\begin{matrix} A & m=2k\ A^{*}& m=2k-1 \end{matrix}\right.$

待证明

性质九

若两矩阵相似,那么他们与自己的伴随矩阵的乘积相等

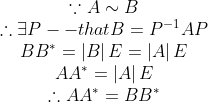
$\begin{matrix} \because A\sim B\ \therefore \exists P-- that B=P^{-1}AP\ BB^{*}=\left | B \right |E=\left | A \right |E\ AA^{*}=\left | A \right |E\ \therefore AA^{*}=BB^{*} \end{matrix}$

性质十

<1>若 $\lambda$ 为可逆矩阵 $A$ 的一个特征值, $\xi$ 是 $A$ 的属于特征值为 $\lambda$ 的特征向量,则 $\frac{\left | A \right |}{\lambda }$ 是 $A^{*}$ 的特征值, $\xi$ 是 $A^{*}$ 的属于特征值为 $\frac{\left | A \right |}{\lambda }$ 的特征向量

$A\xi =\lambda \xi$

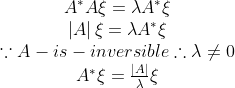
$\begin{matrix} A^{*}A\xi =\lambda A^{*}\xi \ \left | A \right |\xi =\lambda A^{*}\xi \ \because A-is-inversible\therefore \lambda \neq 0\ A^{*}\xi =\frac{\left | A \right |}{\lambda }\xi \ \end{matrix}$ $\begin{matrix} \\ \\ \\ \\ \end{matrix}$

<2>若可逆矩阵与对角矩阵相似,那么他的伴随矩阵也与对角矩阵相似

由<1>易得

性质十一

非可逆矩阵的一个非零特征值对应的一个特征向量是原矩阵的伴随矩阵属于特征值为零的特征向量

$A\xi =\lambda \xi$

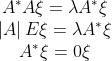
$\begin{matrix} A^{*}A\xi =\lambda A^{*}\xi \ \left | A \right |E\xi =\lambda A^{*}\xi \ A^{*}\xi =0\xi \ \ \end{bmatrix}$

性质十二

一个秩比阶数小一的矩阵与对角阵相似的充要条件是他的伴随矩阵的迹不等于0

复杂，待证明

原文链接：https://blog.csdn.net/Chandler_river/article/details/124453955