摘要

1. 提出了两种新颖的模型结构用来计算词向量
2. 采用一种词相似度的任务来评估对比词向量质量
3. 大量降低模型计算量可以提升词向量质量
4. 进一步，在我们的语义和句法任务上，我们的词向量是当前最好的效果

介绍

1. 传统NLP把词当成最小单元处理．并且能够在大语料上得到很好的结果，其中一个例子是N-grams模型
2. 然而很多自然语言处理任务只能提供很小的语料，如语音识别、机器翻译，所以简单地扩大数据规模来提升简单模型的表现在这些任务不再适用，所以我们必须寻找更加先进的模型
3. 分布式表示可以在大语料上训练得到很好的语言模型，并且能过超过N-grams模型，这是一个很好的可以作为改进的技术

NNLM

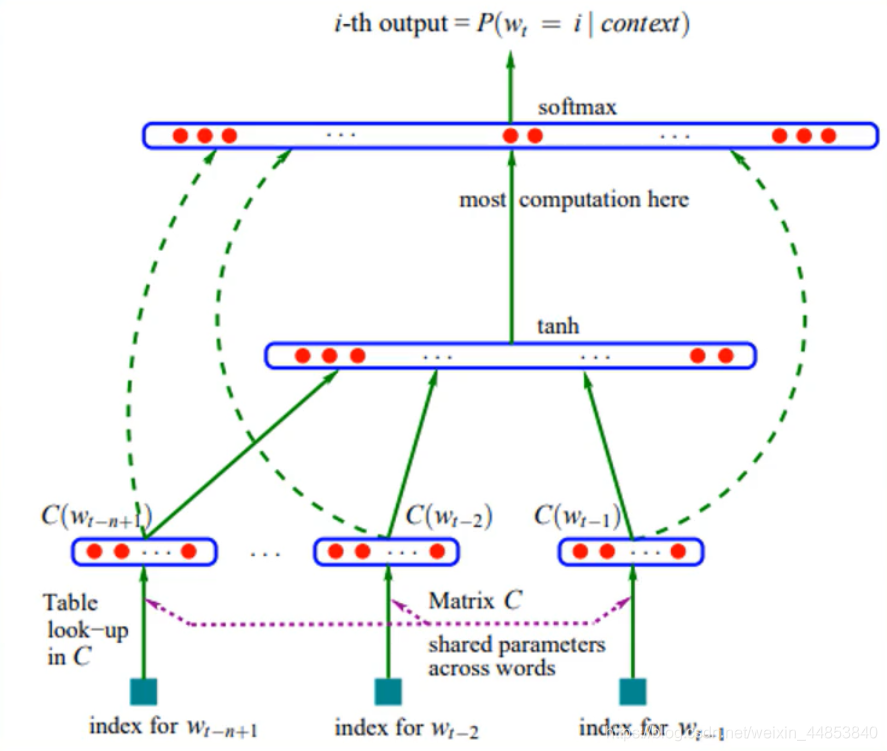
1. 根据前n -1个单词，预测第n个位置单词的概率
2. 优化模型，使得输出的正确的单词概率最大化

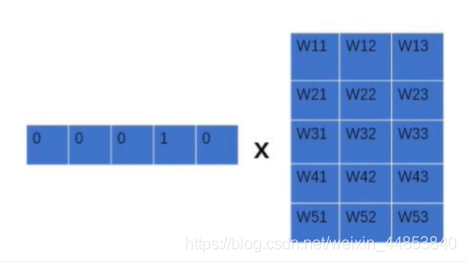
输入层：将词映射成向量,相当于一个1×V的one-hot向量乘以一个V xD的向量得到一个1×D的向量
隐藏层∶一个以tanh为激活函数的全连接层：a=tanh(d+ Ux)
输出层∶一个全连接层，后面接—个softmax函数来生成概率分布，y =b +Wa（其中y是一个1×V的向量）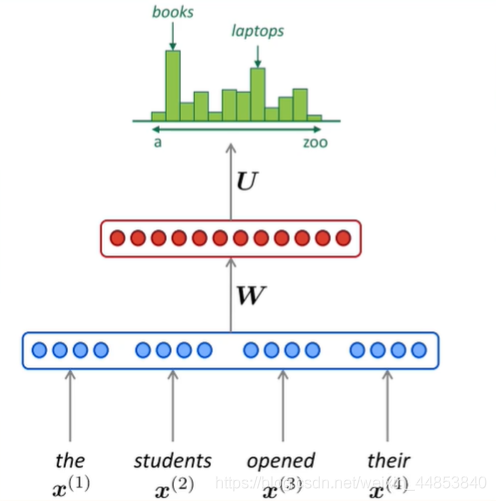

1. 仅对一部分输出进行梯度传播。
2. 引入先验知识，如词性等。
3. 解决一词多义问题。
4. 加速softmax层。

RNNLM

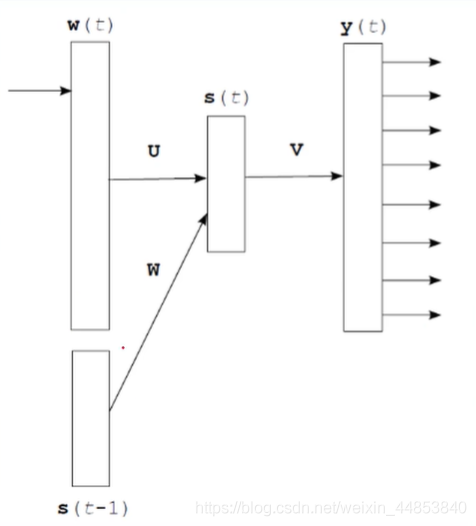
输入层：和NNLM一样，需要将当前时间步的转化为词向量
隐藏层：对输入和上一个时间步的隐藏输出进行全连接层操作:s(t)= Uw(t)+Ws(t -1)+d
输出层：一个全连接层，后面接一个softmax函数来生成概率分布：y(t)= b +Vs(t)，其中y是一个1×V的向量

每个时间步预测一个词,在预测第n个词时使用了前n- 1个词的信息。

Word2vec

Log-linear model

定义(Log Linear Models):将语言模型的建立看成一个多分类问题，相当于线性分类器加上softmax，Y = softmax(wx＋b)

原理

• 语言模型基本思想:句子中下一个词的出现和前面的词是有关系的,所以可以使用前面的词预测下一个词。
• Word2vec基本思想:句子中相近的词之间是有联系的，比如今天后面经常出现上午，下午和晚上。所以Word2vec的基本思想就是用词来预测词，skip-gram使用中心词预测周围词，cbow使用周围词预测中心词。

Skip-gram

Skip-gram 是使用中间词作为输入，期待模型输出为周围的词。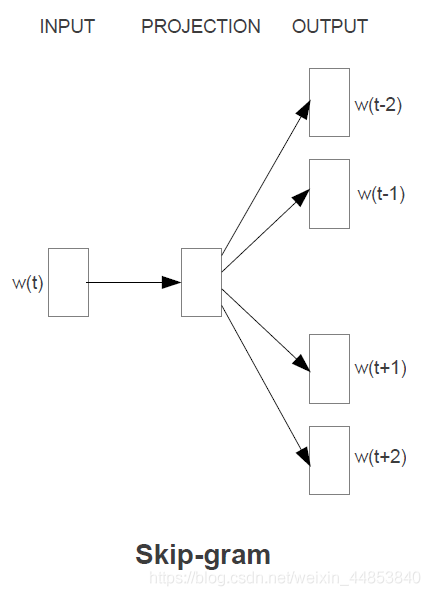


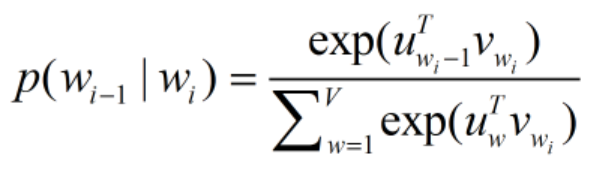
用中心词向量和周围词向量做累计：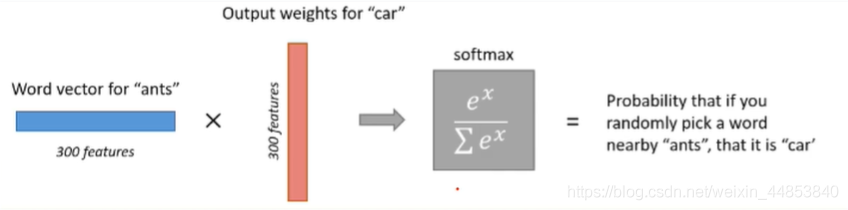
给定词序列 w1,w2,w3,…,wT，Skip-gram model 的目标函数是最大化下式：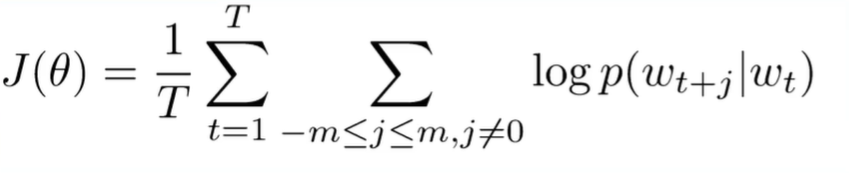

其中 c 是窗口大小，T 是词序列的长度。logp(wt+j|wt) 是以中间词为输入，输出周围词的概率。这个模型的目标就是最大化周围词的概率。

其中 p(wt+j|wt) 该如何计算呢？

从前面模型的结构图可以知道，一个词对应两个向量，设：

• vwI 表示词 w 在第一个矩阵中的向量
• uwO 表示词 w 在第二个矩阵中的向量

如此以来，以词 wI 作为输入，词 wo 对应的概率为：

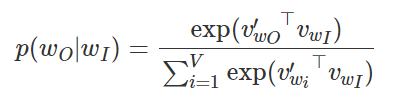
CBOW

CBOW 是利用周围的词作为模型输入，预测中间的词。即以周围的词作为输入，采用一个分类模型，期待的输入是中间的词。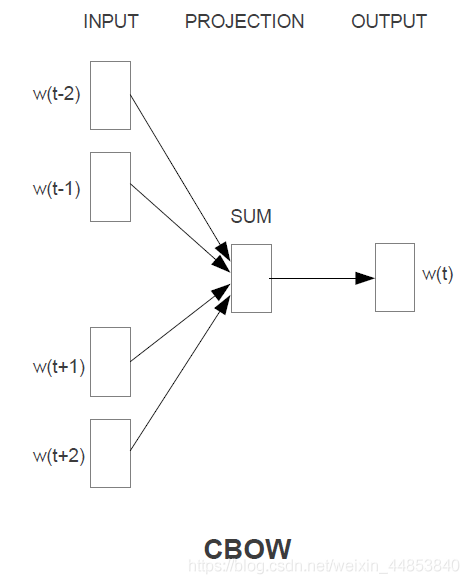


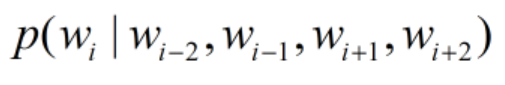
e1,e2,e3,e4上下文词

$$u_o=sum(e_1,e_2,e_3,e_4)$$

损失函数：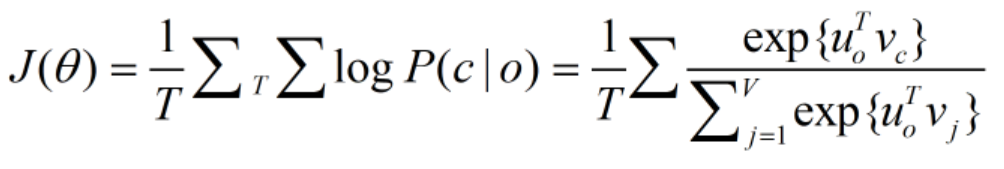

复杂度

层次softmax：把softmax的计算转化成求sigmoid计算，利用二叉树进行二分法，总共需要计算log2V个sigmoid。
当然还有更快的方法——构建Huffman树，带权重路径最短二叉树。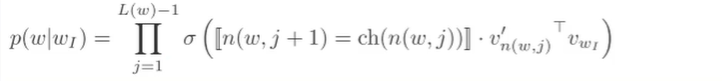

• L(w)树高度O(log2V)
• n(w,j)词w在树上的第j个节点
• n(w,1) root
• n(w,L(w)) =w叶子
• ch(n(w, j))=n(w,j ＋1)= ch(n(w,j))
• VwI中心词的词向量
• Vn(w,j)词w在树上的第j个节点的分数

负采样：舍弃多分类，提升速度，将多分类问题转化成二分类问题。
增大正样本概率，减小负样本概率对于每个词，一次要输出1个概率,总共K+1个，K<<V，并且效果比多分类要好，这里还是需要每个词的上下文词向量,总的参数比HS多(每次计算量不多)。

重采样：想更多地训练重要的词对，比如训练“France"和"Paris"之间的关系比训练“France”和“the"之间的关系要有用；高频词很快就训练好了，而低频次需要更多的轮次。重采样方法:
$$P(w_i)=1-\sqrt{\frac{t}{f(w_i)}}$$
其中f(wi)为词wi在数据集中出现的频率。文中t选取为10^-5，训练集中的词wi会以P(wi)的概率被删除。
词频越大，f(wi)越大,P(wi)越大，那么词wi就有更大的概率被删除，反之亦然。如果词wi的词频小于等于t,那么wi则不会被剔除。
优点:加速训练，能够得到更好的词向量。

模型复杂度

• O=E×T×Q
• O是训练复杂度training complexity
• E是训练迭代次数number of the training epochs
• T是数据集大小number of the words in the training set
• Q是模型计算复杂度model computational complexity

$$Q=V\ast H+N\ast D\ast H+N\ast D$$

• x维度N*D
• U维度V*H
• W维度ND H
• N个上文词
• D词向量维度
• V词表的大小
• H隐藏层大小

模型复杂度对比：

• 前馈神经网络：Q=N* D＋N*D *H＋H * log2V
• 循环神经网络：Q=H*H＋H * log2v
• CBOW+HS：Q =N*D＋D * log2V
• Skip-Gram+HS: Q =C(D+D * log2V)
• CBOW+NEG: Q=N*D＋D *(K＋1))
• Skip-Gram+NEG: Q =C(D+D *(K+1))

实验结果

最大化正确率（优化参数）：

• 用小数据集调参，选择最好的参数
• 维度，以及训练数据量，是2个需要寻找的参数

模型比较：

• RNNLM单机用了8周NNLM计算量更大
• RNN相对在语法问题上更好
• NNLM效果更好
• CBOW更好
• Skip-gram更平衡,在语义问题上效果好
• 3 epoch>1 epoch；3 epoch 300dim<1 epoch 600dim

研究意义

1. 衡量词向量之间的相似度
2. 作为预训练模型提升nlp任务

总结

关键点

• 更简单的预测模型——Word2vec
• 更快的分类方案——HS和NEG

创新点

1. 提出一种新的结构：简化了结构，大大减小了计算量从而可以使用更高的维度，更大的数据量
2. 利用分布式训练框架：在大数据上训练，从而达到更好的效果
3. 提出了新的词相似度任务：Analogy词类别

使用词对的预测来替代语言模型的预测；使用HS和NEG降低分类复杂度；使用subsampling加快训练；新的词对推理数据集来评估词向量的质量。

启发点

• 大数据集上的简单模型往往强于小数据集上的复杂模型：simple models trained on huge amounts of data outperform complex systems trained on lessdata.
• King的词向量减去Man的词向量加上Woman的词向量和Queen的词向量最接近：vector(“King”) - vector(“Man”)+ vector(“Woman”) results in a vector that is closest to the vectorrepresentation of the word Queen.
• 我们决定设计简单的模型来训练词向量，虽然简单的模型无法像神经网络那么准确地表示数据，但是可以在更多地数据上更快地训练：we decided to explore simpler models that might not be able to represent the data as precisely asneural networks, but can possibly be trained on much more data efficiently.
• 我们相信在更大的数据集上使用更大的词向量维度能够训练得到更好的词向量：We believe that word vectors trained on even larger data sets with larger dimensionality willperform significantly better.