目录
1. 向量是什么
有数值大小, 有方向的矢量
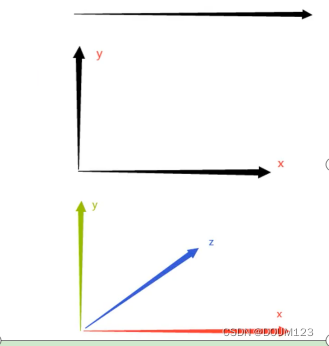
在Unity里一个Vector3类型的数值例如(1,2,1), 既可以表示一个点, 也可以表示一个由原点指向这个点的向量
位置—— 代表一个点
this.transform.position
方向—— 代表一个方向
this.transform.forward
可以理解为以世界坐标系为基准的偏移值
2. 向量的计算
两个点就能决定一个向量
要计算一个由A点指向B点的向量的话, 只需用B点坐标减去A点坐标即可
即终点减起点
Vector3AB = B - A;
Vector3BA = A - B;
3. 向量的模长
向量的模长就是向量的长度
也就是两个点之间的距离
AB.magnitude
4. 单位向量
模长为1的向量, 任意向量经过归一化就是单位向量
一般用于表示方向, 忽略大小
AB.normalized
或者
AB / AB.magnitude(向量除以向量的模长)
5. 向量的加减乘除
1) 向量的加法
向量A(Xa, Ya, Za)
向量B(Xb, Yb, Zb)
A + B = (Xa + Xb, Ya + Yb, Za + Zb)
位置 + 向量
位置+向量 = 新位置
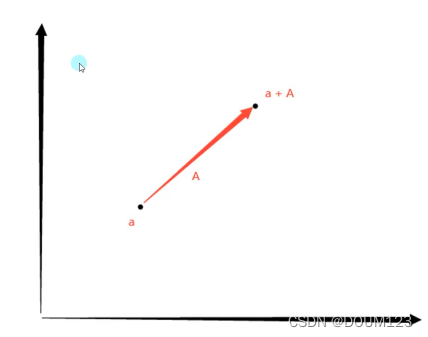
向量 + 向量
向量 + 向量 = 新向量
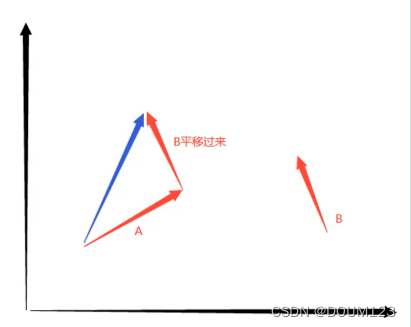
2) 向量减法
向量A(Xa, Ya, Za)
向量B(Xb, Yb, Zb)
A - B = (Xa - Xb, Ya - Yb, Za - Zb)
位置 - 位置
位置 - 位置=向量
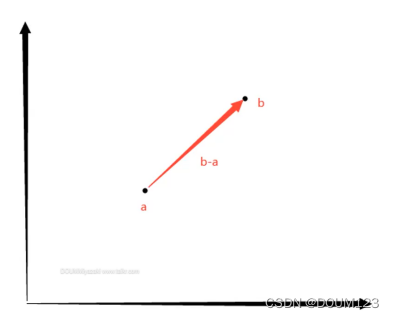
向量 - 向量
向量 - 向量= 新向量
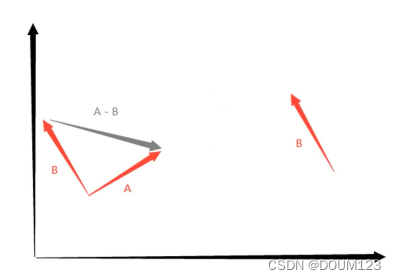
位置 - 向量
位置 - 向量 = 新位置
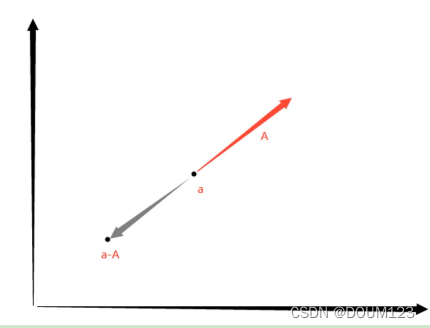
3) 向量乘除
向量只能和标量进行乘除法运算
向量A(x, y, z)
标量a
A * a = (x*a, y*a, z*a)
A / a = (x/a, y/a, z/a)
向量乘除标量为新向量
向量乘除正数, 方向不变, 放大缩小模长
向量乘除负数, 方向相反, 放大缩小模长
向量乘除零, 得到零向量
4) 向量加减乘除总结
向量加法--位置平移或向量计算
向量减法--位置平移或向量计算
向量乘除--模长放大缩小
6. 向量的点乘
1) 计算公式
向量A(Xa, Ya, Za)
向量B(Xb, Yb, Zb)
A ・ B = Xa * Xb + Ya * Yb + Za * Zb
向量 * 向量 = 标量
2) 几何意义
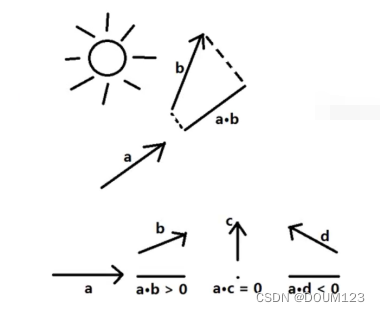
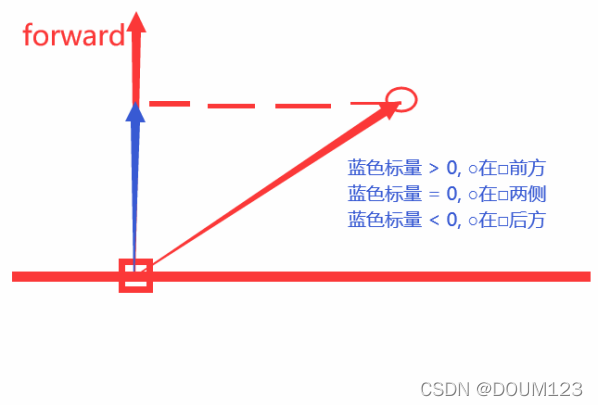
点乘可以得到一个向量在自己向量上投影的长度
3) 通过点乘算大致方位
点乘结果 > 0, 两向量夹角为锐角
点乘结果= 0, 两向量夹角为直角
掉秤结果 < 0, 两向量夹角为钝角
float dotResult = Vector3.Dot(this.transform.forward, target.position -
this.transform.position);
if( dotResult >= 0 )
{
print("它在我前方");
}
else
{
print("它在我后方");
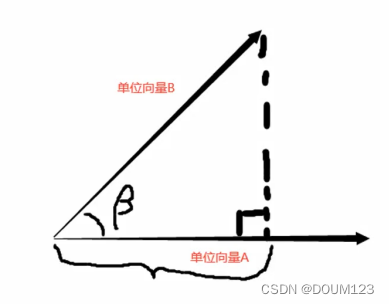
}4) 通过点乘算两向量夹角
两向量夹角 = 两向量的点乘的反余弦
//1.用单位向量算出点乘结果
float dotResult = Vector3.Dot(this.transform.forward, (target.position - this.transform.position).normalized);
//2.用反三角函数得出角度
print("角度-" + Mathf.Acos(dotResult) * Mathf.Rad2Deg);5) 点乘总结
可以判断对象的方位
可以计算两个向量之间的夹角
7. 向量的叉乘
1) 计算公式
向量A(Xa, Ya, Za)
向量B(Xb, Yb, Zb)
A * B = (YaXb - XaYb, ZaXb - XaZb, XaYb - YaXb)
2) 几何意义
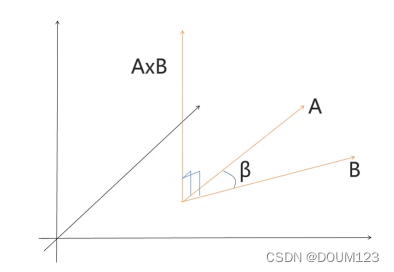
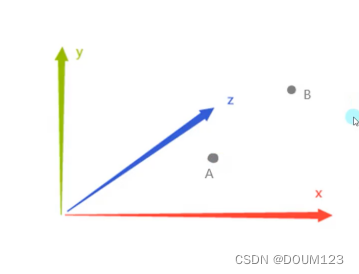
1. 叉乘得到的向量同时垂直于两个向量
2. 叉乘得到的向量 y 如果大于0, 则证明 B 在 A 右侧, 如果 y 小于0, 则证明 B 在 A 左侧
public Transform A;
public Transform B;
void Start()
{
Vector3.Cross(A.position, B.position)
}
void Update()
{
Vector3 C = Vector3.Cross(A.position, B.position);
if (C.y > 0)
{
print("B在A的右侧");
}
else
{
print("B在A的左侧");
}
}