 解题思路:
解题思路:
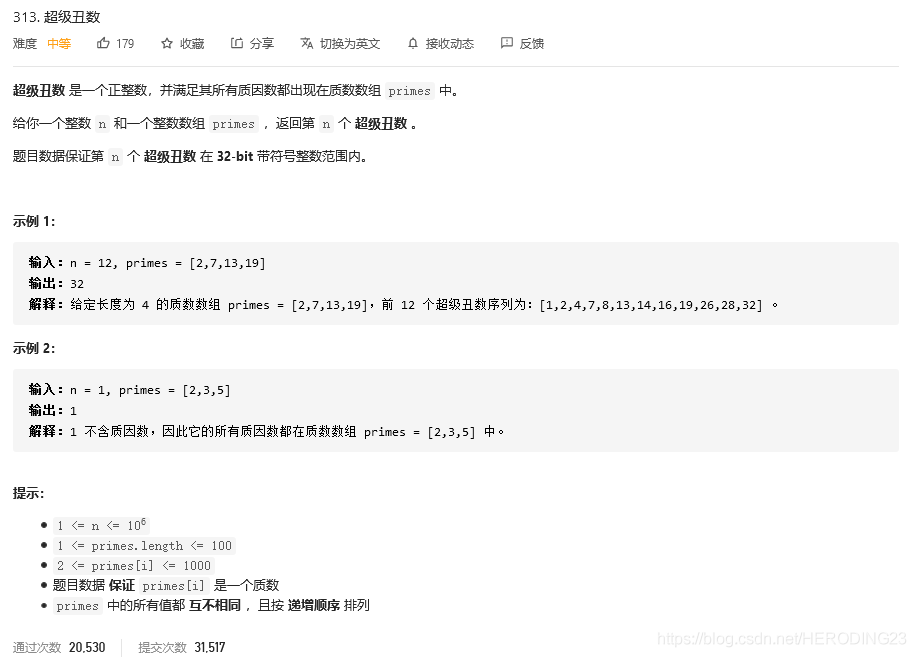
作为丑数II的变形,这里只是将2,3,5替换成了数组的形式,其他都没有变化,可以参考丑数II进一步理解,这里我简单解释一下,首先1是所有数的因数,所以一定放在第一个,那么从1开始,所有的丑数都是由数组中的元素组成,也就是说,都是数组中元素的倍数,所以另建一个倍数系数数组,每当找到最小的倍数与对应的元素相乘是当前找到的最小的,就作为dp[i],并更新倍数(倍数++),如果检查有无遇到最小值相同,因为dp数组是无重复的,找到直接相应倍数++,代码如下:
class Solution {
public:
int nthSuperUglyNumber(int n, vector<int>& primes) {
int len = primes.size();
vector<int> count(len, 1);
// 初始化丑数数组
vector<int> dp(n + 1);
dp[1] = 1;
// 从第二个丑数开始
for(int i = 2; i <= n; i ++) {
int index = 0, num = INT_MAX;
for(int j = 0; j < len; j ++) {
if(dp[count[j]] * primes[j] < num) {
index = j;
num = dp[count[j]] * primes[j];
}
}
count[index] ++;
dp[i] = num;
// 更新重复项
for(int j = 0; j < len; j ++) {
if(dp[count[j]] * primes[j] == num) {
count[j] ++;
}
}
}
return dp[n];
}
};
还有最小堆的方法,步骤更加简略,但是最小堆的实现还是很消耗时间和空间的,代码如下:
class Solution {
public:
int nthSuperUglyNumber(int n, vector<int>& primes) {
unordered_set<long> seen;
priority_queue<long, vector<long>, greater<long>> heap;
seen.insert(1);
heap.push(1);
int ugly = 0;
for (int i = 0; i < n; i++) {
long curr = heap.top();
heap.pop();
ugly = (int)curr;
for (int prime : primes) {
long next = curr * prime;
if (seen.insert(next).second) {
heap.push(next);
}
}
}
return ugly;
}
};
版权声明:本文为HERODING23原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。