定义:
【1】独立事件在给定区间内随机发生,给定区间为时间或空间
【2】已知该区间内的事件平均发生次数(发生率),用希腊字母 λ(lambda)表示。
举例:
某电影院的爆米花机总是坏,顾客们很不高兴。下星期电影院有一个大型促销活动,经理希望爆米花机不要出状况,已知爆米花机每一周的平均故障次数为3.4,或者说爆米花机的故障率为3.4。那么爆米花机下一周不发生故障的概率有多大?泊松分布就是用来解决这类问题的。

用X表示给定区间内的事件发生次数,如果X符合泊松分布,且每个区间内平均发生λ次,或者说发生率为λ,则写作:
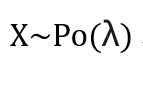
省去推导过程,直接给出概率公式:
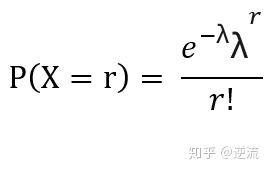
泊松分布的期望和方差
如果X~Po(λ) ,则E(X)为给定区间内能够期望的事件发生次数,对于爆米花机来说,为在一周内能够期望的机器损坏次数,也就是说,E(X)是给定区间内的事件平均发生次数。
因此泊松分布的期望和方差非常的简洁,因为它的期望和方差都等于λ。
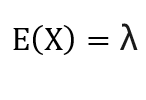
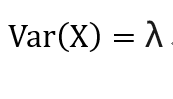
泊松分布的形状
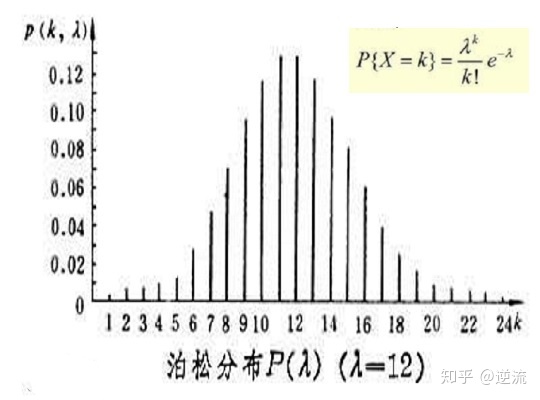
泊松分布的形状随着λ的数值发生变化。λ小,则分布向右偏斜,随着λ变大,分布逐渐变的对称。如果λ是一个整数,则有2个众数,λ和λ-1,如果λ不是整数,则众数为λ。
例题:
某电影院的爆米花机总是坏,顾客们很不高兴。下星期电影院有一个大型促销活动,经理希望爆米花机不要出状况,已知爆米花机每一周的平均故障次数为3.4,或者说爆米花机的故障率为3.4。
(1)下一周爆米花机不发生故障的概率是多少?
P(X=0) = e^-λ / r!
= e^-3.4 x 3.4^0
=e^-3.4 = 0.033
(2)下一周爆米花机发生3次故障的概率是多少
P(X = 3) =e^-3.4 x 3.4^3 / 3!
=e^-3.4 x 39.304 / 6
=0.033 x 6.55 = 0.216
(3)爆米花机发生故障的期望和方差是多少?
E(X) = λ =3.4
Var(X) = λ =3.4
组合泊松变量
假如我们不止有爆米花机,还有饮料机,饮料机每周发生故障的平均次数2.3,求下个星期两个机器总故障次数为0的概率。
我们把爆米花机故障事件设为X,饮料机故障事件设为Y,即求P(X+Y=0)
因为X和Y是独立变量,因此:
P(X+Y) =P(X)+P(Y)
E(X+Y) =E(X)+E(Y)
所以总故障事件可以写作:X+Y~Po(λx+λy),此事件的λ=3.4+2.3=5.7
P(X+Y=0) = e^-5.7 x5.7^0 / 0!
=e^-5.7 x 1/1 =0.003
泊松分布与二项式分布的关系
举例:小红在曲奇饼厂工作,她的工作是确保每一盒饼干都符合工厂严格的质量要求,她知道每块饼干发生破碎的概率为0.1,她的老板要求她求出一盒容量为100块的饼干的盒子里出现15块碎饼干的概率,她认为很简单,说用二项式分布公式计算就好了,X~B(n=100,p=0.1)。可是她拿出计算器计算100!时,计算器显示出错,因为数字太大!

要解决上面提到的问题,就会用到泊松分布,因为有时候,使用泊松分布比使用二项式分布更简单,但需要满足一个前提。
假如我们要计算一个二项式分布概率,n为3000,用二项式分布的公式需要计算3000!,这个数字太大,很难计算出来。此时我们要用泊松分布来求解近似答案。
我们来看一下泊松分布和二项式分布的期望方差对比
泊松分布 E(X) =λ,Var(X) = λ
二项式分布: E(X) = np,Var(X) =npq
我们要找出泊松分布与二项式分布的期望和方差近似相等的情况,因为泊松分布的期望和方差相等,所以np 要近似 npq
当q近似等于1且n很大时,np和npq近似相等。因此:
当n很大p很小时,可以用泊松分布X~Po(np)近似代替二项式分布X~B(n,p)
标准:当n>50且p<0.1时,为典型近似情况。
例题:一个学生要参加一场考试,但他没有做任何复习。他需要猜测每一题的答案,每一题的答答对概率是0.05。考卷上共有50个问题,他答对5题的概率是多少?用二项式分布的泊松分布近似法求解。
λ =np =50 x 0.05 =2.5
P(X =5) = e^-2.5 x 2.5^5 / 5!
= e^-2.5 x 97.65625 / 120 =0.067
总结
泊松分布的概率、期望、方差计算
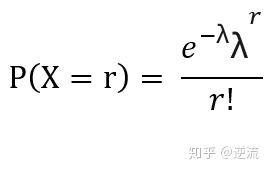
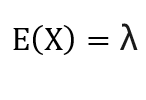
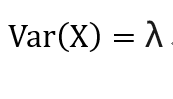
泊松分布随机变量的组合
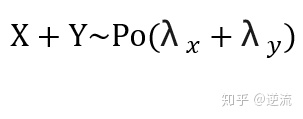
泊松分布与二项式分布的关系
如果X~B(n,p),当n较大而p较小时,X可以近似表示为:
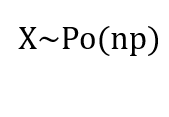
本文归纳总结参考《深入浅出统计学》