1. 模型准备：二阶传递函数模型

1.1 二阶传递函数模型

1.1.1 时域模型

1.1.2 频域模型

1.2 二阶传递函数公式和参数

$$G(s)=\frac{K{e}^{-T_{d}s}{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$$

此时传递函数为：
$$G(s)=\frac{0.0720571\ast 0.893308^2}{s^2+2\ast 1.378866\ast 0.893308s+0.893308^2}$$
即：
$$G(s)=\frac{0.0575}{s^2+2.4635s+0.7980}$$

2. 开始建模：在simulink中搭建二阶传递函数模型

2.1 从simulink库中添加传递函数模块

打开MATLAB，在命令行里输入：

simulink

启动simulink。

新建一个空白的文件，然后打开Simulink Library Browser，点击左侧目录Simulink/Continous：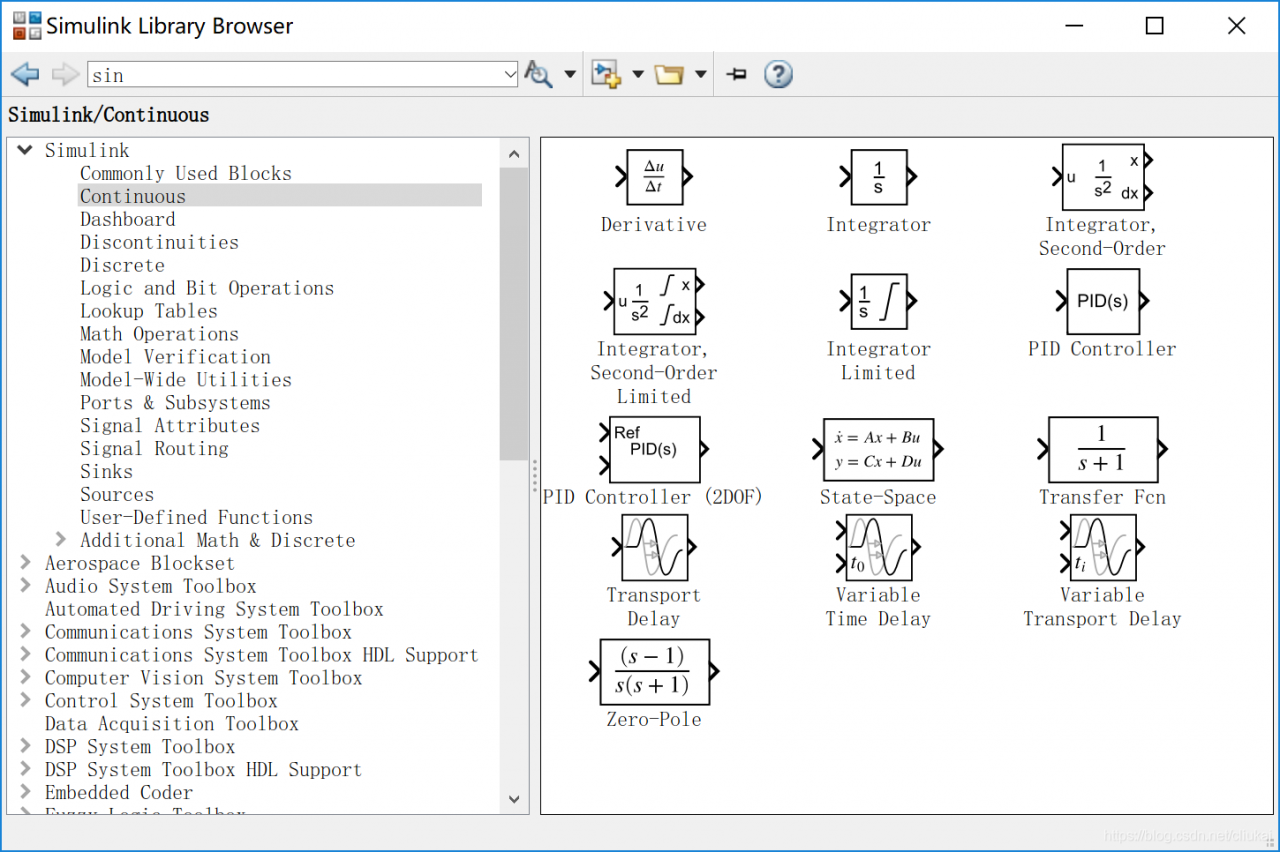

将Transfer Fcn拖拽到工作空间中

2.2 设置传递函数参数

双击该模块，根据传递函数的参数进行设置
$$G(s)=\frac{0.0575}{s^2+2.4635s+0.7980}$$

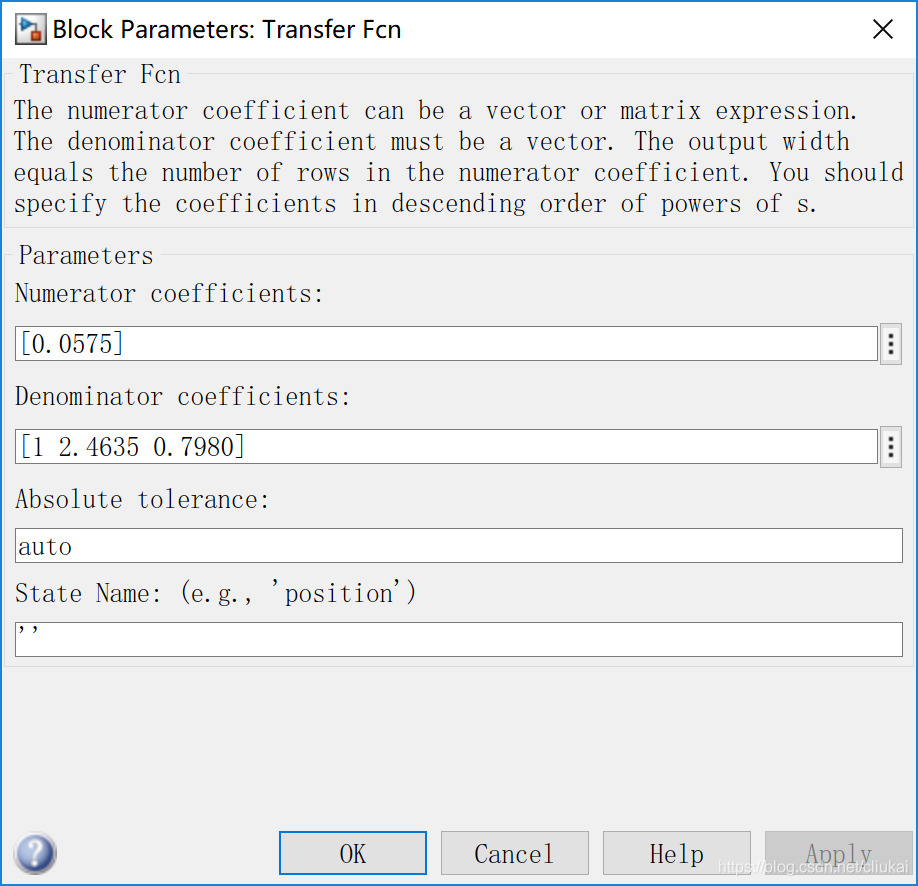
• Numerator中填入分子的系数[0.0575]

• Denominator中填入分母的系数[1 2.4635 0.7980]

确认应用：

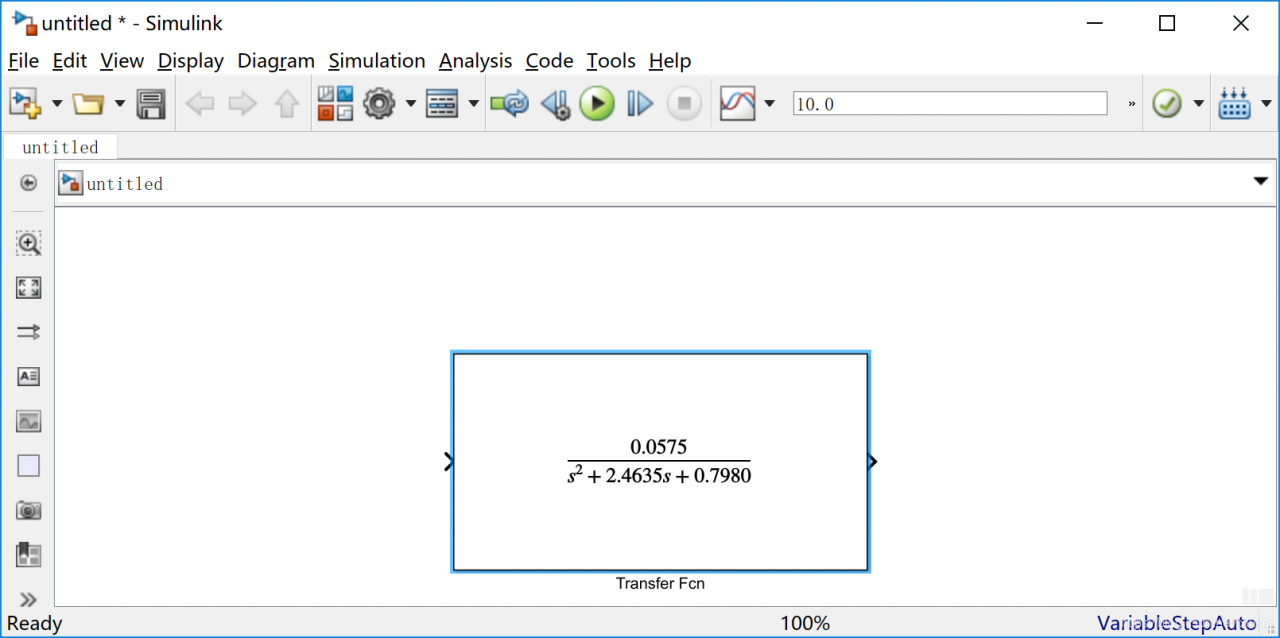
2.3 添加输入和输出组件

• 在Source中分别添加阶跃响应，正弦等信号发生器到输入
• 在Sink中添加若干个Scope到输出
• 然后搜索switch，添加两个开关，便于观察
• 在信号发生器到示波器中间添加一个Gain，适当调整大小到0.01便于在一个示波器中观察两个波形

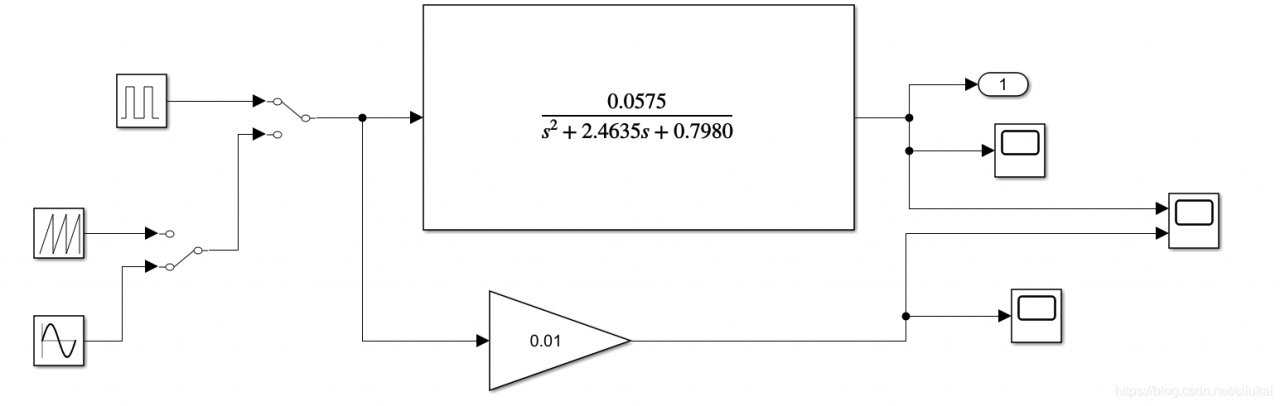
2.4 运行模型，并使用示波器查看

切换输入源为阶跃响应，然后双击示波器，点击运行按钮，观察波形

说明：蓝色为原始信号（缩小了100倍），黄色为经过传递函数之后的输出信号

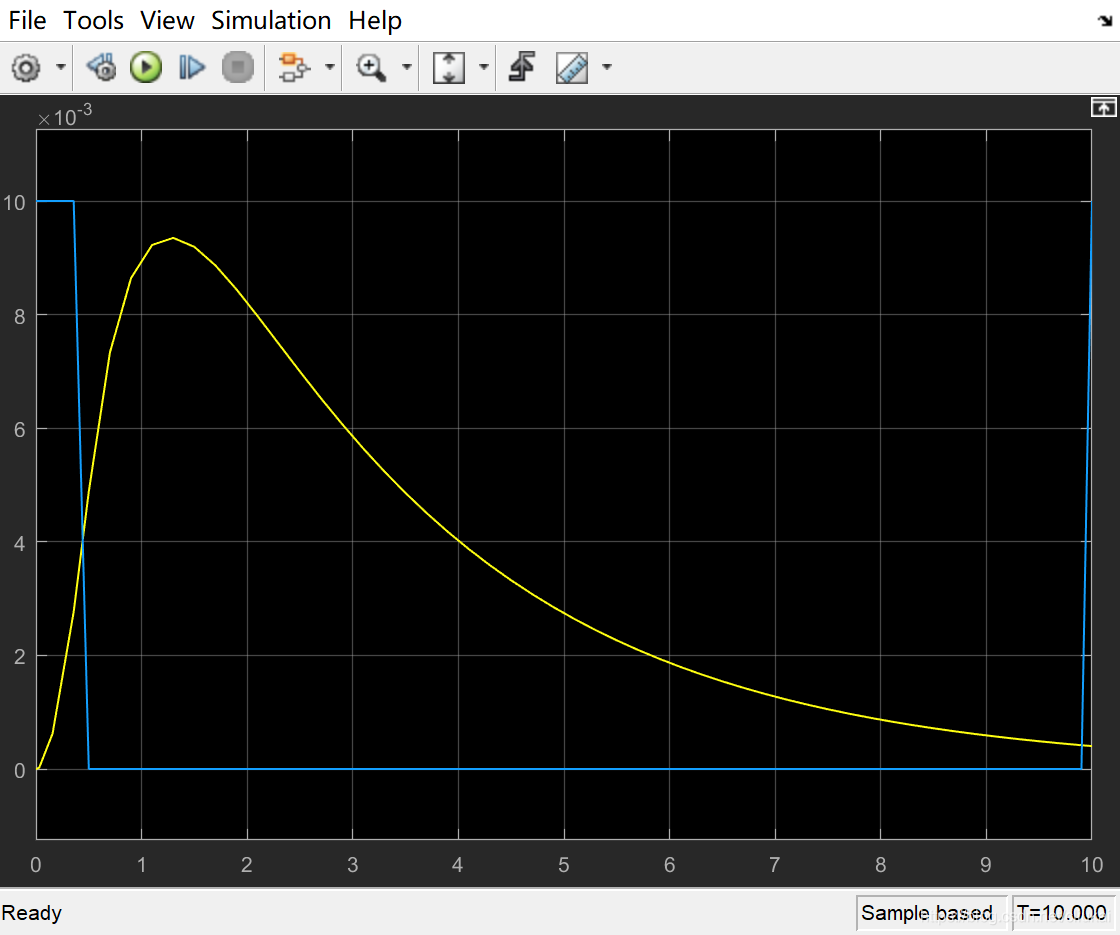
双击开关，切换一组输入源为正弦波，将时间调整为30s，继续观察

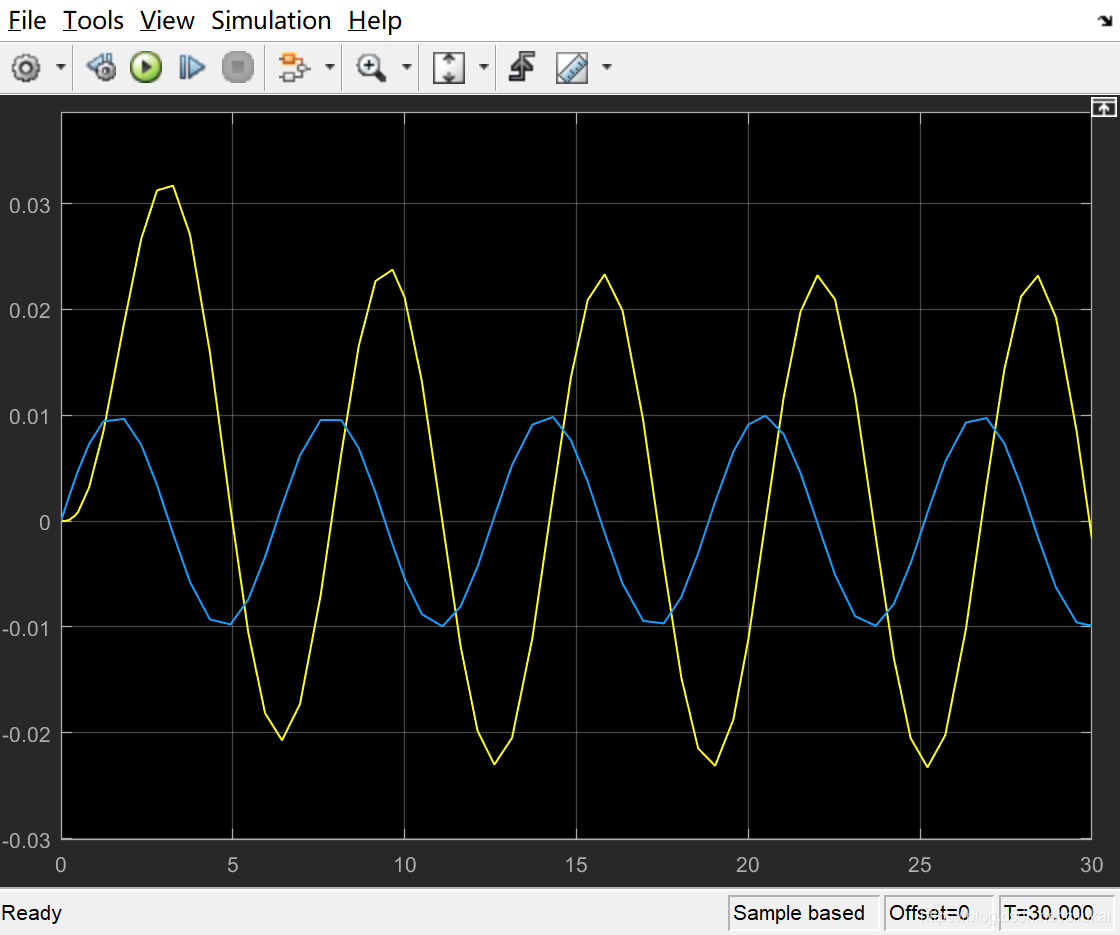
3. 参考文献

1. 通过传递函数为线性系统建模 - Simulink - MathWorks 中国
   https://ww2.mathworks.cn/help/simulink/slref/transferfcn.html

2. Model linear system by transfer function - Simulink - MathWorks China
   https://ww2.mathworks.cn/help/simulink/slref/transferfcn.html?lang=en