必会的排序算法及代码实现

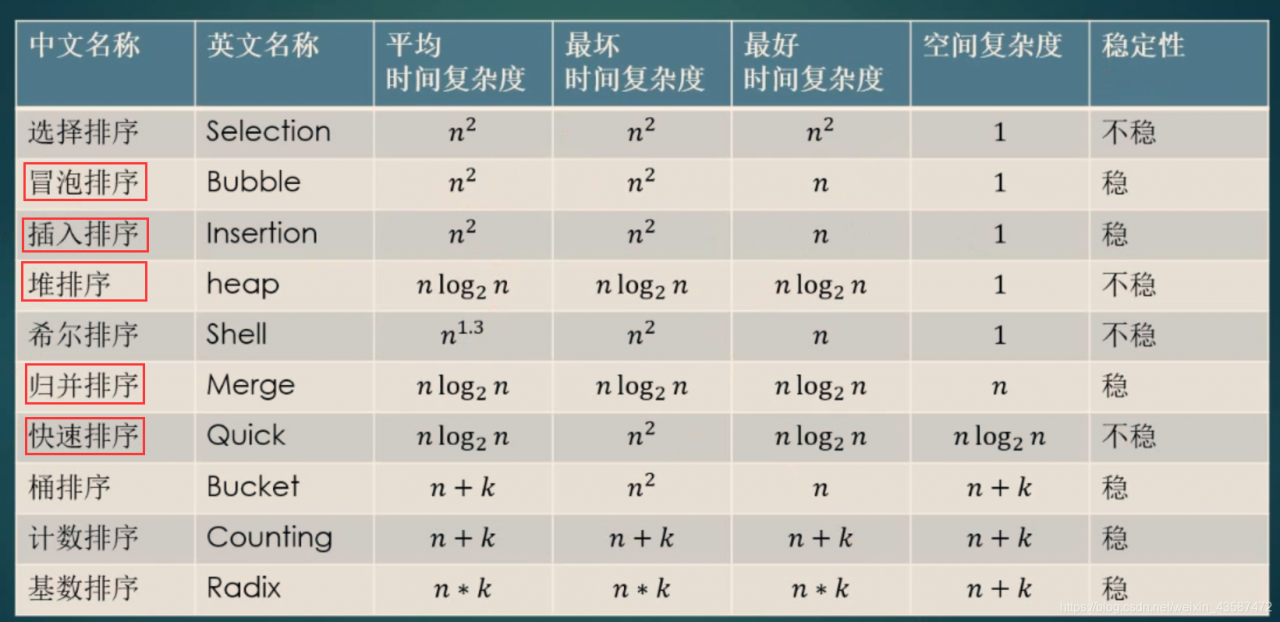
标红的比较重要！至少要记住这几个！

简单排序：

	//公共方法
    static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    static void print(int[] arr){
    	for (int i=0;i<arr.length ;i++) {
    		System.out.print(arr[i] + " ");
    	}
    }

冒泡排序

冒泡排序：从数组的第一个位置开始，比较相邻的两个元素，如果前一个元素比后一个大（或小），就交换两者位置，依次比较，遍历一遍就能找到数组中最大（最小）的元素，这样遍历后数组最后一个元素是最大（最小）的，下一次遍历就从头到 == len(array) -j== 就可以了（ j 表示第 j 趟遍历）。
这样每一趟遍历就能找到数组剩余元素中最大（最小）的一个，n-1 趟后数组就有序了。

public class BubbleSort {
    public static void main(String[] args) {
        int[] arr= {1,5,3,9,8,4,2,6,7};
        sort(arr);
        print(arr);
    }

    static void sort(int[] arr){
    	for (int i = arr.length-1; i > 0; i--) {
    		for (int j = 0; j < i; j++ ) {
	    		if (arr[j] > arr[j + 1]) {
	    			swap(arr, j, j + 1);
	    		}
    		}
    	}
    }
}

python版：

def bubbleSort(arr):
    count = 0
    n=len(arr)
    for j in range(n-1):   # 外循环控制遍历的次数,n个数除去第一个数剩n-1个数，最多遍历n-1次
        for i in range(n-1-j): # 内循环控制遍历到哪一位
            if arr[i]>arr[i+1]:
                arr[i],arr[i+1]=arr[i+1],arr[i]
                count+=1
        if count==0:    #数列本身有序
            return lst
    return lst
print(bubbleSort(lst))

插入排序（增量策略）：

算法复杂度为O(n^2)

在基本有序的序列中最好用。

插入排序的核心在于，它把一个无序数列看成两个数列，假如第一个元素构成了第一个数列，那么余下的元素构成了第二个数列，
很显然，第一个数列是有序的，那么我们把第二个数列的第一个元素拿出来
从右向左依次和第一个数列的数比较，遇到比自己大的就交换，比自己小的就插入到第一个数列，
使它依然构成一个有序数列，直到第二个数列中的所有元素全部插入到第一个数列，这时候就排好序了。

public class InsertSort {
    public static void main(String[] args) {
        int[] arr= {1,5,3,9,8,4,2,6,7};
        sort(arr);
        print(arr);
    }

    static void sort(int[] arr){
    	for (int i = 1; i < arr.length; i++) {
    		for (int j = i; j > 0; j--) {
	    		if (arr[j] < arr[j - 1]) {
	    			swap(arr, j, j - 1);
	    		}
    		}
    	}
    }
}

python版:

lst=[5,7,1,3,6,2,4]
def insertSort(arr):
    for i in range(1,len(arr)):
        j=i-1
        key=arr[i]
        while j>=0:
            if arr[j]>key:
                arr[j + 1]=arr[j] #向后移
                arr[j]=key
                # arr[j+1],arr[j]=arr[j],arr[i]
            j-=1
    return arr
print(insertSort(lst))

快速排序 (分治策略)

递归实现
平均算法复杂度为O(nlogn)，最坏为n方

public class QuickSortDemo{
	public void sort(int [] arr, int left, int right){
		int p;
		if (left < right) {
			p = quickSort(arr, left, right);
			sort(arr, left, p - 1);
			sort(arr, left+1, right);
		}
		public int quickSort(int [] arr, int left, int right){
			int pivot = arr[left];
			while(left < right){
				while(left<right && privot <= arr[right]){
					right--;
				}
				arr[left] == arr[right];
				while(left<right && privot >= arr[left]){
					left++;
				}
				arr[right] = arr[left];
			}
			arr[left] = privot;
			return left;
		}
	}
}

python版：

lst1=[5,7,1,3,6,2,4]
# l,r 分别代表序列最小下标值和最大下标值
def quickSort(arr,l,r):
    if l>=r:
        return arr
    key=arr[l]
    low=l
    high=r
    while l<r:
        while l<r and arr[r]>=key:
            r-=1    #大于等于基准值时继续往左查找
        arr[l]=arr[r] #小于基准值时就交换位置
        while l<r and arr[l]<=key:
            l+=1    #小于等于基准值时继续往右查找
        arr[r]=arr[l]   #大于基准值时就交换位置
    arr[l]=key  # l=r时即左右下标指向同一个数说明序列已经遍历一遍，
    # 这个位置就是一个分界（左边都是小于基准值的，右边都是大于基准值的），故令arr[l]=key
    # 再对前面步骤将序列分成的两子部分进行迭代排序
    quickSort(arr,low,l-1)
    quickSort(arr,l+1,high)

quickSort(lst1,0,6)
print(lst1)

二分归并排序(分治策略)

算法复杂度为O(nlogn)

python版：

def merge(a,b):
    c=[]
    h=j=0
    while j<len(a) and h<len(b):
        if a[j]<b[h]:
            c.append(a[j])
            j+=1
        else:
            c.append(b[h])
            h+=1
    if j==len(a):
        for i in b[h:]:
            c.append(i)
    else:
        for i in a[j:]:
            c.append(i)
    return c
def mergeSort(arr):
    if len(arr)<=1:
        return arr
    middle=len(arr)//2
    left=mergeSort(arr[:middle])
    right=mergeSort(arr[middle:])
    return merge(left,right)

lst2=[5,7,1,3,6,2,4]
print(mergeSort(lst2))