一 问题描述

由于大部分道路在战争期间已被完全摧毁，所以两个城市之间可能没有路径，也没有环。已知道路状态，想知道任意两个城市之间是否存在路径。若答案是肯定的，则输出它们之间的最大距离。

二 输入

输入包含多个测试用例。每个测试用例第 1 行包含 3 个整数 n、m、c，n 表示城市数。编号为 1 到 n，接下来的 m 行，每行包含三个整数，i、j、k，表示城市 i 和城市 j 之间的道路，长度为 k，最后 c 行，每行包含 i、j 两个整数，表示查询城市 i 和城市 j 之间的最短路径。

三 输出

对于每个查询，若两个城市之间没有路径，则输出“Not connected”，否则输出它们之间的最短路径。

四 输入和输出样例

1 输入样例

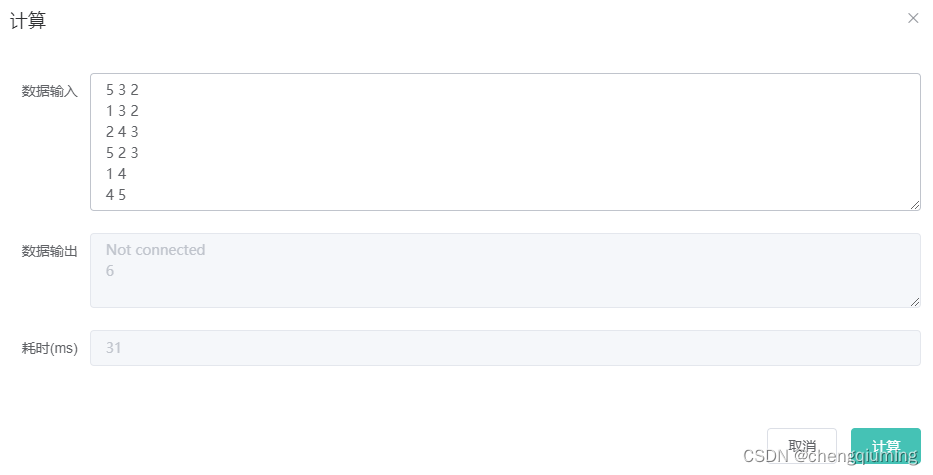
5 3 2

1 3 2

2 4 3

5 2 3

1 4

4 5

2 输出样例

Not connected

6

五 分析

本问题的两点之间无环，且有可能不连通，有可能不是一棵树，而是由多棵树组成的森林。因此需要判断是否在同一棵树中，若不在同一棵树中，则输出 Not connected，否则可以使用求解最近公共祖先的 Tarjan 算法求解。

六 设计

1 根据输入的数据，采用链式前向星存储图。

2 采用 Targan 算法离线处理所有查询，因为本问题的操作对象可能有多棵树，因此需要注意两个问题：

a 修改 Targan 算法，引入一个 root 参数，用来判断待查询的两个节点是否在同一棵树中。

b 对未访问过的节点再次执行 Targan 算法。

3 将每个查询的两个节点之间的距离都存储在答案数组中。

七 代码

package com.platform.modules.alg.hdu2874;

public class Hdu2874 {
    private final int maxn = 10000;
    private final int maxq = 1000000;
    Node e[] = new Node[2 * maxn];
    Query qe[] = new Query[2 * maxq];

    int ehead[] = new int[maxn];
    int dis[] = new int[maxn];
    int fa[] = new int[maxn];
    int ecnt;
    int vis[] = new int[maxn];

    int qhead[] = new int[maxn];
    int ans[] = new int[maxq];
    int qcnt;
    int n, m, c;


    void init() {
        ecnt = qcnt = 0;
        ehead = new int[maxn];
        for (int i = 0; i < ehead.length; i++) {
            ehead[i] = -1;
        }
        qhead = new int[maxn];
        for (int i = 0; i < qhead.length; i++) {
            qhead[i] = -1;
        }

        vis = new int[maxn];
        for (int i = 0; i < vis.length; i++) {
            vis[i] = -1;
        }

        for (int i = 0; i < e.length; i++) {
            e[i] = new Node();
        }

        for (int i = 0; i < qe.length; i++) {
            qe[i] = new Query();
        }
    }

    void add1(int u, int v, int w) {
        e[ecnt].to = v;
        e[ecnt].w = w;
        e[ecnt].next = ehead[u];
        ehead[u] = ecnt++;
    }

    void add2(int u, int v, int id) {
        qe[qcnt].id = id;
        qe[qcnt].to = v;
        qe[qcnt].next = qhead[u];
        qhead[u] = qcnt++;
    }

    int Find(int x) {
        if (x != fa[x])
            fa[x] = Find(fa[x]);
        return fa[x];
    }

    void LCA(int u, int deep, int root) {
        fa[u] = u;
        dis[u] = deep;
        vis[u] = root;
        for (int i = ehead[u]; i != -1; i = e[i].next) {
            int v = e[i].to;
            if (vis[v] == -1) {
                LCA(v, deep + e[i].w, root);
                fa[v] = u;
            }
        }
        for (int i = qhead[u]; i != -1; i = qe[i].next) {
            int v = qe[i].to;
            if (vis[v] == root)
                ans[qe[i].id] = dis[v] + dis[u] - 2 * dis[Find(v)];
        }
    }

    public String output = "";

    public String cal(String input) {
        String[] line = input.split("\n");
        String[] word = line[0].split(" ");
        n = Integer.parseInt(word[0]);
        m = Integer.parseInt(word[1]);
        c = Integer.parseInt(word[2]);

        int u, v, w;
        init();

        for (int i = 1; i <= m; i++) {
            String[] info = line[i].split(" ");
            u = Integer.parseInt(info[0]);
            v = Integer.parseInt(info[1]);
            w = Integer.parseInt(info[2]);
            add1(u, v, w);
            add1(v, u, w);
        }

        for (int i = 0; i < c; i++) {
            String[] query = line[i + m + 1].split(" ");
            u = Integer.parseInt(query[0]);
            v = Integer.parseInt(query[1]);
            ans[i] = -1;
            add2(u, v, i);
            add2(v, u, i);
        }
        for (int i = 1; i <= n; i++) {
            if (vis[i] == -1)
                LCA(i, 0, i);
        }
        for (int i = 0; i < c; i++) {
            if (ans[i] == -1) output += "Not connected\n";
            else output += ans[i] + "\n";
        }

        return output;
    }
}

// 边
class Node {
    public int to; // 邻接点
    public int w; // 边权
    public int next; // 下一条边的下标
}

class Query {
    public int to;
    public int id; // 查询的编号
    public int next;
}

 八 测试