模型前的铺垫
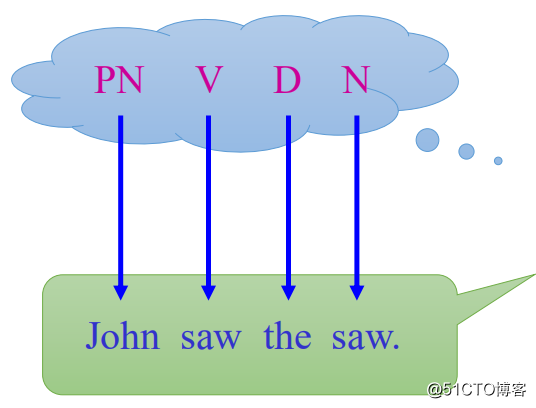
我们先引入一个假设，假设一个句子的产生只需要两步：
第一步：基于语法产生一个合乎文法的词性序列
第二步：对第一步产生的序列中的每个词性找到符合这个词性的一个词汇，从而产生一个词汇序列，便产生出了一个句子
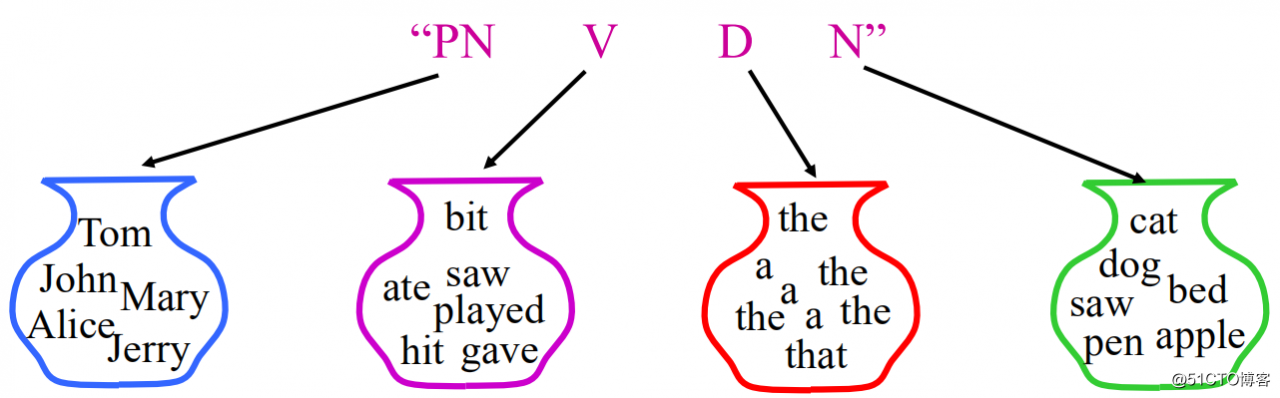
图1
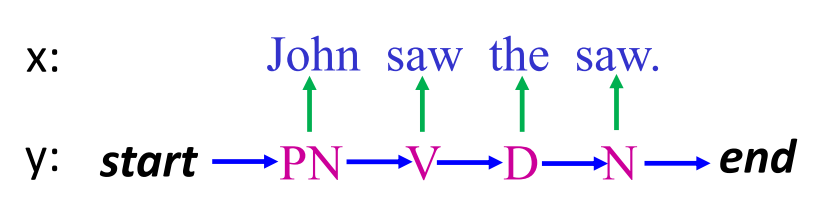
那么如图1所示，假如我们基于语法产生了一个词性序列("PN V D N")，那基于这样的词性序列到对应的词典集合中选词便可以组合出一个句子。
图2
假如我们产生的句子是"John saw the saw",那么如图2所示，每个词都有一定的概率被选出，基于词性序列("PN V D N")产生这个句子的概率为：
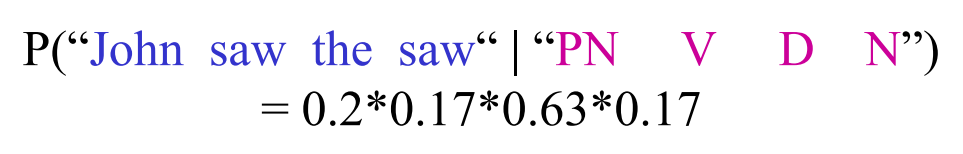
如果把词性序列用y表示，把句子的词汇序列用x表示，那么上述句子的生成可以表示为：
这样我们就可以得到序列x、y同时出现的概率P(x,y)：
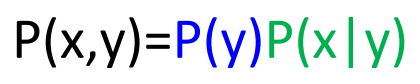
其中P(y)表示序列y出现的概率:
P(x|y)表示基于序列y生成序列x的概率:
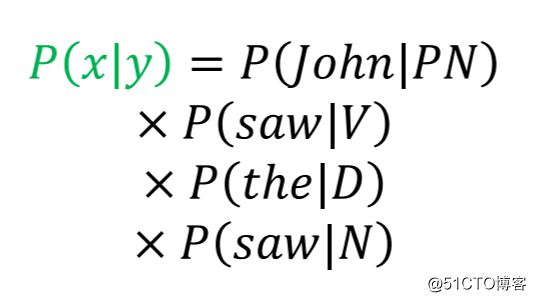
基于上述想法，我们可以得到更一般化的表示：
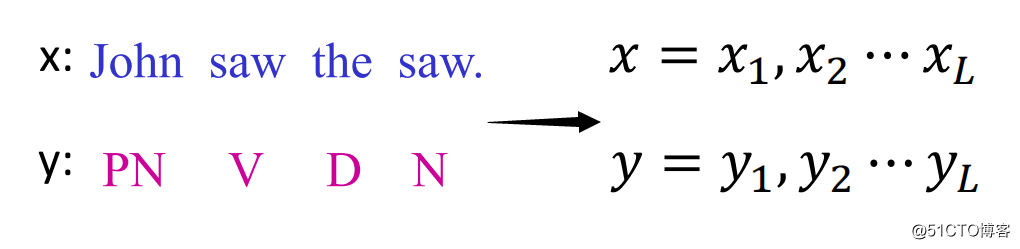
从而P(y)可以更一般的表示为：
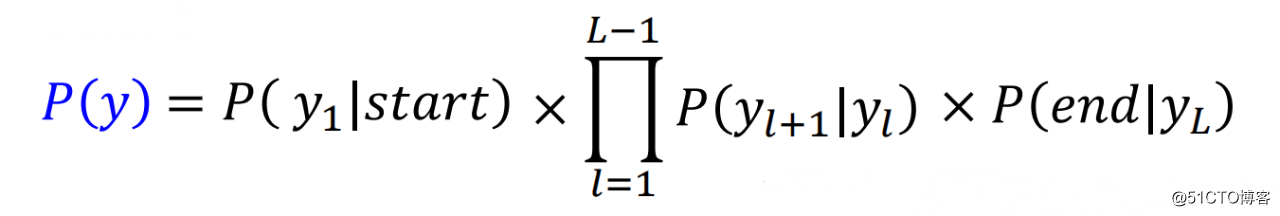
同样P(x|y)可以更一般的表示为：
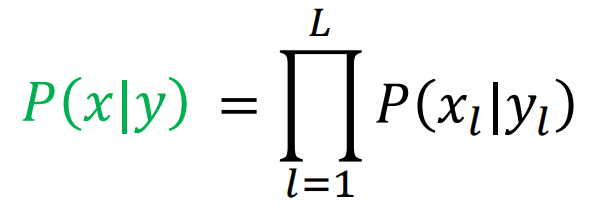
那么可以得到P(x,y)更一般的表示为：
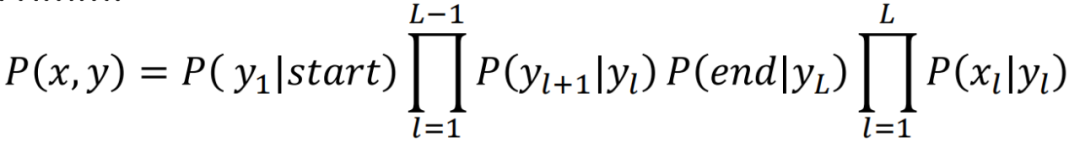
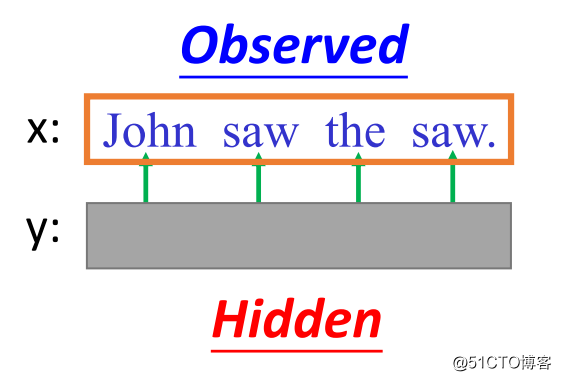
图3
再来看图3，当序列x是已知的或者说是可观测的，而标记序列y是隐藏的或者说是未知的，那么如何来求得理想标记序列y呢？我们通过采取求解条件概率P(y|x)来求得，即：
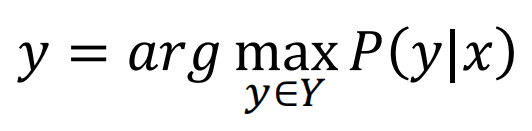
其中y是一个可能的标记序列，Y是所有可能的标记序列。上式的意义在于期望求得一个能使条件概率P(y|x)最大的标记序列y。也就是说，如果我知道了P(y|x)如何求，再把每个可能的标记序列y带进去，就能得到想要求得的理想标记序列y。
CRF模型引入
基于上述的铺垫，下面我们开始引入条件随机场模型。
条件随机场(CRF)模型可以用如下式子来描述：
其中：w表示权重向量
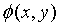表示特征向量
现在我们重点来关注如何求解条件概率P(y|x)辅助理解
从标注问题的角度来理解条件概率P(y|x)的含义。x表示给定的待标注序列，y表示给定x下对应的一个标记序列。我们希望通过求解条件概率P(y|x)来得到给定x条件下对应的一个理想标注序列
P(y|x)可以表示为：
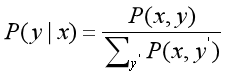
我们知道
不妨设
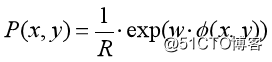辅助理解
R为比例系数
将上式带入P(y|x)的表达式中可得
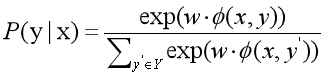辅助理解
Y表示所有可能的标注序列的集合，y'表示所有标注序列的集合中的某个标注序列
观察上式，可以看到分母部分其实只和x有关，所以可以将其简化的表示为Z(x)，即：
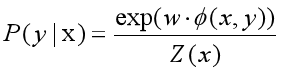
也就是说，要求P(y|x)，关键在于求解P(x,y)，由之前的铺垫，我们知道：
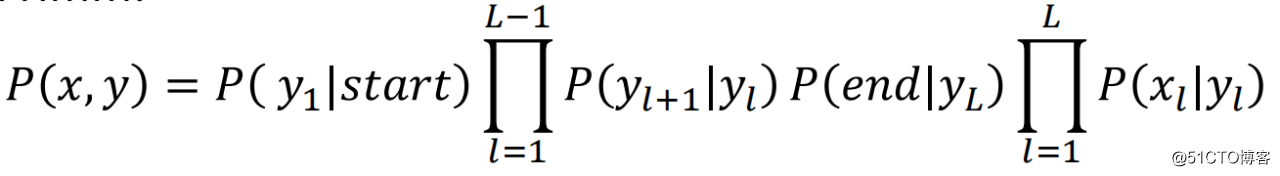
我们对上式两边取对数得：
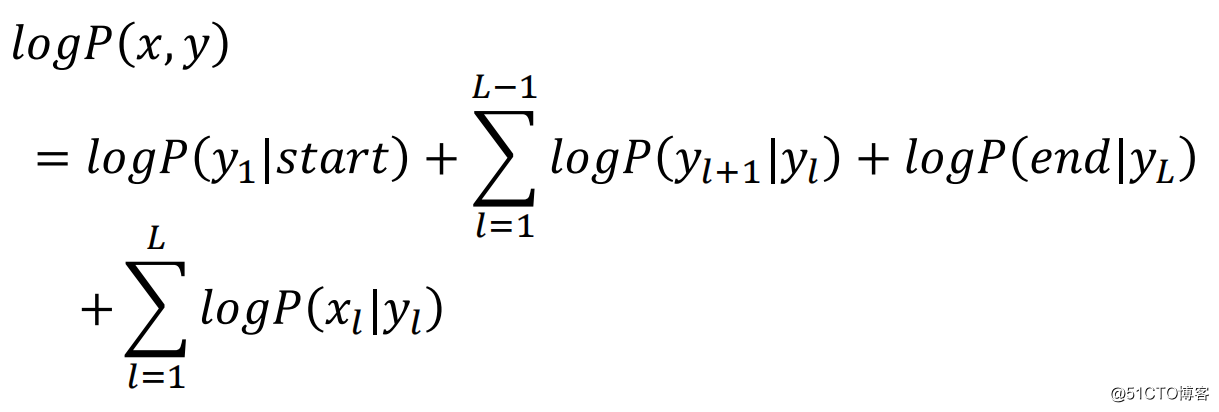
其中
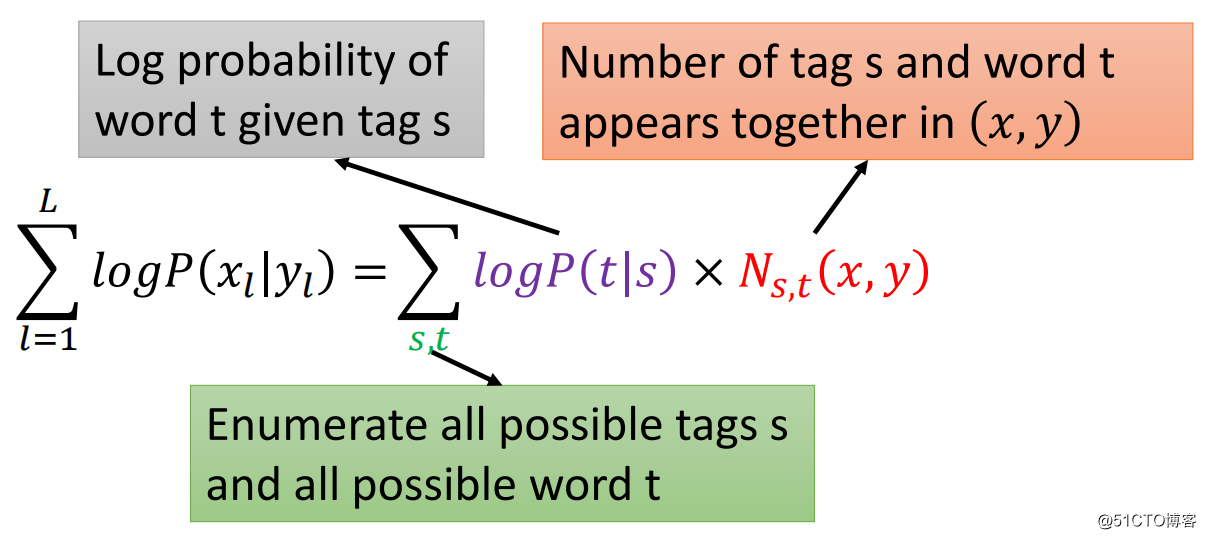
上式是如何来的呢？
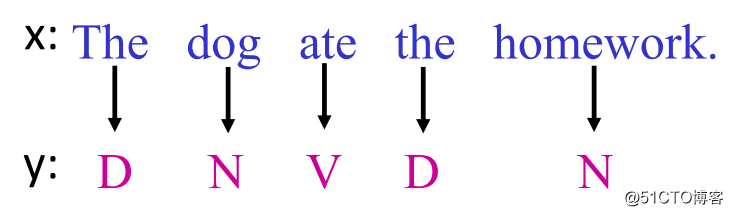
图4
如图4所示，可得：
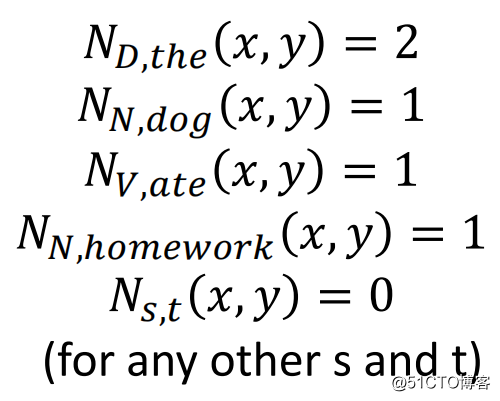
从而
同样，我们也能得到
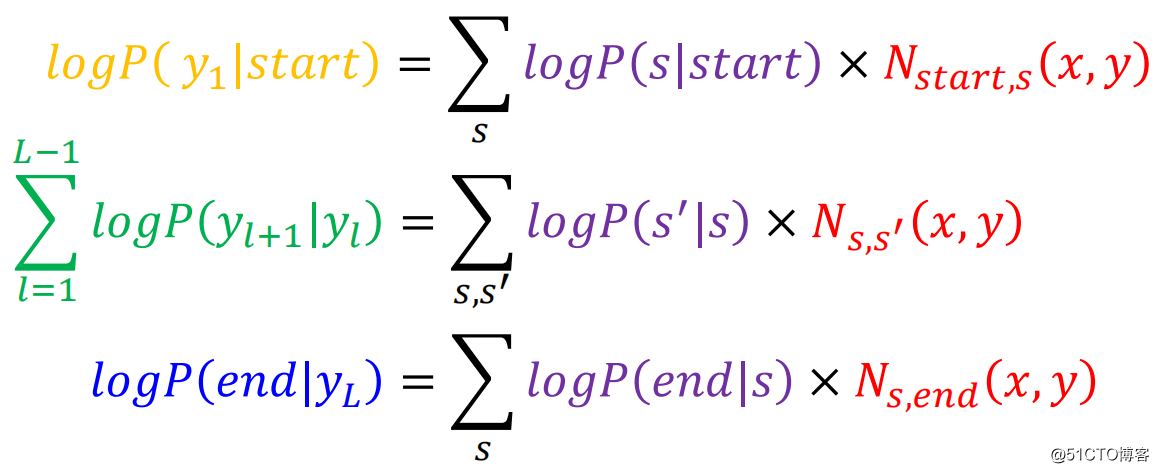
从而
我们可以将上式向量化表示为：
我们可以令
其中
由于
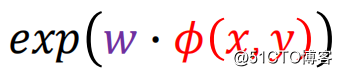的值可能会大于1，这就不能用来表示概率了，所以
参考资料：
李宏毅《Sequence Labeling Problem》课程
目前本公众号建立了一个技术交流群
诚挚欢迎各位志同道合的朋友加入
