混合型数据的邻域条件互信息熵属性约简算法
兰海波
中国气象局公共气象服务中心
摘要：属性约简是粗糙集理论的重要研究内容之一，其主要目的是消除信息系统中不相关的属性，降低数据维度并提高数据知识发现性能。然而，基于粗糙集的属性约简方法大多没有考虑属性之间的依赖性，使得最终的属性约简结果存在一定的冗余属性。对此，提出一种基于邻域条件互信息熵的属性约简算法。首先，在传统邻域熵的基础上，针对混合型数据，提出混合型邻域互信息熵模型和混合型邻域条件互信息熵模型；然后利用这两种熵模型进行混合型信息系统的属性依赖度评估和属性启发式搜索，并设计出一种属性约简算法；最后通过UCI数据集的实验分析，证明了提出的算法具有较高的属性约简性能。
关键词： 粗糙集 ; 属性约简 ; 邻域 ; 互信息熵 ; 条件互信息熵
论文引用格式：
兰海波. 混合型数据的邻域条件互信息熵属性约简算法[J]. 大数据, 2022, 8(4): 133-144.
LAN H B. Neighborhood conditional mutual information entropy attribute reduction algorithm for hybrid data[J]. Big Data Research, 2022, 8(4): 133-144.
0 引言
在大数据应用情景下，具有噪声、无关或冗余特征的数据集对数据挖掘、知识发现和模式识别产生了巨大的挑战。如何从数据集所有属性中选择出最优属性子集是各种学习任务的重要研究课题。属性约简是粗糙集理论的重要研究分支，其主要目的是消除信息系统中不相关的属性，降低数据维度并提高数据知识发现性能。
基于粗糙集理论，学者们提出了多种属性约简算法。例如，Hu Q H等人基于邻域粗糙集，将邻域依赖度作为数值型信息系统的属性评估，提出一种属性约简算法；Pang Q Q等人提出一种基于邻域区分度的半监督属性约简算法；在Pang Q Q等人的基础上，Hu M等人在邻域粗糙集下提出权重邻域依赖度，并构造一种改进的属性约简算法；Shu W H等人对邻域粗糙集进行增量式构造，提出一种高效的增量式属性约简算法；盛魁等人对邻域区分度进行增量式构造，提出一种新的属性约简算法；姚晟等人将这些属性约简算法进一步拓展，提出非平衡数据下不完备混合型信息系统的属性约简算法。另外，部分学者采用其他类型的粗糙集模型进行属性约简算法的设计，例如，Wang C Z等人在模糊粗糙集下提出自信息，并进行属性约简算法的设计；Yuan Z等人利用模糊粗糙集提出混合型数据的非监督属性约简算法；栾雨雨等人利用混沌离散粒子群提出一种新的粗糙集属性约简算法；Hu M等人利用K近邻粗糙集模型提出一种新颖的属性约简算法；桑彬彬等人利用优势粗糙集构造出一种属性约简算法。
利用互信息熵进行属性约简近年来受到了学者们越来越多的关注。熊菊霞等人提出邻域互信息熵的混合型数据属性约简算法，陈帅等人提出邻域互补信息度量的属性约简算法，姚晟等人提出邻域互信息熵的非单调性属性约简算法。然而，这些属性约简算法大多没有考虑属性之间的相互作用，即在进行属性约简的搜索过程中，选择重要度高的属性作为候选属性，而没有考虑所选属性的独立性，新选择的属性与已有的属性可能存在一定的依赖关系，这使得最终的属性约简结果可能存在一定的冗余性。互信息熵与条件互信息熵是评估随机变量独立性的一种重要度量方法，本文将利用这两种度量方法提出一种新的属性约简算法。同时，实际应用环境下的数据集往往是数值型和离散型混合类型，例如对于医疗信息系统，患者的性别、听觉、视觉、嗅觉等都是离散型的属性，身高、体重和血液检查中各种酶的指标都是数值型的属性，因此本文将研究混合型信息系统下的属性约简问题。
首先，本文在邻域粗糙集模型的基础上，构造出混合型信息系统下的邻域信息熵模型，并进一步提出混合型邻域互信息熵模型和混合型邻域条件互信息熵模型；然后，将提出的混合型邻域互信息熵和混合型邻域条件互信息熵用于混合型信息系统属性之间的相关性度量；最后，将这两种熵度量作为启发式函数设计出一种属性约简算法，并通过6个UCI数据集的属性约简实验，证明了本文的属性约简算法通过考虑属性之间的依赖性可以提高约简结果的分类性能，同时本文算法也具有较小的属性约简耗时。
1 基本理论
将邻域信息系统 表示为二元组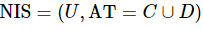
，其中，
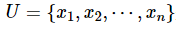是一个非空有限对象或样本的集合，称之为论域；
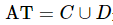是一个非空有限属性或特征的集合，称之为属性全集，其包含两个部分，分别称之为条件属性集C 和决策属性集D。
在邻域信息系统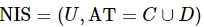
中，通常使用距离度量来评估信息系统中对象之间的相似性，对于属性子集
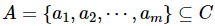，对象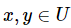
的距离度量一般被定义为：
其中，ai(x)表示对象x在属性ai下的属性值，ai(y)表示对象 y在属性ai下的属性值，λ的取值范围一般为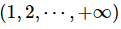
。基于该度量函数，可以在邻域信息系统下构造出邻域关系。
定义1：设邻域信息系统表示为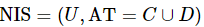
，则属性子集
确定的邻域关系如下。
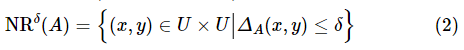
其中，δ被称为邻域关系的邻域半径。邻域关系满足自反性和对称性，但不一定满足传递性。利用邻域关系可以得到邻域信息系统中每个对象的邻域类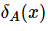
：
定义2 ：设邻域信息系统表示为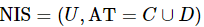
，属性子集
确定的邻域关系为
，则对象集
在邻域关系
下的邻域下近似集
和邻域上近似集
分别定义如下。
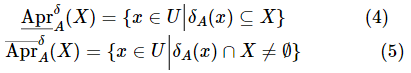
信息熵模型是评估信息系统不确定性的一种重要方法，Hu Q H等人在邻域信息系统下提出了一种邻域熵模型。
定义3：设邻域信息系统表示为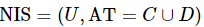
，属性子集
确定的邻域关系为
，对象 x∈U 在
下的邻域类为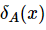
，那么邻域关系
确定的邻域熵
定义如下。
Hu Q H等人提出的邻域熵模型在邻域粗糙集的不确定性度量和属性约简方面发挥了重要作用，使得邻域熵模型成为邻域粗糙集的重要研究内容。
2 混合型信息系统的邻域条件互信息熵模型
然而，实际应用中的数据包含数值型和标记型，传统的邻域粗糙集模型仅适用于数值型，针对这一局限性，盛魁等人提出了基于混合型信息系统的邻域粗糙集模型。
定义4：设混合型信息系统表示为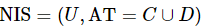
，其中C=Cn∪Cm且Cn∩Cm=∅，Cn 为条件属性集中的数值型属性子集，Cm 为条件属性集中的标记型属性子集。对于 A=An∪Am，其中An⊆Cn、Am⊆Cm，那么A⊆C确定的混合邻域关系如下。
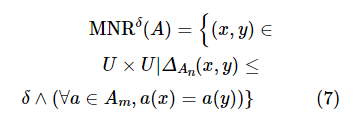
同时，对于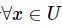
，在混合邻域关系
下的邻域类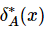
定义为：
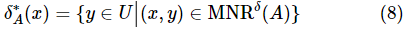
基于混合信息系统的混合邻域关系和邻域类，盛魁等人进一步提出了一种改进的邻域粗糙集模型。
定义5：设混合型信息系统表示为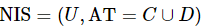
，A=An∪Am确定的混合邻域关系为
，那么对象集
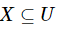在
下的邻域下近似集
和邻域上近似集分别定义如下。
在盛魁等人提出的混合型信息系统邻域粗糙集基础上，下面将进一步提出混合信息系统的邻域熵、邻域联合熵、邻域条件熵以及邻域条件互信息熵模型等，进一步完善邻域粗糙集模型下的信息熵理论。
定义6：设混合型信息系统表示为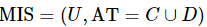
， A=An∪Am确定的混合邻域关系为
，对象x∈U在
下的邻域类为
，那么混合邻域关系
确定的混合邻域熵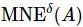
定义如下
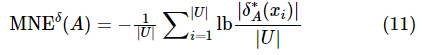
其中，对象xi的邻域不确定性构成了对象集的邻域熵（即平均不确定性），定义为
。
定义7：设混合型信息系统表示为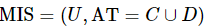
，属性子集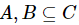
，那么A和B的混合邻域联合熵定义如下。
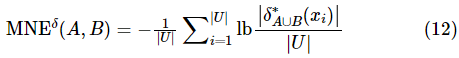
定义8：设混合型信息系统表示为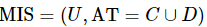
，属性子集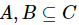
，那么B关于A的混合邻域条件熵定义如下。
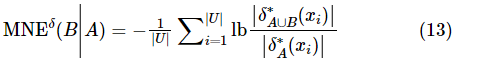
根据定义6~定义8，混合邻域条件熵具有如下性质。
性质1：设混合型信息系统表示为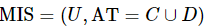
，属性子集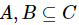
，那么可以得到式（14）。
证明：根据定义6和定义7，可以得到式（15）。
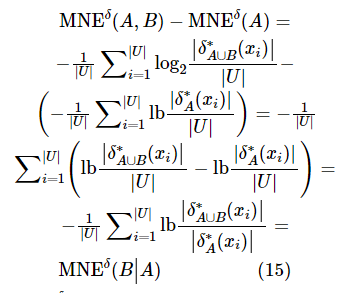
则
成立。
定义8中的混合邻域条件熵与信息论中的条件熵类似，反映了引入属性子集A后B中剩余的不确定性量，混合邻域条件熵可以通过A和B的联合不确定性与A的不确定性来计算。
定义9：设混合型信息系统表示为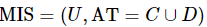
，属性子集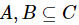
，那么A和B的混合邻域互信息熵定义为如下。
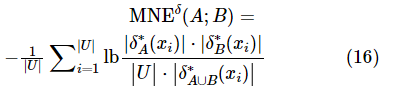
混合邻域熵、混合邻域条件熵和混合邻域互信息熵具有如下关系。
性质2：设混合型信息系统表示为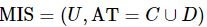
，属性子集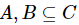
，那么可以得到如下计算式。
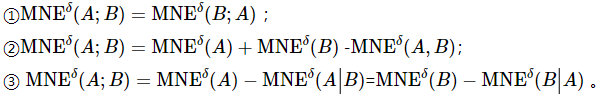
证明：根据定义9，可以得到式（17）。
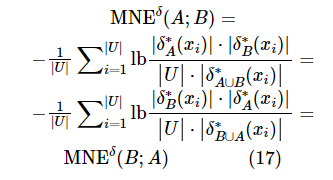
则①成立。
根据定义6和定义7可以得到：
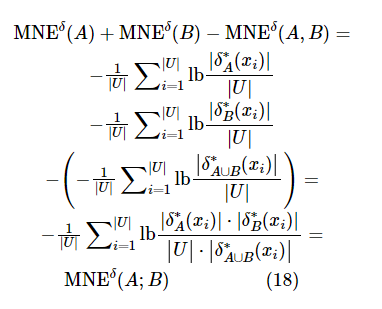
则②成立。
根据定义6和定义8可以得到：
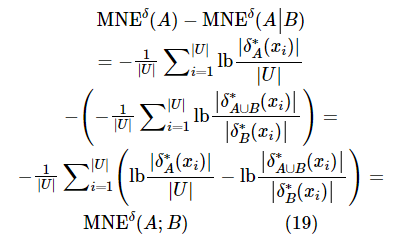
同理，可以得到：
则③成立。
通过性质2可以看出属性子集A和B的互信息量与B和A的互信息量是一致的。属性子集A和B混合邻域互信息熵可以表示为各自的混合邻域熵值去除A和B后的混合邻域联合熵值。
与信息论理论类似，接下来进一步提出混合邻域条件互信息熵。
定义10：设混合型信息系统表示为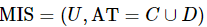
，属 性 子 集 A1,A2, 
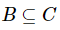，那么在属性子集B下，A1和A2的混合邻域条件互信息熵定义为如下。
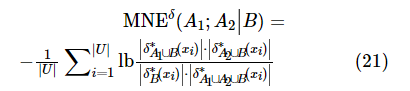
混合邻域条件互信息熵具有如下性质。
性质3：设混合型信息系统表示为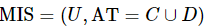
，属性子集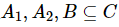
，那么可以得到式（22）。
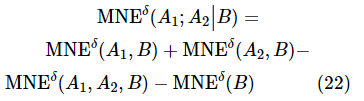
证明：根据定义6和定义7，可以得到式（23）。
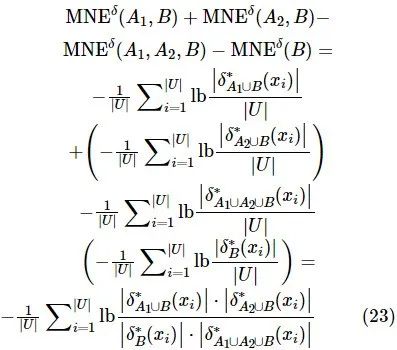
因此，满足
。
性质3表明，混合邻域条件互信息熵可通过混合邻域熵和混合邻域联合熵计算得到。性质4：设混合型信息系统表示为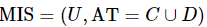
，属性子集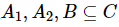
，那么可以得到式（24）。
证明：根据混合邻域条件互信息熵的定义可以直接得到。
根据性质3可以看出，当属性子集A1和A2相互独立时，混合邻域条件互信息熵的值为0。这表明混合邻域条件互信息熵可以展示给定条件下属性子集之间的依赖程度。将混合邻域条件互信息熵作为信息系统的属性子集评估函数，可以进行混合型信息系统的属性约简。
3 属性约简算法
本节将利用混合邻域条件互信息熵评估信息系统属性之间的依赖度和独立性，并构造出一种混合型信息系统的属性约简算法。
属性约简旨在寻找属性全集中与分类强相关的属性子集，因此属性约简集中的属性与信息系统的类属性具有强相关性。由于互信息熵展示了属性之间的相关性，因此将提出的混合型邻域互信息熵和混合型邻域条件互信息熵用于混合型信息系统属性之间的相关性度量。
定义11：设混合型信息系统表示为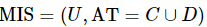
，属性子集
，关于决策属性集D的相关度
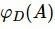定义如下。
其中 ，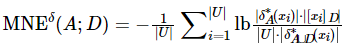
，[xi]D 为对象 xi在决策属性D下的等价类。
定义12：设混合型信息系统表示为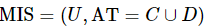
，属性子集
，属性子集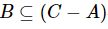
在属性子集A下关于决策属性D的相关度
定义如下。
其中，
。
利用混合型邻域互信息熵和混合型邻域条件互信息熵对混合型信息系统进行属性选择，可以进一步设计出一种属性约简算法。
利用混合型邻域互信息熵和混合型邻域条件互信息熵对混合型信息系统进行属性选择，可以进一步设计出一种属性约简算法。
算法1：基于邻域条件互信息熵的混合型信息系统属性约简算法
输入：混合型信息系统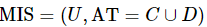
，邻域半径δ。
输出：属性约简结果red。
1.设置属性约简初始结果red=∅。
2.对于条件属性集C 中的每个属性∀a∈C，计算属性a与决策属性集D的相关度φD({a})。
3.找出2中相关度最大的属性amax，即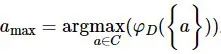
。
4.令
。
5.对于属性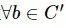
，计算属性b在属性约简集red 下关于决策属性 D 的相关
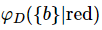度。
6.找出5中相关度最大的属性bmax，即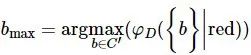
。
7.令
，并利用分类器对属性约简结果red进行分类精度计算，记录其分类精度结果。
8.重复5~7，直至
。
9.找出所有属性约简中分类精度最大的属性约简结果redbest。
10.返回属性约简集redbest。
在算法1中，主要计算量集中在属性集的邻域条件互信息熵上，而邻域条件互信息熵的计算主要是针对对象邻域类的计算，因此整个算法1的时间复杂度为
。
4 实验分析
为了验证本文提出的基于邻域条件互信息熵的属性约简算法的有效性，下面使用6个数据集进行实验分析，这些数据集见表1。这些数据集选择自UCI公共数据集，这些数据集均为混合型类型，适用于本文所提算法。
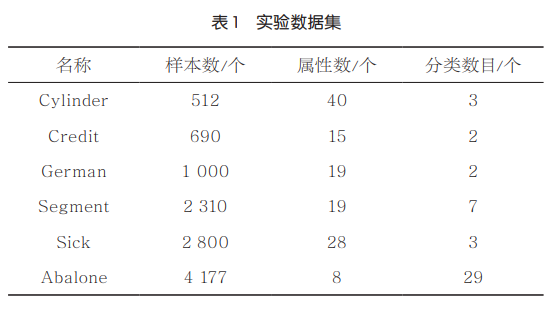
同时本文选择3种同类型的属性约简算法进行实验，分别为参考文献提出的属性约简算法（对比算法1），参考文献提出的属性约简算法（对比算法2）和参考文献提出的属性约简算法（对比算法3）。
所有算法的属性约简结果通过支持向量机（support vector machine，SVM）分类器和朴素贝叶斯（naive Bayesian， NB）分类器计算其分类精度，对每个数据集的约简结果进行20次十折交叉验证，并将平均值作为最终的分类精度结果。本实验在MATLAB 2018b上对所有属性约简算法进行实现，所有实验都在Intel(R) Core(TM)i3-7100上进行，CPU时钟速率为3.90 GHz，内存为8 GB。
在本文提出的属性约简算法中，不同的邻域半径取值对算法的属性约简结果将产生很大的影响。在参考文献中，学者们通过大量实验发现，当邻域半径过小时，其属性约简的长度较小，并且分类精度也较小；当邻域半径过大时，其分类精度不会更高。对于数据集归一化为0和1之间的值，当邻域半径为0.15左右时，其属性约简长度不是很大且分类精度最高，因此本实验选择邻域半径为0.15进行后续实验。
4.1 分类精度结果对比
分类性能是验证属性约简算法质量最有效和最直接的方法，其中，通常利用分类精度来衡量算法分类性能。表2和表3分别展示了本文属性约简算法与3种对比算法在SVM分类器和NB分类器下的平均分类精度结果，其结果使用“平均值±标准差”的形式表示。
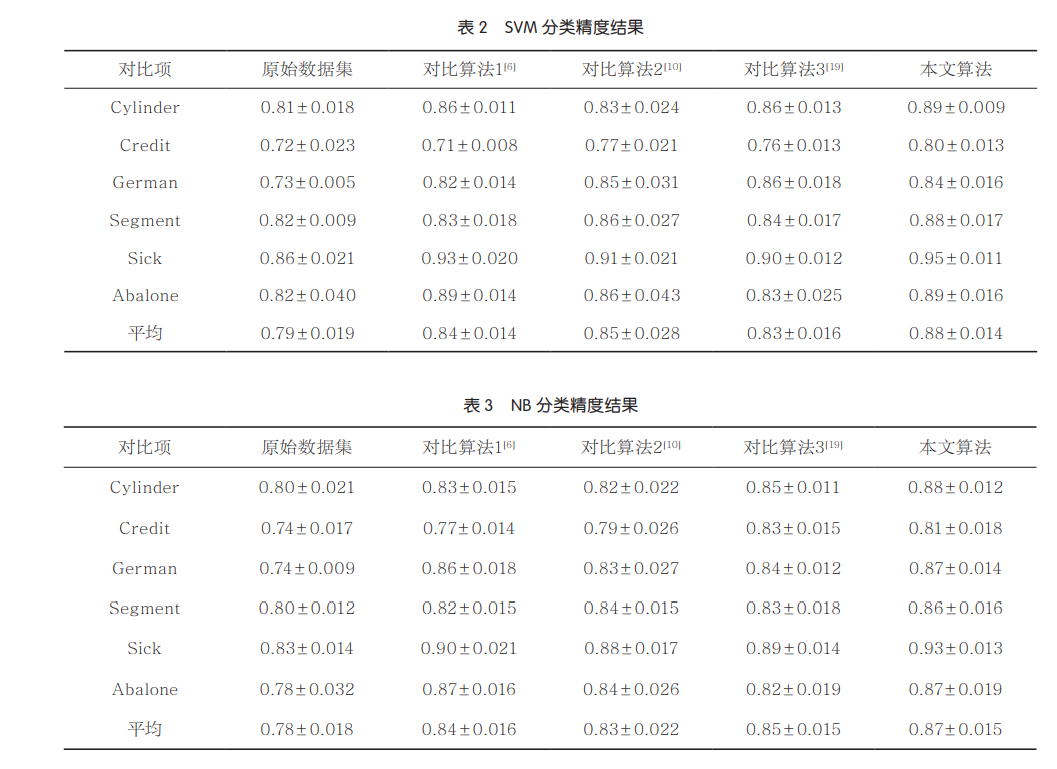
对比表2和表3的实验结果，可以得到如下结论。
● 与原始数据集的分类精度相比，3种对比算法和本文算法的SVM分类精度分别提高了6%、8%、5%和11%，NB分类精度分别提高了8%、6%、9%和12%。
● 在大部分数据集下，本文的属性约简算法具有更高的分类精度，例如对于利用SVM分类器计算得到的分类精度，本文算法在Cylinder、Credit和Segment等数据集上更高；对于利用NB分类器计算得到的分类精度，本文算法在German、Segment和Sick等数据集上更高。
● 同时本文算法在SVM分类器和NB分类器下的分类精度标准差大多小于或等于其余对比算法。从统计学的角度来看，本文算法的稳定性更高，这主要是由于本文算法通过邻域条件互信息熵选择属性，降低了最终约简结果中的冗余属性，从而提高了最终约简结果的分类性能。
4.2 属性约简长度对比
对于属性约简算法来说，属性约简结果的长度也是评估算法有效性的一项重要指标，表4展示了本文算法与3种对比算法的属性约简长度的对比结果。从表4可以看出，本文算法在各个数据集上的平均属性约简集长度为7.7，均低于其余3种算法，说明本文算法能够选择出规模更小的属性约简集。
4.3 属性约简效率对比
此外，算法的效率也是评估算法有效性和实用性的又一重要指标，图1给出了各个属性约简算法对每个数据集进行属性约简的用时。由图1可以看出，本文算法和对比算法1的用时均小于其余对比算法，这再一次证明了本文算法的有效性和优越性。
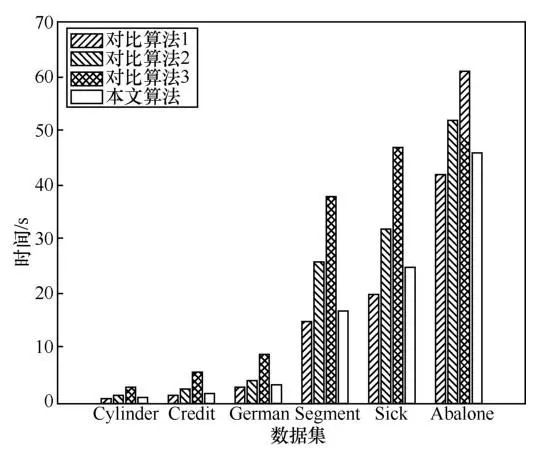
图1 不同算法运行时间
4.4 不同邻域半径分类精度结果对比
为了进一步对比本文算法和对比算法在不同邻域半径下属性约简的分类精度结果，下面将邻域半径区间[0.02,0.4]以0.02为间隔，分别取值对各个算法进行属性约简实验，并计算出每个邻域半径属性约简结果的分类精度。图2，图3，图4展示出了部分数据集在不同邻域半径下属性约简的分类精度结果。由图2~图4可以发现，在不同邻域半径下，本文算法的属性约简分类精度整体上高于其余3种对比算法，因此对于不同邻域半径，本文算法仍然具有更高的属性约简性能。
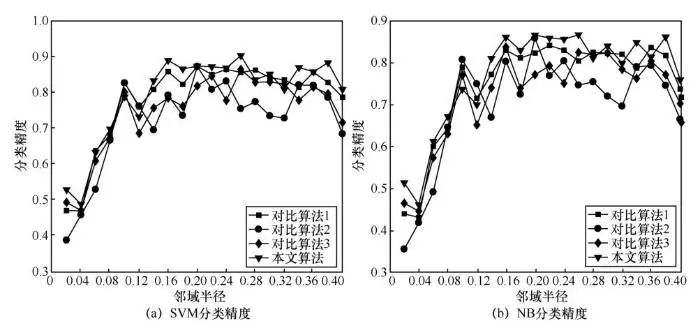
图2 Cylinder实验结果
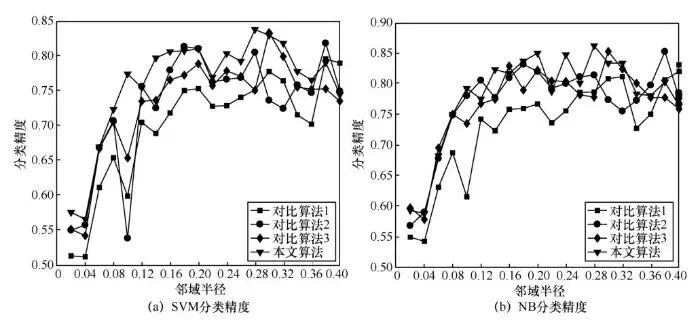
图3 Credit实验结果
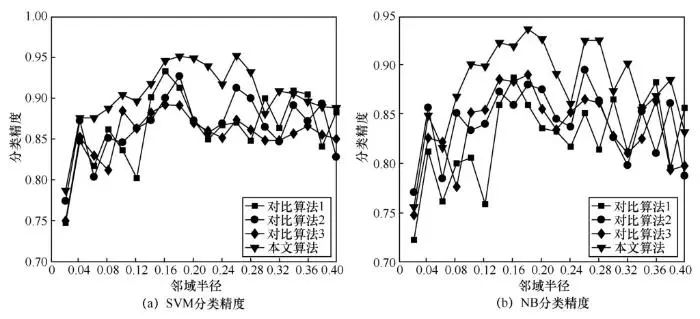
图4 Sick实验结果
综合各个环节的实验结果，与其他同类型属性约简算法相比，本文提出的属性约简算法具有更显著的有效性和优越性。
5 结束语
针对目前基于粗糙集理论的属性约简算法没有考虑属性之间的相关性和依赖性，本文提出一种基于邻域条件互信息熵的混合型信息系统属性约简算法。文中首先在传统邻域熵的基础上进一步提出了混合型邻域互信息熵模型和混合型邻域条件互信息熵模型，然后利用这两种熵模型进行混合型信息系统的属性相关性度量，最后设计出一种新的启发式属性约简算法，基于UCI数据集的属性约简实验表明，所提算法具有更高的属性约简性能。在将来的工作中，笔者将进一步研究邻域互信息熵模型和邻域条件互信息熵模型的增量式属性约简问题。
作者简介
兰海波（1979-），男，中国气象局公共气象服务中心高级工程师，主要研究方向为大数据处理技术、自然语言处理技术、数据库技术和气象服务信息系统的关键技术及应用。
联系我们:
Tel:010-81055448
010-81055490
010-81055534
E-mail:bdr@bjxintong.com.cn
http://www.infocomm-journal.com/bdr
http://www.j-bigdataresearch.com.cn/
转载、合作：010-81055307
大数据期刊
《大数据（Big Data Research，BDR）》双月刊是由中华人民共和国工业和信息化部主管，人民邮电出版社主办，中国计算机学会大数据专家委员会学术指导，北京信通传媒有限责任公司出版的期刊，已成功入选中国科技核心期刊、中国计算机学会会刊、中国计算机学会推荐中文科技期刊，以及信息通信领域高质量科技期刊分级目录、计算领域高质量科技期刊分级目录，并多次被评为国家哲学社会科学文献中心学术期刊数据库“综合性人文社会科学”学科最受欢迎期刊。
关注《大数据》期刊微信公众号，获取更多内容