概述
红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,它是在1972 年由Rudolf
Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J.Guibas
和Robert Sedgewick 修改为如今的"红黑树"。
红黑树在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)
时间内做查找,插入和删除,这里的n 是树中元素的数目。
它的统计性能要好于平衡二叉树。因此,红黑树在很多地方都有应用。在C++ STL中,很多部分(包括set, multiset, map, multimap)应用了红黑树的变体(SGI STL中的红黑树有一些变化,这些修改提供了更好的性能,以及对set操作的支持)。其他平衡树还有:AVL,SBT,伸展树,TREAP 等等。
二叉查找树(BST)具备的特性
1.左子树上所有结点的值均小于或等于它的根结点的值。
2.右子树上所有结点的值均大于或等于它的根结点的值。
3.左、右子树也分别为二叉排序树。
下图中这棵树,就是一颗典型的二叉查找树: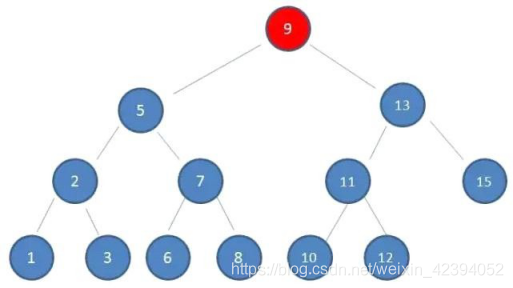
找10的过程:
1.查看根节点9:
2.由于10 > 9,因此查看右孩子13:
3.由于10 < 13,因此查看左孩子11: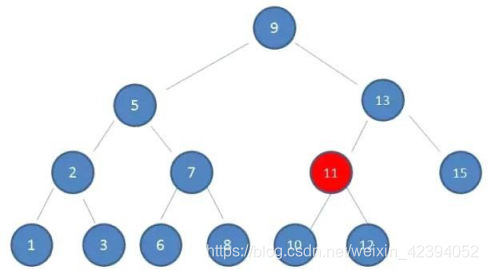
4.由于10 < 11,因此查看左孩子10,发现10正是要查找的节点: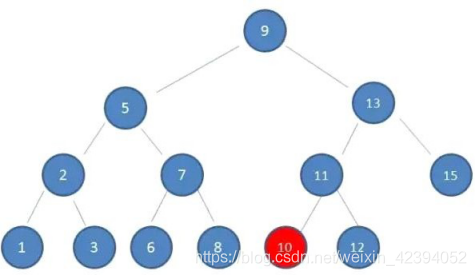
这种方式正式二分查找的思想,查找所需的最大次数等同于二叉查找树的高度
在插入节点的时候也是利用类似的方法,通过一层一层比较大小,找到新节点适合插入的位置。但二叉查找树仍然存在缺陷,体现在插入数据时。
假设初始的二叉查找树只有三个节点,根节点值为9,左孩子值为8,右孩子值为12: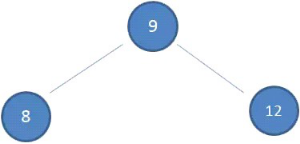
接下来我们依次插入如下五个节点:7,6,5,4,3。依照二叉查找树的特性,结果会变成什么样呢?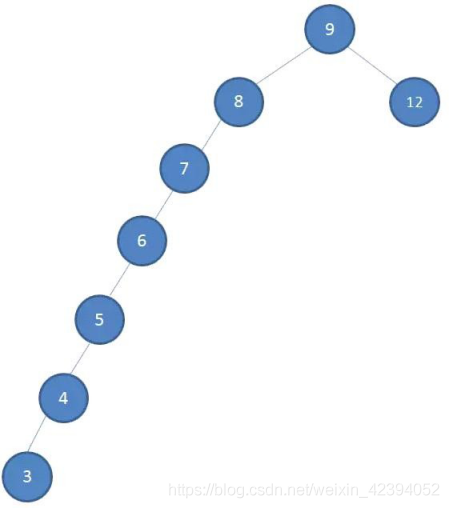
可以看到,二叉树变成了瘸子,查找几乎变成了线性查找。
红黑树
红黑树是一种自平衡的二叉查找树,除了符合二叉树的基本特性之外,它还具有附加特性:
1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点都是黑色的空节点(NIL节点)。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。下图中这棵树,就是一颗典型的红黑树:
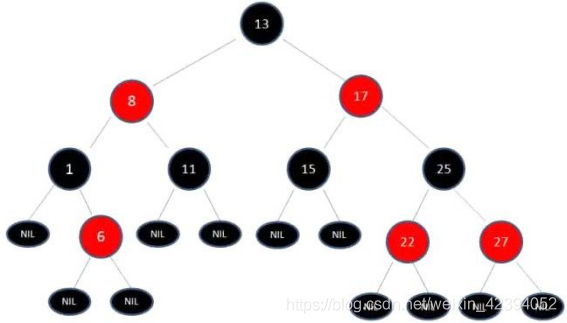
比如插入14数值后,会变成这样:
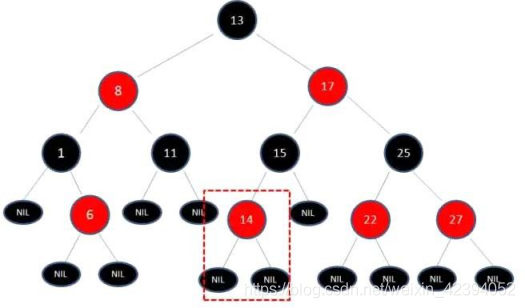
但很多情况下,向红黑树中插入数据会打破红黑树的5个特征,所以需要红黑树通过旋转来保证。比如插入21之后的树:
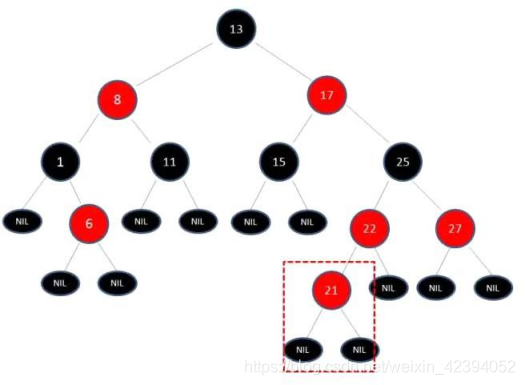
由于父节点22是红色节点,因此这种情况打破了红黑树的规则4(每个红色节点的两个子节点都是黑色),必须进行调整,使之重新符合红黑树的规则。
红黑树的变色与旋转
调整的方式是通过变色和旋转
变色是为了重新符合红黑树的规则,尝试把红色节点变为黑色,或者把黑色节点变为红色。
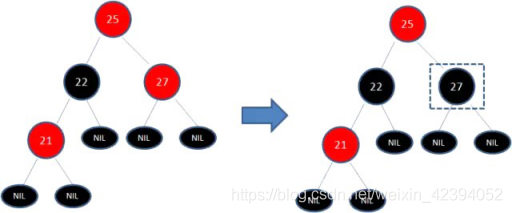
下图所表示的是红黑树的一部分,需要注意节点25并非根节点。因为节点21和节点22连续出现了红色,不符合规则4,所以把节点22从红色变成黑色:
但这样并不算完,因为凭空多出的黑色节点打破了规则5,所以发生连锁反应,需要继续把节点25从黑色变成红色: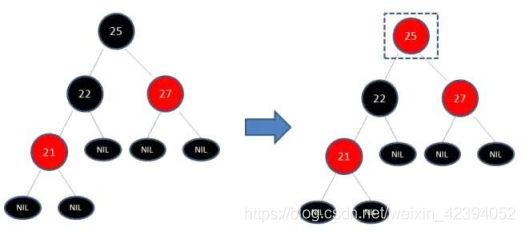
此时仍然没有结束,因为节点25和节点27又形成了两个连续的红色节点,需要继续把节点27从红色变成黑色: