【LeetCode】462. 最少移动次数使数组元素相等 II

题目大意

给你一个长度为n的整数数组 nums ，返回使所有数组元素相等需要的最少移动数。
在一步操作中，你可以使数组中的一个元素加1或者减1。

示例：

输入：nums = [1,2,3]
输出：2
解释：
只需要两步操作（每步操作指南使一个元素加 1 或减 1）：
[1,2,3]  =>  [2,2,3]  =>  [2,2,2]

输入：nums = [1,10,2,9]
输出：16

数据范围：

n == nums.length
1 <= nums.length <= 105
-109 <= nums[i] <= 109

思路

首先猜想最终相等的元素t的范围，最终应为数组中的某个元素。

• 若t小于数组中所有的元素，则此时增大t，那么所有元素变为t的次数将减小，可见t并非最优解；
• 若t大于数组中所有的元素，则此时减小t，那么所有元素变为t的次数将减小，可见t并非最优解；

可见t应该位于数组最大与最小值之间，下面证明最优的t可以取为数组中的某个元素，从而遍历数组元素即可。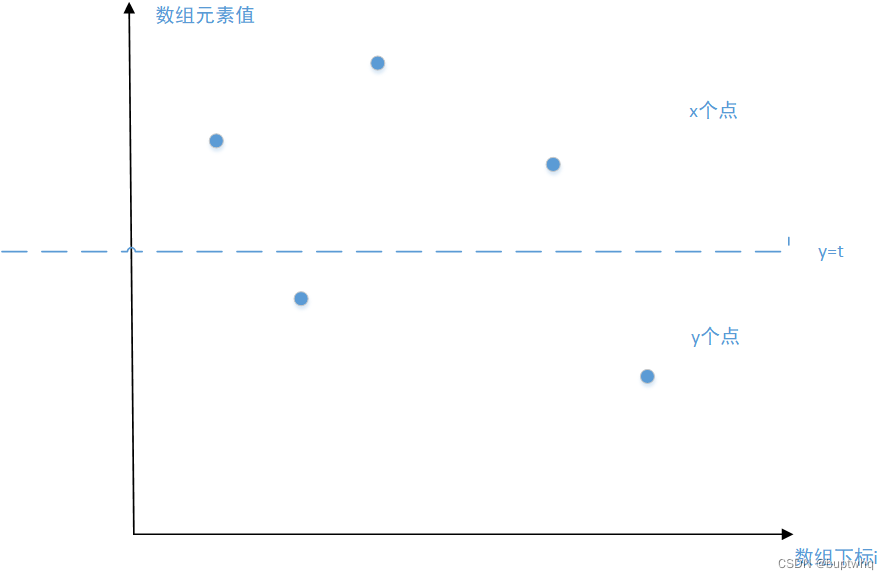

如上图所示，设t为数组最大与最小值之间的一个值，若t不为数组中的某个元素，则设此时大于t的元素有x个，小于t的元素为y个。
若x>y，则上移一格t，此时操作数变化量为-x+y<0，将会更优；
若x<y，则下移一格t，此时操作数变化量为x-y<0，将会更优；
若x=y，则无论上移与下移，操作数不变。
因此，可以看出若t不取数组中的某个元素值，则总可以通过调整t，使得操作数更少。因此t应该取数组中的某个值。
则问题转化为：
遍历数组中的数，找到某个元素t，使得t到其他元素值的距离之和最小。
由绝对值不等式可知，当t取数组中位数时，该距离之和最小。

代码

class Solution {
public:
    int minMoves2(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end()); // 首先排序，便于取中位数
        int res = 0;
        for(int i = 0; i < n; i ++ ){
            res += abs(nums[i] - nums[n / 2]);
        }

        return res;
    }
};

复杂度

时间复杂度：排序O(nlogn)，求和O(n)，因此总时间复杂度为O(nlogn)
空间复杂度：O(1)