统计学系列目录(文末有超级大礼):
统计学②——概率分布(几何,二项,泊松,正态分布)
统计学③——总体与样本
统计学④——置信区间
统计学⑤——假设验证
一、统计学是什么?
统计学分为两类,一类是描述性统计学,通过对数据的集中趋势和变异趋势的刻画来描述数据的分布情况,集中趋势有平均值,中位数和众数三个指标,变异趋势则有全距,四分位距,百分位距,方差,标准差等指标来衡量
另一类是推断统计学,通过对样本的统计来推断总体的参数和置信区间,以及对多变量进行相关性分析和回归预测。
用一句话就是:总结历史,预测未来
二、概率论基础
概率论是统计学中非常重要且基础的内容,因为统计学都是要基于数据分布,而数据分布就要依赖于概率分布。
1、概率是什么?
描述一个事件发生的可能性,范围在[0,1],值越接近于1,说明发生的可能性越大
引申:某一事件的信息熵就是基于其发生概率,概率越小信息熵越大,说明不确定性越大
2、各种事件?
独立事件:A,B如果为独立事件,则A发生不会影响B发生,B发生也不会影响A发生,比如连中了3次彩票为A,B为下一次仍中彩票,A,B就是独立事件,因为每次中彩票的概率都是一样的~
互斥事件:不可能同时发生的事件,比如A为吃饭噎住,B为吃饭不噎住,这两者不可能同时发生
3、何为交集并集?
A∩B: A和B的交集,P(A∩B)代表A和B同时发生的概率
若A,B为独立事件,P(A∩B) = P(A)*P(B)
若A,B为非独立事件,P(A∩B) = P(A)*P(A|B) = P(B)*P(A|B)
A∪B: A和B的并集,P(A∪B)代表A和B任意一个发生的概率
若A,B为独立事件,P(A∪B)=P(A) + P(B)
若A,B为非独立事件,P(A∪B)=P(A) + P(B) - P(A∩B)
3、条件概率是个啥?
指A发生时B发生的概率 = A,B同时发生的概率/A发生的概率
P(B|A) = P(A∩B)/P(A)
4、全概率公式是?
事件B有两种发生方式:与A一起发生,和不与A一起发生,即
P(B)= P(B|A)*P(A) + P(B|A’)*P(A’)
A’ 是指A不发生
5、贝叶斯定理好像有很名?
条件概率 + 全概率公式 → 贝叶斯定理
P(A∩B) = P(A)*P(B|A) = P(B)*P(A|B)
P(B)= P(B|A)*P(A) + P(B|A’)*P(A’)
贝叶斯定理:
P(A|B) = P(B|A)*P(A) / P(B|A)*P(A) + P(B|A’)*P(A’)
机器学习中有一类分类算法叫朴素贝叶斯,就是基于贝叶斯定理以及各特征之间相互独立而来
三、随机变量
随机变量是指一个可以等于一系列数值的变量,而这一系列中的每个值都有一个特定概率相关联
如果随机变量为X,X可能取值为(x1,x2,x3……)
P(X = x1)就是指X为x1的概率
1、随机变量期望如何算?
随机变量的期望是指在多次实验情况下,随机变量取值的均值是多少。
比如,女生喜欢早上起床量体重,早餐后量,午餐后量,晚上饿一顿量,健身后量…然后将量的结果除了次数就是期望,用E(X)表示
2、随机变量方差如何算?
为啥要计算一个随机变量的方差呢?有期望不就可以了吗?
方差是衡量变量与期望的差异,如果方差高,说明每一次的期望会变得越不可测,那么是不是越刺激呢?想想看老虎机,游戏抽卡,转盘等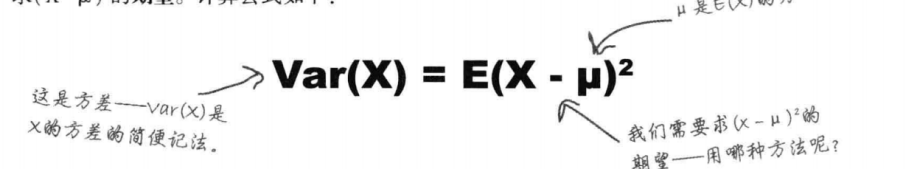

3、如果随机变量的取值做了线性变换,怎么计算?
假如X的取值均翻倍了,那么期望和方差会变化吗?
期望是翻倍,方差嘛,因为要平方,就变成了原来的4倍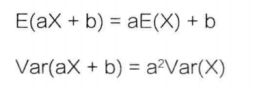
4、如果多个独立的随机变量一起,要如何计算呢?
比如刚才一个女生的体重变化,如果换做多个女生呢,如果计算整体期望和方差?
期望是直接相加,方差也是直接相加,这是因为每个变量的期望和方差都没变,只是累加到了一起
E(X + Y ) = E(X) + E(Y)
Var(X+ Y ) = Var(X) + Var( Y)
5、一个随机变量重复多次,怎么计算呢?
随机变量每次发生的期望和方差一样,因此多次也是直接汇总,与多个独立的随机变量同时发生一样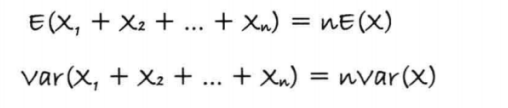
五、 业务实战
平台最近在做一个转盘游戏,概率老大交给我了。转盘上10个不同礼物,有4个价值非常高的礼物,其余都是小礼物。要求是既要保证礼物产出占消耗的95.5%,又要保证用户玩得爽,玩得上瘾不可自拔,然后大把大把充钱~~
这就是很典型的计算随机变量期望和方差的案例了,设用户收益为随机变量X,X取值就是10个礼物的价值,假设转盘一次的成本为10元,那么E(X) = 9.55元; 想要用户玩得爽,就得让方差尽可能大,每一次转盘的结果,要么惊喜过望,要么跌落谷底。这就变成了一个在期望确定情况下最大化方差的问题
E(X) = ∑ x*P(X=x) = 9.55
max Var(X) = E(X-μ)^2 = ∑(x-μ)^2*P(X=x)
我先假设只有3个礼物,分别计算了不同概率了期望在9.55时的方差(如下表),发现最大礼物和最小礼物的概率越大,中间礼物概率越小,方差越大,如果扩大到10个礼物,就是中间礼物概率尽可能小,在期望不大于9.55的前提下,尽可能提升大礼物概率,最后用1-其余礼物概率得到最小礼物概率,这样计算出来的方差最大。
从算法层面,确实这么做方差最大,可是从用户层面来说,要么抽到最小礼物,要么抽到最大礼物,且小礼物概率远远在于大礼物概率,中间礼物形同虚设,这种体验会很差,所以在实际业务中,还是会牺牲部分方差,给中间礼物设定一些概率,且随着礼物价值越大,概率越低,这样可以增加礼物抽到的多样性,比较不容易惹恼用户,但同时也尽量保证了较大的方差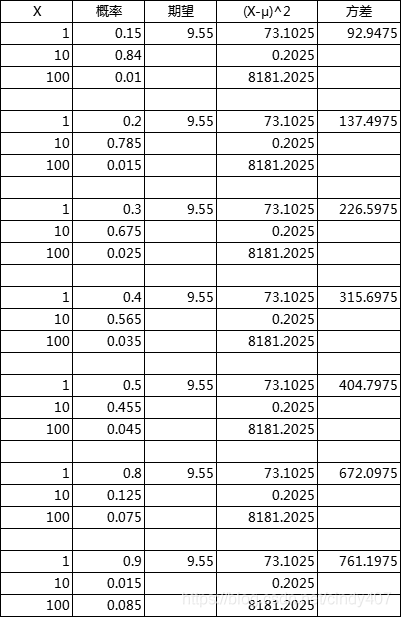
本人互联网数据分析师,目前已出Excel,SQL,Pandas,Matplotlib,Seaborn,机器学习,统计学,个性推荐,关联算法,工作总结系列。
微信搜索并关注 " 数据小斑马" 公众号,回复“统计”可以免费获取下方深入浅出统计学、统计学原理、赤裸裸的统计学等9本统计学入门到精通必备经典教材