Spark2.3 决策树 decision tree 源码解析
一、简介
决策树由节点和边构成,节点分为:内部节点和叶节点,其中内部节点表示一个特征,而叶节点表示一个分类,如下图
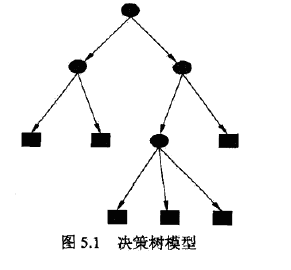
决策树,也可以看成是If Then规则,每个实例都会覆盖其中一条路径(或规则)。
二、树的构造
决策树的本质就是根据数据,归纳出一套分类规则,与数据矛盾最小的规则。从所有可能的决策树中,找到最优决策树是NP完全问题,因此通常采用启发式方法,近似求解。 通常就是递归的对特征进行分割,也就是对特征区间进行划分。
决策树生成算法
输入:训练数据集D,特征集合A
输出:决策树T
(1)如果D中所有实例都属于同一个类C_k,则T为单节点树,并将C_k作为该节点的类,返回T;
(2)如果A为空,则置T为单节点树,并将D中实例数最多的类C_k作为该节点的类,返回T;
(3)否则,从A中选择<strong>最优划分</strong>属性A_g,该属性有若干取值;
(4)根据最优属性A_g及其若干取值,<strong>将该节点分割成若干子节点</strong>:即将D分割构成若干子集D_i,返回由该节点及其子节点构成的树T;
(5)对子节点,以D_i为训练集合,A-A_g为特征集合(也可以A),递归调用(1)-(4)
上述算法只是决策树的大致生成流程,其中两个最重要的两个问题需要解决:1.最优划分属性的划分标准;2.如何分裂该属性构成若干子节点
1、如何分裂属性
分裂属性:根据属性的不同取值,将该属性分裂成若干子集,构成子节点。如何选择最优属性以及分裂值在下一节介绍,此处主要关注如何划分子集构成子节点。
(1)离散属性- 二叉树:假设a_i为该属性的一个子集,那么可以按照“属于该子集”和“不属于该子集”进行划分。例如该属性代表王者荣耀等级,那么a_i可以是集合“最强王者”,那么划分原则就是“王者”和“非王者”,两个子集
- 非二叉树:属性的每个取值为一个子集,进行划分。仍以上述王者荣耀为例,可以划分成如下子集:“青铜”集合,“白银”集合,“黄金”集合 等等,构造多个子节点。
根据最优分裂值split_point,划分为两个分支:值>split_point的分支 和 值<=split_point的分支。
2、最优划分属性和分裂值
选择最优属性的原则是使得节点包含的实例尽可能属于同一类,即使得节点不纯度(impurity)尽可能小。在saprk的ml中实现了三种impurity的度量方法:信息熵Entropy、基尼系数Gini、方差Variance。其中Entropy和Gini用来处理离散值,即处理分类问题,而Variance用来处理连续值,即回归。
2.1 Entropy 信息熵
信息熵是度量集合中样本不纯度的一种指标,假设当前集合为D,其中样本类别数为|y|,第k类样本所占的比例为p_k,那么集合D的信息熵Entropy则定义为:
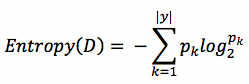
Entropy(D)代表不纯度,值越小,不纯度越低。在spark中的源码位于org.apache.spark.mllib.tree.impurity.Entropy
/** * :: DeveloperApi :: * information calculation for multiclass classification * @param counts Array[Double] with counts for each label * @param totalCount sum of counts for all labels * @return information value, or 0 if totalCount = 0 */ @Since("1.1.0") @DeveloperApi override def calculate(counts: Array[Double], totalCount: Double): Double = { if (totalCount == 0) { return 0 } val numClasses = counts.length var impurity = 0.0 var classIndex = 0 while (classIndex < numClasses) { val classCount = counts(classIndex) if (classCount != 0) { //freq 即为公式中的 p_k val freq = classCount / totalCount //impurity 即为 Entropy(D) impurity -= freq * log2(freq) } classIndex += 1 } impurity }
2.2 Gini 基尼系数
基尼系数也是衡量集合中样本不纯度的一种指标,假设当前集合为D,其中样本类别数为|y|,第k类样本所占的比例为p_k,那么集合D的基尼系数Gini则定义为:
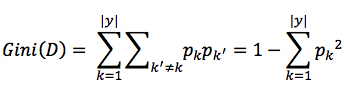
与Entropy类似,Gini(D)代表不纯度,值越小,不纯度越低。直观理解:任取两个样本不相同的概率,越小越纯。spark中的实现位于org.apache.spark.mllib.tree.impurity.Gini
/** * :: DeveloperApi :: * information calculation for multiclass classification * @param counts Array[Double] with counts for each label * @param totalCount sum of counts for all labels * @return information value, or 0 if totalCount = 0 */ @Since("1.1.0") @DeveloperApi override def calculate(counts: Array[Double], totalCount: Double): Double = { if (totalCount == 0) { return 0 } val numClasses = counts.length var impurity = 1.0 var classIndex = 0 while (classIndex < numClasses) { //freq为上述公式中的p_k val freq = counts(classIndex) / totalCount //gini=1-Sum(freq * freq) impurity -= freq * freq classIndex += 1 } impurity }
2.3 Variance 方差
Variance方差也是衡量集合中样本不纯度的一种指标,因为只是针对连续值,因此只能用于处理回归决策树。假设当前集合为D,样本数量为N,每个样本的值为y_i,那么集合D的Variance方差则定义为:最后转化为平方和以及和的平方

回归决策树中,将节点中包含的所有样本y_i的平均值作为该节点的预测值。该公式直接表示集合D的方差,因此代表该节点预测值与真实值(所有样本)的差距,也就是不纯度impurity。 spark中的实现位于org.apache.spark.mllib.tree.impurity.Variance
* :: DeveloperApi :: * variance calculation * @param count number of instances * @param sum sum of labels * @param sumSquares summation of squares of the labels * @return information value, or 0 if count = 0 */ @Since("1.0.0") @DeveloperApi override def calculate(count: Double, sum: Double, sumSquares: Double): Double = { if (count == 0) { return 0 } val squaredLoss = sumSquares - (sum * sum) / count squaredLoss / count }
2.4 信息增益
在决策树中,信息增益(informatioin gain, IG)指根据某个特征进行分裂时,不确定性减少的程度,即不纯度下降的程度。对于二叉决策树,该节点根据某个特征进行分裂成左右两个子节点,那么怎么衡量分裂的好坏呢,怎么找到最好的分裂特征呢?根据IG原理:选择使信息增益最大的特征f进行分裂,即使不纯度下降的最多的特征。
上述 2.1-2.3 都是描述数据的不纯度指标,用impurity表示,都可以用来计算信息增益,在spark中也是这么做的:
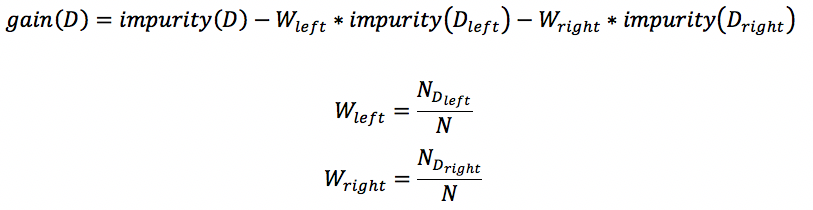
根据上述公式,遍历每个特征f及其每个分割值,找到使得gain最大的特征和相应分裂值,即为最优分裂特征和最优分裂值。
注:
此处只对决策树进行了理论介绍,许多实现细节还未介绍:例如关于如何根据特征划分成不同的子节点,连续值和离散值处理的不同点等。spark中决策树的具体实现细节和trick在随机森林randomforest中,决策树作为随机森林的一个特例(树数量=1),因此具体代码和详细内容将在下一篇random forest中进行介绍