数据分析方法——方差分析

3.1 单因素方差分析

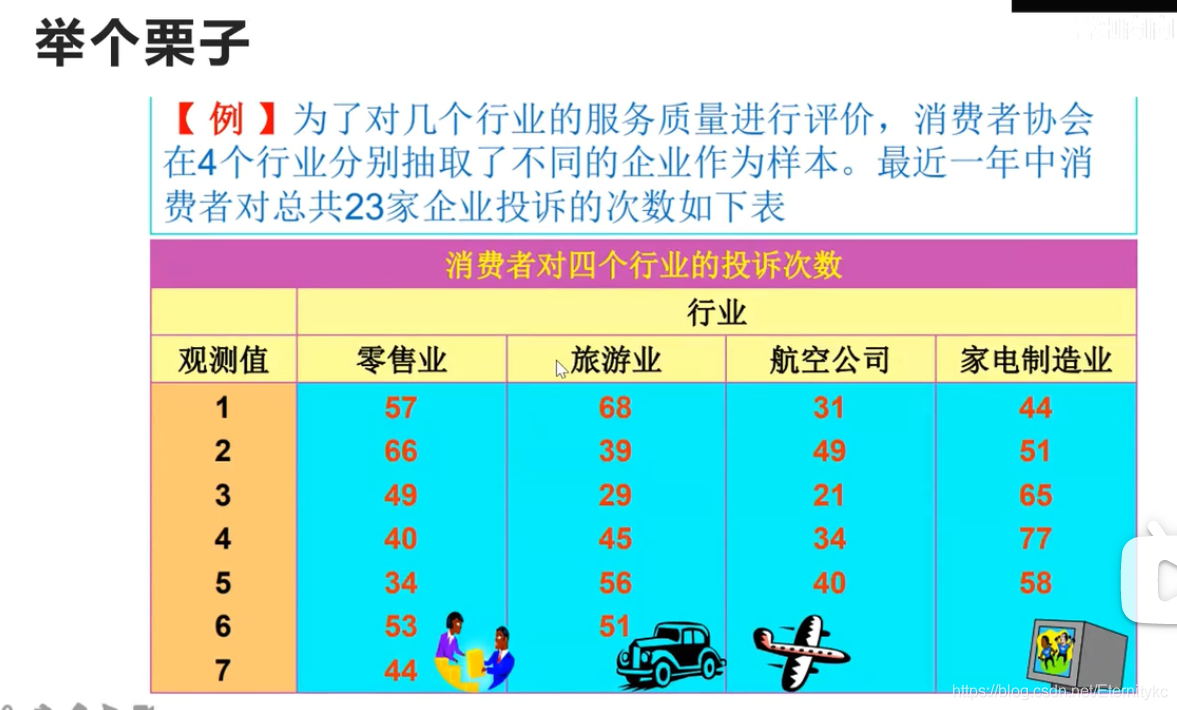
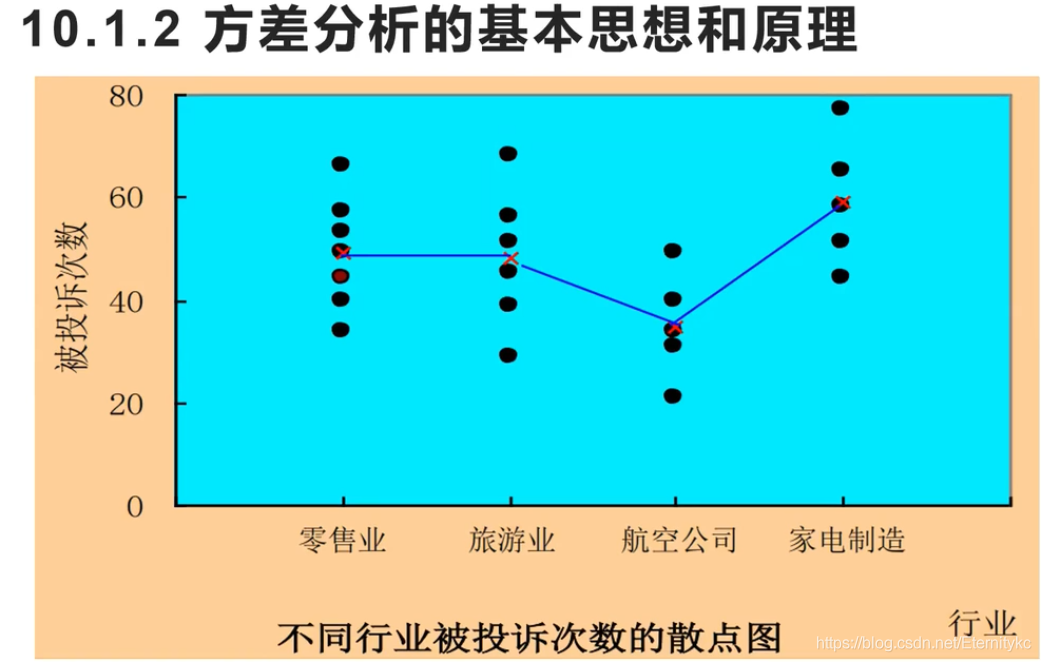
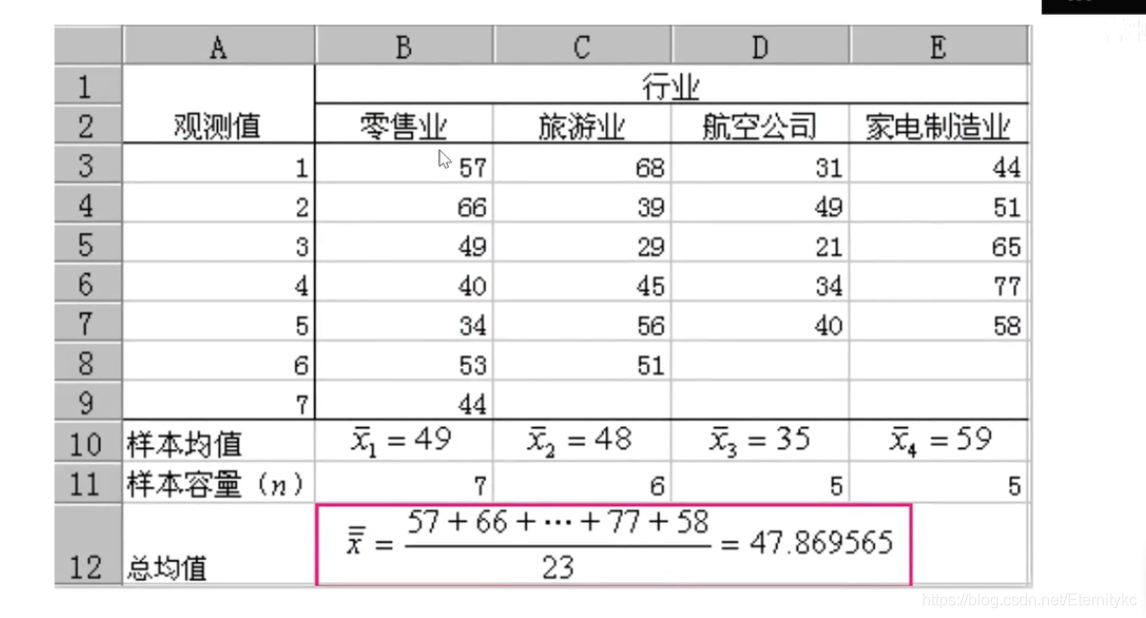
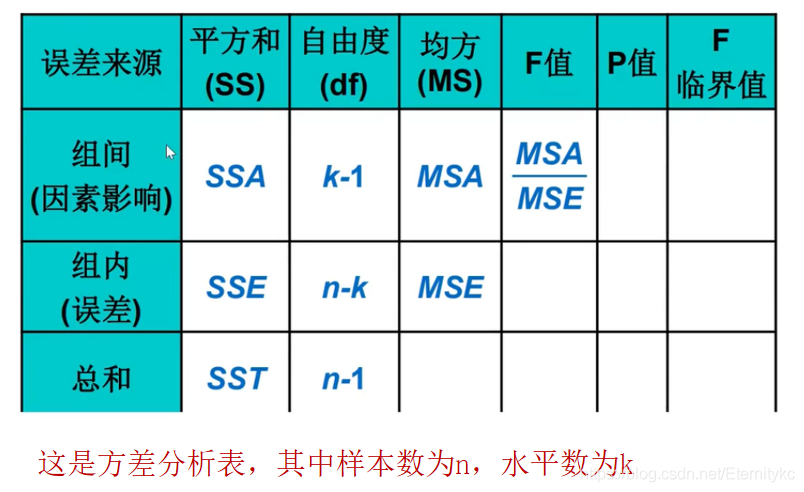
1.在该例子中，组间SSA=1456，组内SSE=2708
2.MSA的自由度为 k-1 = 3 --> MSA=1456/3 = 485
3.MSE的自由度为 n-k = 23-4 =19 -->MSE=2709/19 = 142

示例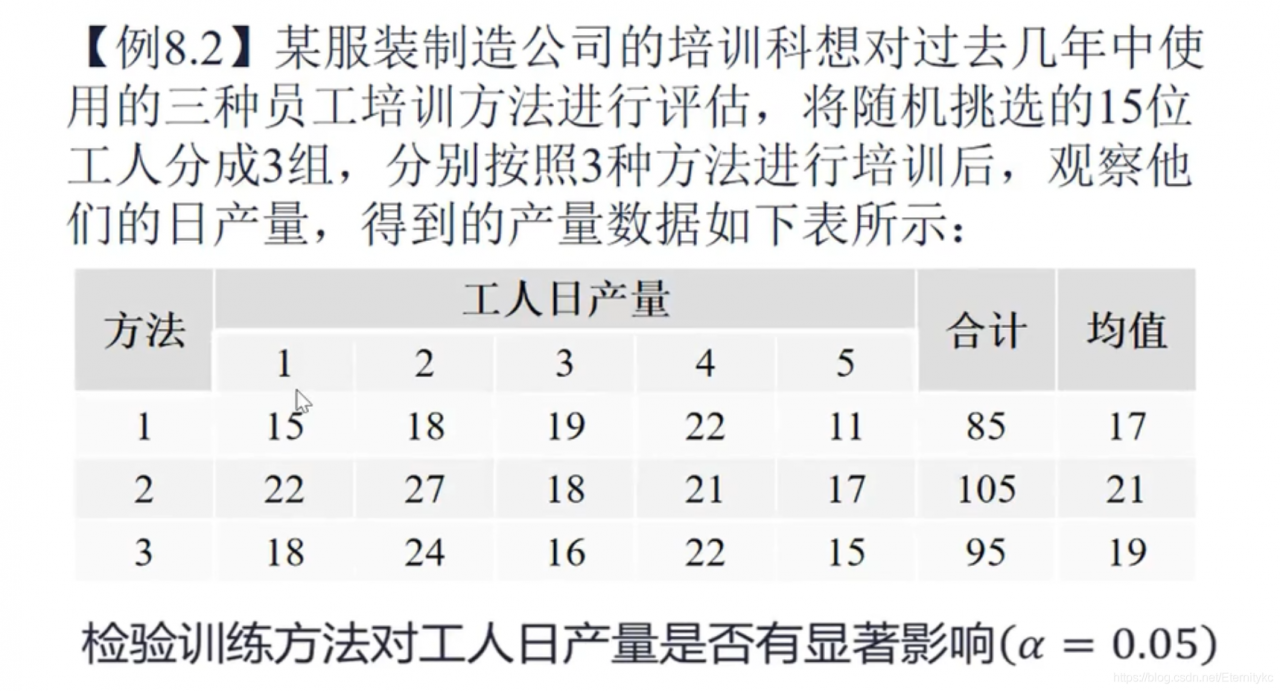

总均值=19  
SST=232  								df=n-1=14
SSA=5*(17-19)^2 + 5*(21-19)^2 = 40		df=k-1=2
SSE=192									df=n-k=15-3=12
MSA = SSA/(k-1) = 20
MSE = SSE/(n-k) = 192/12 = 16
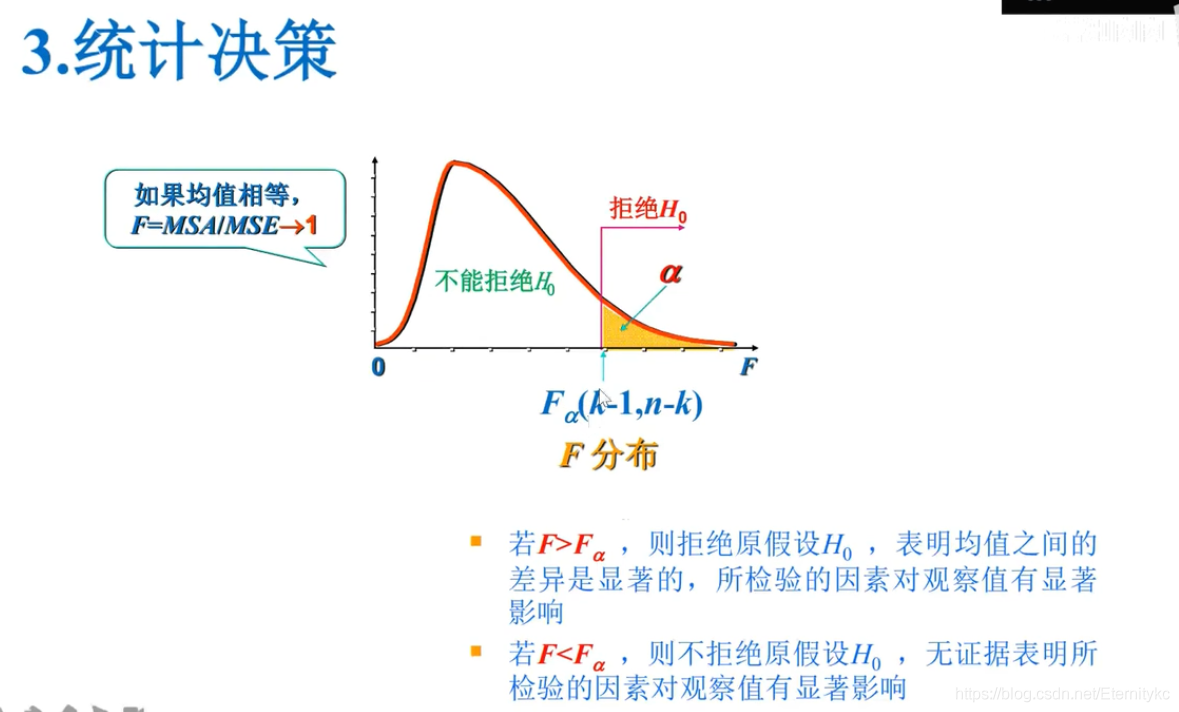
F = MSA/MSE = 1.22 【这个是算错了还是？？？】
该F需要和 F(k-1,n-k) = F(2,12) = 3.89
F=1.22<3.89  --> 不拒绝原假设，即三种训练方法对产量没有显著影响

3.1.5 gray

方差分析在判断出存在显著性差异后不知道是哪几个水平存在
故后续需要啊采用LSD方法来判断两个总体的均值是否相等

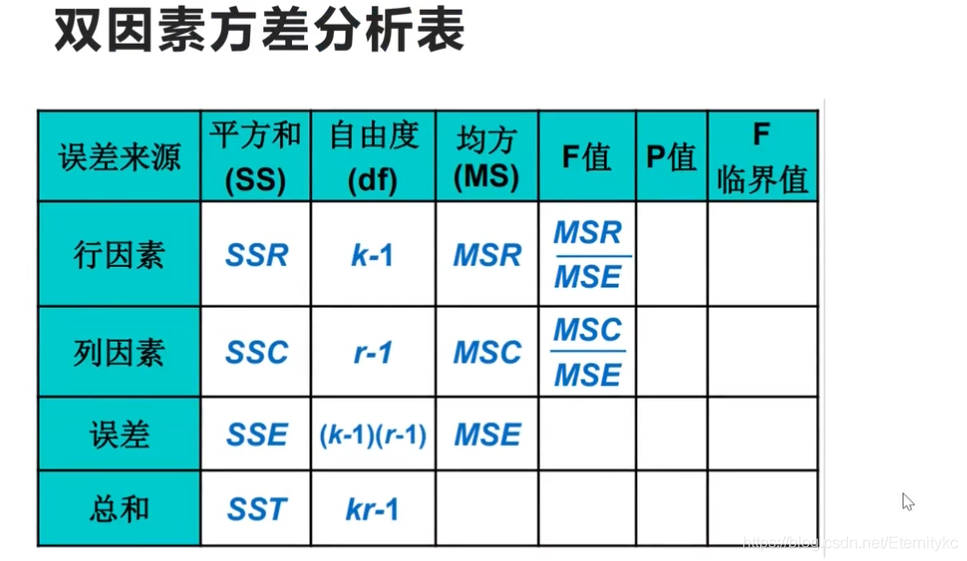
3.2 双因素方差分析

这里与单因素的假定是一样的。

1.无交互作用的双因素方差分析

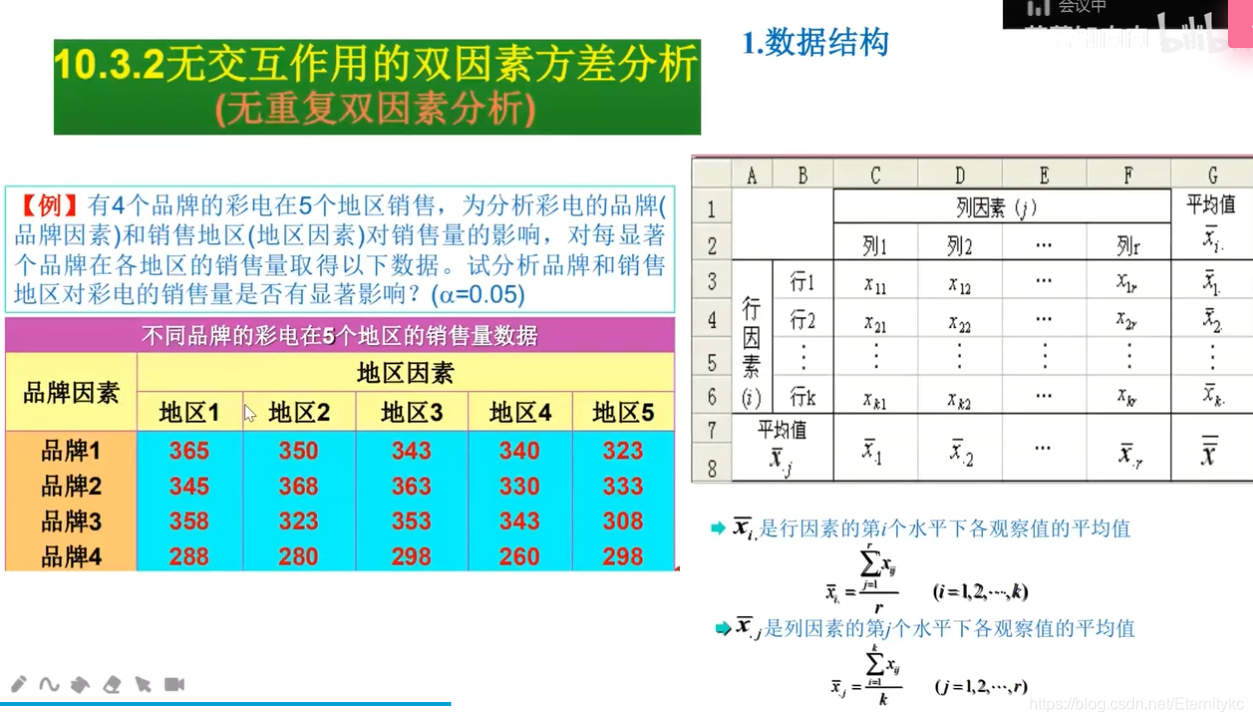
其中，该图的矩阵为Ak*r，即k行r列，有k个行因素，有r个列因素

分别计算行均值和列均值，计算总均值(同样是所有相加/n)
行均值是xi.的符号，而列均值是x.j的符号

总误差平方和，行因素误差平方和SSR，列因素误差平方和SSC（这俩也就是原来的组间平方和）
上面几个的计算没有什么特别的，和单因素一样的方法
以及误差项平方和SSE，这个有点特别了，x+总均值-行均值-列均值
等式：SST=SSR+SSC+SSE.

自由度 (k行r列，即k个行因素，r个列因素)
1.SST -> kr-1
2.SSR -> k-1
3.SSC -> r-1
4.SSE -> (k-1)*(r-1) 

so->

行因素均方MSR：SSR/(k-1)
列因素均方MSC：SSC/(r-1)
误差项均方MSE：SSE/[(k-1)*(r-1)]

so->

行检验统计量FR = MSR/MSE ~ F(k-1,(k-1)(r-1))
列检验统计量FC = MSC/MSE ~ F(r-1,(k-1)(r-1))
<注意:F的第一个元素为SSR(SSC)的自由度
第二个元素为MSE的自由度，这样就好记拉！>

so->

同样的，如果F>临界值，拒绝原假设，即有显著关系

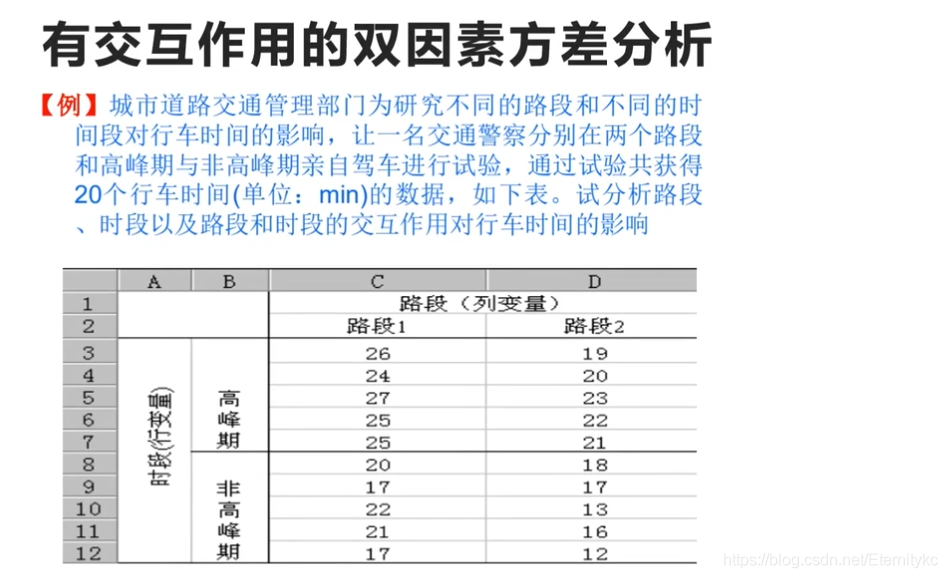
2.有交互作用的双因素方差分析

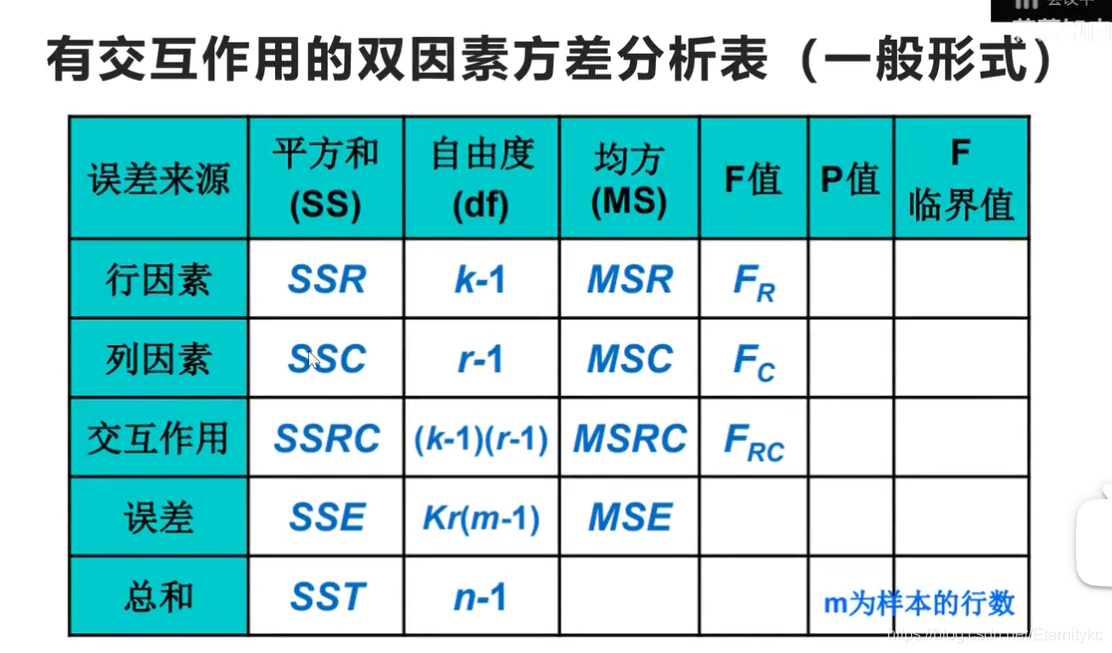
这个双因素方差分析表与原来相比多列1个交互作用，SSRC，自由度(k-1)(r-1)
同时，误差项的自由度变成了kr(m-1)，m为样本的行数