梯度消失与梯度爆炸

原文链接：https://www.yuque.com/yahei/hey-yahei/gradient_vanish_explode

在深度学习任务中，随着层数的增加，因为反向传播的链式求导规则，梯度容易出现指数形式地减小或增长，从而导致梯度消失（非常小，训练缓慢）或梯度爆炸（非常大，训练不稳定）现象的发生。
相比CNN，RNN更容易出现梯度消失和梯度爆炸问题，这一点在《梯度消失与梯度爆炸 - 为什么RNN通常不用ReLU？ | Hey~YaHei!》中有一些简单的讨论。

参考：

1. 《Hands-On Machine Learning with Scikit-Learn and TensorFlow(2017)》Chap11
2. 《卷积神经网络——深度学习实践手册(2017.05)》
3. 《详解深度学习中的梯度消失、爆炸原因及其解决方法 | 知乎, DoubleV》

解决梯度消失和爆炸的常用技术（本文只讨论前五项）：

1. 【减少爆炸】合理的随机初始化策略（Xavier Initialization、He Initialization等）
2. 【减少消失】使用非饱和函数作为激活函数（如ReLU）
3. 【减少消失和爆炸】批量归一化（Batch Normalization, BN）
4. 【减少爆炸】梯度裁剪（Gradient Clipping）
5. 【减少消失和爆炸】复用预训练层
6. 【较少爆炸】权重正则化（Weights Regularization）
7. 【减少消失】残差结构
8. 【减少消失】LSTM

随机初始化

参考：《深度学习500问 - Ch03深度学习基础 - 3.8权重偏差初始化》
模型的训练需要对参数进行初始化，然后用反向传播算法和梯度下降法更新参数，如何初始化参数是有讲究的。通常会随机初始化为一些相对比较小的数值，防止参数过大导致梯度爆炸；但也不能太小，否则梯度太小，收敛就太慢。
考虑一些简单的初始化方式，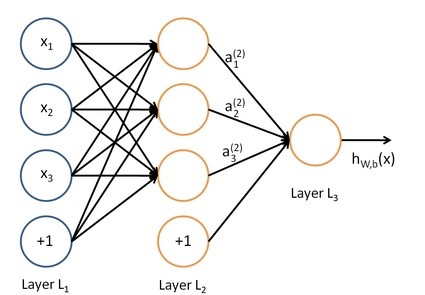

前向传播：
$$\begin{gathered} a_1^{(2)}=f(W_{11}^{(1)}{x}_1+W_{12}^{(1)}{x}_2+W_{13}^{(1)}{x}_3+b_1^{(1)}) \\ {a}_2^{(2)}=f(W_{21}^{(1)}{x}_1+W_{22}^{(1)}{x}_2+W_{23}^{(1)}{x}_3+b_2^{(1)}) \\ {a}_3^{(2)}=f(W_{31}^{(1)}{x}_1+W_{32}^{(1)}{x}_2+W_{33}^{(1)}{x}_3+b_3^{(1)}) \\ {h}_{W,b}(x)=a_1^{(3)}=f(W_{11}^{(2)}{a}_1^{(2)}+W_{12}^{(2)}{a}_2^{(2)}+W_{13}^{(2)}{a}_3^{(2)}+b_1^{(2)}) \end{gathered}$$

反向传播：
$$\begin{array}{rl}\frac{\partial J(W,b;x,y)}{\partial W_{ij}^{(l)}}& =a_j^{(l)}{\delta }_i^{(l+1)}\\ \frac{\partial J(W,b;x,y)}{\partial b_i^{(l)}}& ={\delta }_i^{(l+1)}\end{array}$$
其中，$${\delta }^{(l)}$$是第$$l$$层的输出误差，
$${\delta }_i^{(l)}=(\sum _{j=1}^{s_{t+1}}{W}_{ji}^{(l)}{\delta }_j^{(l+1)})f^{\prime }(z_i^{(l)})$$
$$a_i^{(l)}=f(z_i^{(l)})$$，如果使用的是sigmoid激活函数
$$f^{\prime }(z_i^{(l)})=a_i^{(l)}(1-a_i^{(l)})$$

1. 权重均初始化为零：梯度均为0，是无法进行训练的

   $$W_{ji}^{(l)}=0\Rightarrow {\delta }_i^{(l)}=(\sum _{j=1}^{s_{t+1}}{W}_{ji}^{(l)}{\delta }_j^{(l+1)})f^{\prime }(z_i^{(l)})=0\Rightarrow \{\begin{array}{l}\frac{\partial J(W,b;x,y)}{\partial W_{ij}^{(l)}}=a_j^{(l)}{\delta }_i^{(l+1)}=0\\ \frac{\partial J(W,b;x,y)}{\partial b_i^{(l)}}={\delta }_i^{(l+1)}=0\end{array}$$

2. 参数均初始化为同一个值：初始值相同，梯度也相同，最终训练后所有参数也相同，训练是无效的

$$\{\begin{array}{ll}{W}_{ji}^{(l)}& 相等\\ b_i^{(l)}& 相等\end{array}\Rightarrow a_j^{(l)}相等\Rightarrow {\delta }_i^{(l)}=(\sum _{j=1}^{s_{t+1}}{W}_{ji}^{(l)}{\delta }_j^{(l+1)})f^{\prime }(z_i^{(l)})相等\Rightarrow \{\begin{array}{l}\frac{\partial J(W,b;x,y)}{\partial W_{ij}^{(l)}}=a_j^{(l)}{\delta }_i^{(l+1)}相等\\ \frac{\partial J(W,b;x,y)}{\partial b_i^{(l)}}={\delta }_i^{(l+1)}相等\end{array}$$

直观上讲，卷积层包含许多滤波器，它们用来提取输入特征图上的特征。通过随机初始化，让每个滤波器最初都随机关注不同的特征，有助于训练出倾向于提取不同特征的滤波器，避免冗余滤波器的出现。而随机初始化，多数采用的是均匀分布或是高斯分布的初始化，各个初始化方式不同之处在于均匀分布的范围、高斯分布的标准差的确定方式不同，事实上，随着BN层的普遍使用，随机初始化的形式已经变得不再那么重要。

Xavier Initialization(Glorot Initialization)

论文：《Understanding the difficulty of training deep feedforward neural networks(2010)》
作者Xavier建议：使每一层的输入输出的方差相等，而且正反向传播的梯度也相等

并针对sigmoid激活函数（logistic激活函数）提出一种初始化方式：

1. 各权重用均值为0的正态分布随机数进行初始化，并且标准差根据输入、输出的维度确定——

   $$\sigma =\sqrt{\frac{2}{n_{inputs}+n_{outputs}}}$$
   参考：torch.nn.init.xavier_normal_

2. 用[-r, r]的均匀分布随机数进行初始化——

   $$r=\sqrt{\frac{6}{n_{inputs}+n_{outputs}}}$$
   参考：torch.nn.init.xavier_uniform_
   （在卷积层中，$$n_{inputs}$$和$$n_{outputs}$$指的是输入、输出特征图的通道数量）

He Initialization(Kaiming Initialization)

论文：《Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification(2015)》

• tanh激活函数

$$\sigma =4\sqrt{\frac{2}{n_{inputs}+n_{outputs}}}$$
$$r=4\sqrt{\frac{6}{n_{inputs}+n_{outputs}}}$$

• relu激活函数及其变体

  $$\sigma =\sqrt{2}\sqrt{\frac{2}{n_{inputs}+n_{outputs}}}$$

  $$r=\sqrt{2}\sqrt{\frac{6}{n_{inputs}+n_{outputs}}}$$
  （在卷积层中，$$n_{inputs}$$和$$n_{outputs}$$指的是输入、输出特征图的通道数量）

数据敏感的参数初始化

是一种根据自身任务数据集量身定制的参数初始化方式；
论文：《Data-dependent Initializations of Convolutional Neural Networks(2016)》
代码：philkr/magic_init | github

激活函数

卷积、全连接、BN都是典型的线性操作，而真实世界的模型往往是高度非线性的，激活函数通常采用的都是非线性函数，主要目的就是为了给深度学习模型引入非线性特征，从而更好的模拟、拟合出非线性的真实情况。采用非饱和的激活函数，可以防止梯度在层层反传的过程中逐渐减小，导致梯度消失。

激活函数通常会跟全连接层、卷积层紧密配合使用，但也不总是如此，比如MobileNetv2、ShuffleNet等就取消一些非线性激活来避免信息损失，相关论述可以参考《MobileNet全家桶 - 通道收缩时使用非线性激活带来信息丢失 | Hey~YaHei!》。

各类激活函数基本都可以在 torch.nn#non-linear-activations-weighted-sum-nonlinearity 中找到。

sigmoid

tanh

参考：《在神经网络中，激活函数sigmoid和tanh除了阈值取值外有什么不同吗？| 知乎》
除了sigmoid，tanh函数也经常用作激活函数，它们之间是线性相关的：

$$\tanh (x)=\frac{\sinh (x)}{\cosh (x)}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$$

$$1-2\mathrm{sigmoid}(x)=-\tanh \left(\frac{x}{2}\right)$$

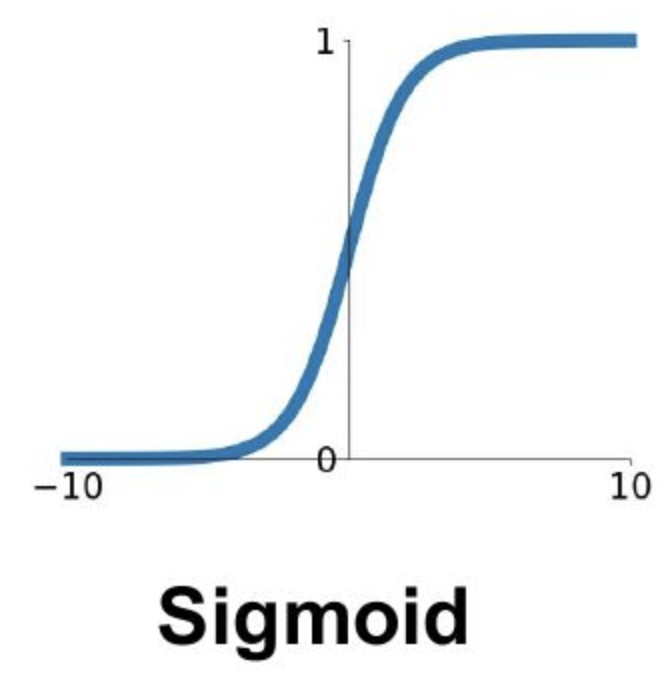
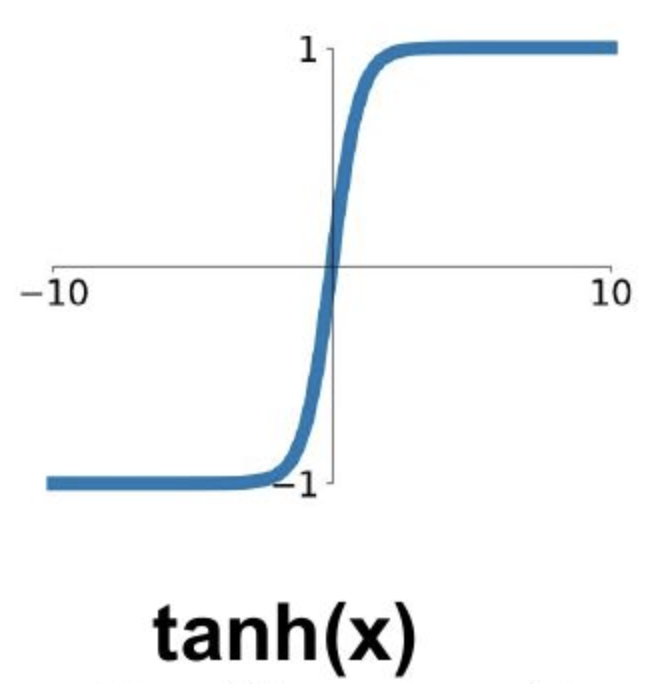
一般来说，tanh收敛速度要快于sigmoid，

1. sigmoid的值域为$$(0,1)$$，均为正数
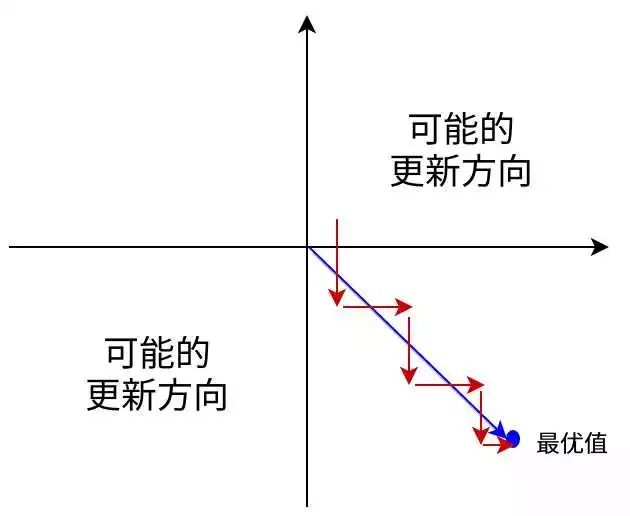
   考虑《梯度消失与梯度下降 - 随机初始化 | Hey~YaHei!》推导出的反向传播公式$$\frac{\partial J(W,b;x,y)}{\partial W_{ij}^{(l)}}=a_j^{(l)}{\delta }_i^{(l+1)}$$会发现，由于$${\delta }_i^{(l+1)}$$相同，且$$a_j^{(l)}>0$$，$$\frac{\partial J(W,b;x,y)}{\partial W_{ij}^{(l)}}$$符号必定相同。那么每次迭代，这一组权重的更新方向会比较单一，不利于训练。
   （简单地考虑只有两个参数的情形，参数的更新方向只能是第一或第三象限，优化路径会变得比较曲折，课程cs231中将其称之为zig zag）

而tanh的值域为$$(-1,1)$$，既有正数又有负数，就不会出现类似的问题

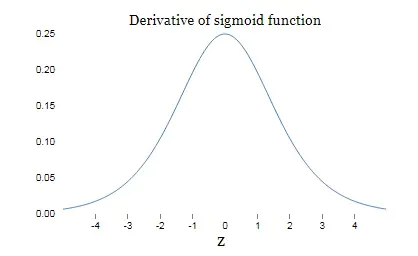
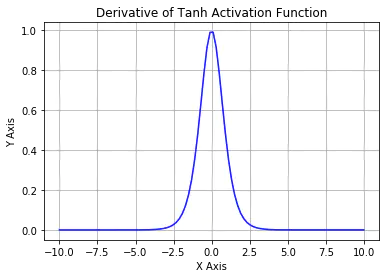
2. sigmoid的导数值域为$$(0,0.25]$$，而tanh的导数值域为$$(0,1.0]$$，更新速度会快一些

ReLU

参考：

• 《【机器学习】saturate的解释 | CSDN》
• 《深度学习——激活函数Sigmoid/Tanh/ReLU | CSDN》

线性整流函数（Rectified Linear Unit, ReLU），也称修正线性单元，可以看作是softplus的一个hard版本：
$$SoftPlus(z)=log(1+e^z)$$
$$ReLU(z)=max(0,z)$$

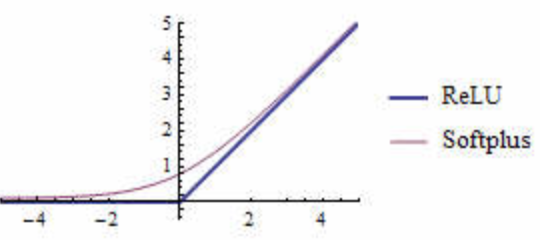
• 优势
  • sigmoid和tanh是饱和（saturate）函数

sigmoid的输出限定在[0, 1]之间；tanh的输出限定在[-1, 1]之间；

而relu的输出为[0, +∞)，为非饱和函数

• 计算非常简单、快速
• 导数简单，要么阻断（0）要么直通（1），不像sigmoid和tanh存在衰减，收敛速度快
  
• 存在问题（dying relus）

当输入的加权和为负数时，relu有可能陷入死区而每次激活都只输出0（因为当输入为负数时relu的梯度一直是0），最终导致网络崩溃；

• 变体（解决dead问题）

论文 《Empirical Evaluation of Rectified Activations in Convolution Network(2015) 》比较了各种不同变体的表现

• leaky relu

$$LeakyReL{U}_{\alpha }(z)=max(\alpha z,z)$$

其中 $$\alpha$$ 使 $$z<0$$ 时有一个小梯度，使得relu不会彻底“死亡”，在接下来的训练中有可能被“复活”；

通常 $$\alpha$$ 取0.01

• randomized leaky relu（RReLU）

leaky relu的变体，其中 $$\alpha$$ 在训练中是一个随机数，最终测试时固定为一个平均值

• parametric leaky relu（PReLU）

leaky relu的变体，其中 $$\alpha$$ 作为模型的一个参数参与训练

论文指出，PReLU在大型图片数据集上有很好的表现，但在小数据集上很快就过拟合

• exponential linear unit（ELU）

论文《FAST AND ACCURATE DEEP NETWORK LEARNING BY EXPONENTIAL LINEAR UNITS (ELUS)(2016)》指出，ELU可以减少训练时间，并且在测试集上有更好的表现

KaTeX parse error: No such environment: equation at position 7: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ ELU_\a…
- ELU在 $$z<0$$ 时有负数输出，使得单元的平均输出更接近于0，这有助于缓解梯度消失的问题
- $$\alpha$$ 通常取1，但也可以采用其他方式来确定它的值
- 当 $$z<0$$ 时有非0梯度，有助于避免dying relu问题
- 函数光滑，有助于加速梯度下降（而且当 $$\alpha =1$$ 时，函数在 $$z=0$$ 上可导）
- ELU因为多了指数运算，其计算要比relu慢，但是因为能更快收敛，所以在训练有一定的补偿；不过在测试时，还是会比较慢

• 选择
  • 一般来说：ELU > leaky ReLU（及其变体） > ReLU > tanh > logistic
  • 优先使用~~ELU，但如果需要考虑预测的开销，那么可以使用leaky ReLU~~及其变体
  • 如果还要进一步节省时间和计算力，可以使用交叉验证来评估不同的激活函数
  • 如果网络出现过拟合而不想花时间去调参和测试，可以使用~~RReLU~~
  • 如果你拥有非常大的数据集，那也可以直接使用~~PReLU~~
  • 多数情况下不容易出现dead问题，当然用这些变种可能带来细微的提升，但其收益往往不及所要付出的计算代价，主流上还是原始的ReLU或者简单的变体如ReLU6用的多一些

为什么RNN通常不用ReLU？

参考：《RNN 中为什么要采用 tanh，而不是 ReLU 作为激活函数？ - 何之源的回答 | 知乎》
在CNN上，ReLU几乎已经取代掉sigmoid和tanh，可在RNN中饱和的sigmoid和tanh依旧随处可见——

1. 在RNN中，不饱和激活容易带来数值快速膨胀

用数学符号表示RNN，
$$\begin{array}{rl}{a}_i& =W{f}_{i-1}+U{x}_i+b_i\\ f_{i-1}& =f(a_i)\end{array}$$
为方便讨论，这里简化问题，令$$x_i=b_i=0$$，那么RNN的过程可以展开为
$$f(W...Wf(Wf(Wf())))$$
如果$$W$$中有某个数值大于1，而且使用不饱和的ReLU作为$$f(\cdot )$$，连乘后数值必定快速膨胀；
而饱和的sigmoid和tanh在这里可以约束数值的范围，避免这种膨胀现象的发生。
这个现象在CNN中不容易出现，原因是在CNN中连乘的$$W$$并不是相同的，而CNN权重往往具有很强的稀疏性。

2. 在RNN中，ReLU并不能解决梯度传递问题

依旧令$$x_i=b_i=0$$，考虑反向传播过程，展开后有
$$\frac{\partial f_3}{\partial W_1}=\frac{\partial f_3}{\partial a_3}{f}_2+\frac{\partial f_3}{\partial a_3}W\frac{\partial f_2}{\partial a_2}{f}_1+\frac{\partial f_3}{\partial a_3}W\frac{\partial f_2}{\partial a_2}W\frac{\partial f_1}{\partial a_1}\frac{\partial a_1}{\partial W_1}+...$$
只考虑第三项$$\frac{\partial f_3}{\partial a_3}W\frac{\partial f_2}{\partial a_2}W\frac{\partial f_1}{\partial a_1}\frac{\partial a_1}{\partial W_1}$$，在ReLU作用下有$$\frac{\partial f_3}{\partial a_3}=\frac{\partial f_2}{\partial a_2}=\frac{\partial f_3}{\partial a_1}=1$$，
但会发现，反向传播中依旧出现了$$W$$的连乘，这依旧很容易出现梯度消失和梯度爆炸（具体理由同1）；

3. 也存在一些在RNN成功使用ReLU的例子
   比如《A Simple Way to Initialize Recurrent Networks of Rectified Linear Units (2015)》提出的IRNN

批归一化

论文：《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift(2015)》

归一化&正则化&标准化

参考文章：《机器学习里的黑色艺术：normalization, standardization, regularization | 知乎, 刘锐》
归一化（Normalization）：数据预处理，将数据限定在特定范围内，消除量纲对建模的影响；
标准化（Standardization）：数据预处理，使数据符合标准正态分布；
正则化（Regularization）：在损失函数中添加惩罚项，增加建模模糊性，将建模关注点转移到整体趋势上；

具体操作

归一化的方式有很多种：

1. 最大最小值归一化 $$x^{\prime }=\frac{x-min}{max-min}$$
2. 对数归一化 $$x^{\prime }=\frac{lg(x)}{lg(max)}$$
3. 反正切归一化 $$x^{\prime }=\frac{2arctan(x)}{\pi }$$
4. 零平均归一化 $$x^{\prime }=\frac{x-mean}{std}$$

批归一化是在每层的激活函数之前添加一个BN操作，使得特征图数据归一化为均值为0，标准差为1的分布（不一定是正态分布）；并且在每一层中使用两个新的参数来调整输出的范围，以此来加强调整数据分布的能力，使得模型的每一层能够学习到适宜的表示范围；

对于某个mini-batch的输入，归一化的具体过程如下：
$$\begin{array}{rl}{x}^{(i)}& =\frac{x^{(i)}-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}\\ z^{(i)}& =\gamma x^{(i)}+\beta \end{array}$$
其中，
$${\mu }_B$$ 和 $${\sigma }_B$$ 分别是该mini-batch的平均数和方差；
$$ϵ$$ 是一个很小的数（通常取0.001），用于避免 $$\sigma =0$$ 导致分母为0的情况；
$$\gamma$$ 和 $$\beta$$ 分别是每一层中的两个新的参数，调整后的 $$x^{(i)}$$ 通过线性变化后得到归一化的 $$z^{(i)}$$ 输出

在预测阶段因为不再有mini-batch，所以直接使用在整个训练集的平均数、标准差进行计算即可；
所以在训练时每层会增加四个参数：$$\gamma ,\beta ,\mu ,\sigma$$ ，训练时采用移动平均的方式可以高效地获得在整个训练集各层的平均值和标准差；

在深度学习模型中，多数常规层在训练和预测过程中都表现出相同的行为，比如全连接层、卷积层、激活层等等。而BN层在训练阶段和预测阶段的行为是不完全一致的，这主要体现在均值$${\mu }_B$$和方差$${\sigma }_B$$上，

• 在训练阶段，$${\mu }_B$$和$${\sigma }_B$$都是根据当前特征图在线计算得到的，是一个动态的统计值；
• 在预测阶段，我们往往采用非常小的batch甚至只使用单样本，此时在线统计$${\mu }_B$$和$${\sigma }_B$$是不合理的。所以BN在训练过程中会通过移动平均（通常是指数平滑平均）统计每次训练的平均结果，最后将平均下来的$${\hat{\mu }}_B$$和$${\hat{\sigma }}_B$$作为预测阶段的均值和方差，它们是固定的统计值

效果

1. 可以很好的解决梯度爆炸和消失的问题，甚至饱和激活函数如sigmoid和tanh都可以在深度网络中正常使用；
2. 网络对权重初始化不再那么敏感。而且随机初始化可以在训练的开始显著减少梯度爆炸和消失的问题，但它不能保证训练过程中不再出现；
3. 可以使用更大的学习率，提高训练速度；
4. 具有正则化的效果，可以减少dropout等其他正则化技术的使用；
5. 缺点：BN操作增加了模型的复杂度，预测时间将不可避免地增加

但是多数情况下该缺点是可以忽略不计的，因为在训练完成后，BN层可以合并到前一层的卷积层或全连接层，在预测阶段不产生任何额外开销，具体参见《MobileNet-SSD网络解析 - BN层合并 | Hey~YaHei!》；但也有一些特殊的情况，比如二值量化、移位量化等网络在卷积、全连接的计算过程发生了变化，不能轻易将BN层融入

争论

参考：

• 《关于batch_normalization和正则化的一些问题？ - 论智的回答 | 知乎》
• 《Intro to Optimization in Deep Learning: Busting the Myth About Batch Normalization》==> 译文

事实上，BN的提出更多的是产生这样一个猜想，经过实现发现确实有效，又经过广泛的使用、实验，大家发现确实是个好东西，具体如何工作的也有不少人提出自己的解释和猜想，但至今没有一个广泛认可的解释。

提出者曾认为BN是降低了内部协变量偏移（指训练过程中，随着前一层参数的变化，本层的输入分布也随之发生的变化，称为Internal Covariate Shift, ICS）从而加速和稳定了训练过程。该观点后来被多次质疑，比如

1. 《How Does Batch Normalization Help Optimization? (No, It Is Not About Internal Covariate Shift) (2018)》就指出BN不仅没有降低ICS反而还增加了ICS，真正原因是因为BN使得损失平面更加平滑，容易收敛；
2. GAN之父Ian Goodfellow也曾猜想，深度学习实际有很多高阶的跨层交互，但因为算力受限，很少使用牛顿法等二阶以上的高阶优化。在梯度下降算法中，我们通常只用到了一阶优化，而忽略了高阶跨层交互带来的影响，每次更新一个层的权重后就会对后续层产生不利影响，而BN降低了这类影响——这一观点也能佐证最后一个全连接层加不加BN效果都差不多这一现象。

其他形式的归一化

• 特征归一化（Feature Normalization, FN）
  作用于网络最后一层的特征表示上（FN随后接的是目标函数层），用于提高习得特征的分辨能力；
  可用于人脸识别、行人重检测、车辆重检测等任务上；
  论文：《DeepVisage: Making face recognition simple yet with powerful generalization skills(2017)》
• 不同粒度的归一化
  有的时候使用BN是不合理的（比如训练时batch size太小），此时需要使用其他粒度的归一化，参考《详解深度学习中的Normalization，BN/LN/WN | 知乎, Juliuszh》

梯度裁剪

论文：《On the difficulty of training recurrent neural networks(2012)》
直接限制梯度的上限，简单粗暴，但却有效，这在RNN、强化学习等训练过程不稳定的任务中运用的比较多。

复用预训练层

迁移学习（Transfer Learning）在深度学习中相当常见，如果已经训练好了一个网络（比如可以识别猫），需要训练一个新的类似任务的网络（比如识别狗），可以直接使用已有网络的一部分浅层权重，重新初始化深层网络的权重来进行训练。

通常，深度学习模型浅层会提取一些底层的特征（比如颜色、点线），深层会提取一些抽象的特征（比如一些简单团、耳朵、鼻子等局部特征），所以输出最抽象也是最终的分类结果（一只猫/狗）。直观上理解，复用浅层特征就是复用浅层的特征提取能力，比如已经训练了一个可以识别猫的网络，那么它的浅层就会提取一些毛发之类的底层特征，恰好狗是有类似特征的，那么在训练狗的识别模型时复用一部分猫识别模型的浅层权重，相当于迁移了一部分基础能力过来，然后进行进一步的训练，来微调、融合这部分能力，训练出最终的目标——识别狗子的模型。

1. 加速训练过程
2. 有利于小样本任务的训练
3. 通常要求新网络的输入数据大小与复用网络的输入数据大小保持一致
4. 要求任务类型是相似的，具有类似浅层特征的，否则可能会有负面效果
5. 任务越接近，可以复用的浅层越多
6. 通常会在初期训练过程中固定复用层的权重，只训练随机初始化的权重；当训练比较稳定之后再同时微调（称为finetune）整个模型的权重

常见模型库

模型库通常称为model zoo

• tensorflow：https://github.com/tensorflow/models
• caffe：https://github.com/BVLC/caffe/wiki/Model-Zoo
• pytorch：https://github.com/pytorch/vision
• mxnet：https://github.com/dmlc/gluon-cv

无监督预训练

但实际操作中并不是总有类似任务的现成模型可以复用，甚至你的训练任务可能只有少量标注好的数据和大量未标注的数据，这时候有以下选择：

1. 继续标注数据
2. 如果标注繁琐或者成本过高，可以使用无监督预训练的方式

论文：《Why Does Unsupervised Pre-training Help Deep Learning?(2009)》

使用无监督训练，从底层开始逐层训练各个隐藏层，每次只训练一个层而固定其他层的权重；

无监督训练可以使用Restricted BoltzmannMachines (RBMs）、autoencoders等，目前autoencoders用的更多些；

最后用监督训练的方式，fine-tune较高的layers：

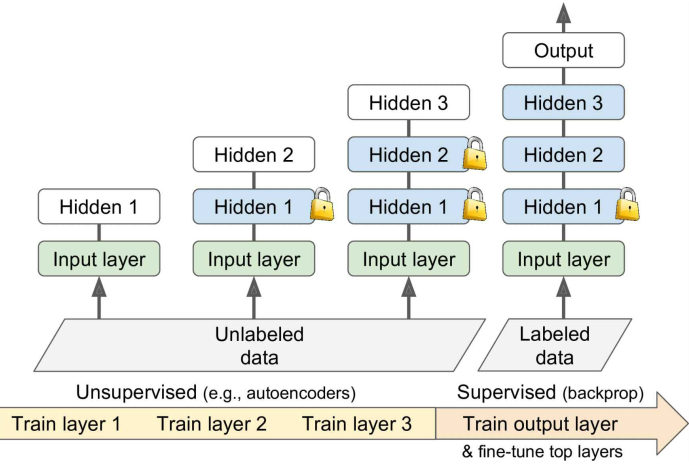
3. 寻找一个训练数据易收集且易标注的类似任务，先训练出一个模型来复用给这个任务
4. 在辅助任务上进行预训练，比如：
   • 想训练一个人脸识别的模型，为每一个注册者获取上百张人脸照片是不切实际的。

可以先获取大量随机人脸的照片，训练一个模型来检测两张人脸图片是否对应同一个人；

该任务得到一个比较好的特征检测器，复用该任务的底层权重，进而用少量数据来训练出特定人脸的识别模型

• 想为某个语言处理任务训练一个模型。

可以先获取大量的语句，训练一个分辨语法是否正确的模型。

（比如说把这些语句先都标记为good，然后打乱语序标记为bad进行训练）

该任务得到一个有一定语言能力的模型，复用该任务的底层权重，进而用少量数据来训练目标任务的模型

• Max Margin Learning，训练一个打分模型

SVM就是基于Max Margin Learning的一种分类器

为预测结果进行打分，用损失函数来训练一个模型，使得预测的好结果比坏结果的分数高于某个阈值